Суммирование погрешностей

Основы теории суммирования погрешностей.

Определение расчетным путем оценки результирующей погрешности по известным оценкам ее составляющих называется сумми­рованием погрешностей.

Главной проблемой, возникающей при суммировании, является то, что все составляющие погрешности должны рассматриваться как случайные величины. С точки зрения теории вероятностей они наиболее полно могут быть описаны своими законами распределе­ния, а их совместное действие — соответствующим многомерным распределением. Однако в такой постановке задача суммирования погрешностей практически не разрешима уже для нескольких со­ставляющих, не говоря о нескольких десятках.

Практически приемлемый путь решения данной задачи сумми­рования погрешностей состоит в отказе от определения и использо­вания многомерных функций распределения составляющих погреш­ности. Необходимо подобрать для характеристик составляющих такие числовые оценки (СКО, эксцесс и др.), оперируя с которыми можно было бы получить соответствующие числовые оценки ре­зультирующей погрешности. При этом следует учитывать, что:

• отдельные составляющие погрешности могут быть коррелированы между собой;

• при суммировании случайных величин их законы распределе­ния существенно деформируются, т.е. форма закона суммы может резко отличаться от формы закона распределения составляющих.

Правила суммирования погрешностей основываются на том, что погрешность по абсолютному значению всегда много меньше са­мой измеряемой величины. Поэтому изменение погрешности в зави­симости от изменения измеряемой величины может быть учтено, если все суммируемые случайные и систематические составляющие пог­решности разделить на аддитивные и мультипликативные. Сумма аддитивных составляющих даст значение аддитивной части результирующей погрешности, а сумма мультипликативных составляющих – значение мультипликативной части результирующей погрешности. В пределах некоторого диапазона изменения, как правило, десятикратного, измеряемой величины изменение результирующей погрешности может быть с достаточной степенью точности представлено прямой линией или простейшей кривой (парабола, гипербола). Это дает возможность описать результирующую погрешность линейной или нелинейной двузвенной формулой. При большем изменении измеряемой величины весь диапазон разбивается на участки, для которых и определяются крайние погрешности.

Для устранения влияния деформации формы законов распреде­ления все суммируемые составляющие исходно представляются своими СКО и все операции расчетного суммирования проводятся только над ними. Учет взаимных корреляционных связей между сумми­руемыми составляющими производится путем использования раз­личных правил суммирования для жестко и слабо коррелирован­ных составляющих. Эти правила рассмотрены далее.

В результате суммирования СКО составляющих получаются сред­ние квадратические отклонения соответственно аддитивной, муль­типликативной или нелинейной составляющих результирующей погрешности. СКО аддитивной составляющей результирующей пог­решности будет характеризовать результирующую погрешность вначале диапазона. Сумма СКО аддитивной и мультипликативной составляющих в конце диапазона описывает результирующую пог­решность в конце диапазона. Если участков несколько, то сумми­рование проводится на всех участках, а затем принимается реше­ние о методе описания результирующей погрешности.

Результирующую погрешность необходимо выразить в виде до­верительного интервала. Его расчет по полученному СКО является с точки зрения теории самой трудной операцией при суммировании погрешностей. Это связано с тем, что доверительный интервал равен произведению рассчитанного СКО и множителя, зависящего от закона распределения результирующей погрешности. В то же время вся излагаемая методика с самого начала была нацелена на то, чтобы обойтись без точного определения результирующего за­кона распределения суммы всех составляющих.

Практические правила расчетного суммирования результирую­щей погрешности состоят в следующем:

1. Для определения суммарного значения СКО должны учиты­ваться корреляционные связи различных составляющих погреш­ности. В связи с этим исходными данными для более точного рас­чета должны служить оценки именно всех отдельных составляющих погрешности, а не оценки некоторых суммарных погрешностей.

2. Для каждой составляющей должно быть найдено ее СКО. В большинстве случаев для этого необходимо знание или предпол­ожение о виде закона ее распределения.

3. Все суммируемые составляющие разделяются на аддитивные и мультипликативные составляющие, которые суммируются отдель­но.

4. Так как в большинстве случаев точное значение коэффициен­та корреляции р найти невозможно, то все погрешности должны быть условно разделены на:

• сильно коррелированные при 0,7 < |р| < 1, для которых счита­ют р = ±1 в зависимости от знака коэффициента корреляции;

• слабо коррелированные при 0 <= |р| <= 0,7, для которых р = 0.

5. Из суммируемых составляющих выделяются группы сильно коррелированных между собой погрешностей и внутри этих групп производится алгебраическое суммирование их оценок.

6. После алгебраического суммирования групп сильно коррели­рованных погрешностей суммарные по группам и оставшиеся вне групп погрешности можно считать некоррелированными и склады­вать по правилу геометрического суммирования.

Для определения СКО суммарной погрешности при начальном значении измеряемой величины складывают лишь аддитивные составляющие, а для определения СКО погрешности в конце диапазона изменения измеряемой величины — все просуммированные составляющие.

7. Для перехода от СКО погрешности к доверительному значению должно быть вынесено суждение о форме закона распределения результирующей погрешности и тем самым выбрано значение квантильного множителя.

Изложенная методика может быть несколько упрощена. Самым сложным в ней являются нахождение СКО всех составляющих по известным их интервальным оценкам и определение интервальной оценки результирующей погрешности по полученному СКО.

В обоих случаях необходимо знание закона распределения погрешностей. Упрощение методики суммирования состоит в том, чтобы сделать эти переходы по возможности более простыми. Один из вариантов состоит в следующем. Согласно центральной предельной теореме, если число суммируемых независимых составляющих до­статочно велико (практически при m >= 5) и если среди этих состав­ляющих нет существенно преобладающих над остальными, то ре­зультирующий закон распределения близок к нормальному. Однако предположение о близости закона распределения к нормальному без соответствующего анализа достаточно рискованно даже и при боль­шом числе суммируемых составляющих. Тем не менее при недо­статке времени и невысоких требованиях к точности получаемого результата предположение о нормальности закона распределения результирующей погрешности вполне возможно. В этом случае до­верительный интервал Δ = ZpS_∑, где Z_P — квантильный множитель, определяемый через функцию Лапласа; S - суммарное СКО или его оценка.

Такой прием существенно снижает трудоемкость расчетов, но может вносить весьма значительные ошибки, если реальное рас­пределение сильно отличается от нормального закона. Например, при фактическом арксинусоидальном распределении ошибка мо­жет достигать 180%. Поэтому использовать его надо весьма ос­мотрительно.

В качестве другого пути упрощения перехода от СКО результи­рующей погрешности к ее интервальной оценке следует указать воз­можность использования доверительной вероятности Р_д = 0,9, при которой для большой группы различных распределений имеет мес­то соотношение

Δ = l,6S_∑

Действительно, для широкого класса симметричных, высокоэнтропийных (k > 1,7) распределений, а именно для равномерного, треугольного, трапецеидальных, нормального, экспоненциальных с показателем степени α >= 2/3, двухмодальных с глубиной антимодальности менее 1,5, интегральные кривые F(x) в области 0,05 и 0,95 квантилей пересекаются между собой в очень узком интервале значений X/S = 1,6 ± 0,05. Поэтому с погрешностью 0,05S можно читать, что квантили 0,05 и 0,95 для любых из этих распределений могут быть, найдены как

Х₀,₀₅ = Х_ц - 1,6S и Х₀,₉₅ = Х_ц + 1,6S, где Xц - координата центра распределения; ST— его СКО. Отсюда следует, что значение доверительного интервала, найденное по формуле выше, для любого из названных распределений является интервалом с 90%-ной доверительной вероятностью.

При Р_д > 0,9 интегральные кривые для разных законов рас­пределения резко расходятся между собой. В этом случае для нахождения доверительного интервала Δ = ZpS_∑ предложено вместо большого числа таблиц квантилей разнообразных распре­делений найти для близких классов распределений аппроксими­рующие выражения Z_p = f(ε,P), где ε — эксцесс распределения.

Для входящих в классы экспоненциальных и трапецеидальных распределений, а именно: распределения Лапласа (ε = 6); нормаль­ного распределения (ε = 3); трапецеидального распределения с соот­ношением верхнего и нижнего оснований 1:2 (ε = 2) и равномерного распределения (ε = 1,8), зависимость квантильного множителя от эксцесса и доверительной вероятности аппроксимируется уравнением

Zp =1,62 [3,8 (ε-1,6)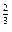]^{lglg[1/(1-p)]}

Погрешность аппроксимации не превышает 4% при изменении Р от 0,9 до 0,99 и 8% — от 0,9 до 0,999.

Для кругловершинных двухмодальных распределений, представ­ляющих собой композицию нормального и дискретного двузначного распределений, в диапазоне изменения е от 3 до 1,3 для Р от 0,9 до 0.999 с погрешностью 10% зависимость Z_p = f(ε,P) аппроксимирует­ся выражением

Z_p = 1,6{3,6[1 + lg(e-1)]}^{lglg[1/(1-p)]}

Для островершинных двухмодальных распределений, образующихся как композиция распределения Лапласа и дискретного двузначного распределения, рассматриваемая зависимость в интервале значений ε от 1,8 до 6 при Р от 0,9 до 0,999 с погрешностью 5% аппроксимируется формулой

Z_p = 1,23[1+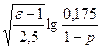

Для уплощенных распределений, образующихся как компози­ция экспоненциального распределения с α =1/2 и равномерного рас­пределения в интервале значений ε от 6 до 1,8 с погрешностью 8%, рассматриваемая зависимость аппроксимируется формулой

Z_p = 1,56 [1,12 + (ε - 1,8)^0,58 / √10]^{lg[0,1/(1-p)]}

Использование приведенных уравнений позволяет, не прибегая к таблицам, с достаточной для практики степенью точности вычис­лять доверительные интервалы для всех встречающихся распреде­лений погрешностей. Однако для выбора формулы нужно вынести суждение о классе распределения суммарной погрешности.

Дальнейшие упрощения методики, выражающиеся в пренебре­жении разделением погрешностей на аддитивные и мультиплика­тивные, коррелированные и некоррелированные, недопустимы, пос­кольку при суммировании погрешностей получены неверные результаты.

Дата добавления: 2014-01-20