Уравнение метода

Тема 11. Достаточные условия оптимальности.

В ТОУ для решения задач применяется специфический математический аппарат, основанный на достаточных условиях оптимальности. Это утверждает, что если утверждаемое условие оптимальности достаточно, то данный управляемый процесс оптимальный. Но это не означает, что не может быть других оптимальных процессов, для которых достаточные условия не выполняются. Другими словами, условие А достаточно для выполнения заданного условия В.

Тема 12. Метод Лагранжа – Понтрягина для непрерывных управляемых процессов.

Теоретической основой всех рассматриваемых вычислительных методов ТОУ являются ДУО. Эти условия проявляются как признак оптимальности применительно к непрерывным и дискретным управляемым процессам (x*, u*) в общем виде. Ставя при формулировке задач ТОУ ряд дополнительных ограничений на постановку задачи, получаем соотношения в форме Лагранжа – Понтрягина как необходимые условия оптимальности, которые вытекают из теоремы ДУО, отвечая необходимым условиям выполнения этих достаточных условий. Применительно к непрерывным управляемым процессам они известны в виде принципа максимума Понтрягина.

Рассмотрим задачу ТОУ для непрерывной системы: пусть заданы ДУ процесса

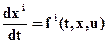i= 1, …, n (5)

x=(x¹, x², …, xⁿ)

u=(u¹, u², …, u^r),

где x – n – мерный вектор её состояния

u – r – мерный вектор управления.

На управление может быть наложено ограничение uÎV^t

Где V^tÎR^t – некоторая область возможных значений управления (R – множество действительных чисел, векторов), которая может изменяться во времени

Для ДУ (5) будем считать заданное начальное состояние системы в виде совокупности условий

xⁱ(0)=x_{i 0}, i=1, 2, …, n

кроме того, может быть задано состояние системы в конечный момент времени t=T

xⁱ(T)=x_{i 1}, i=1, 2, …, m, m£n (6)

представляющее дополнительные ограничения на протекающий в ней процесс (x(t), u(t)). Ограничения (6) могут быть заданы не по всем переменным, а лишь по некоторой их части, в данном случае по первым m.

Будем считать, что качество процесса оценивается функционалом

(7)

Если правый конец траектории процесса зафиксирован с помощью соотношений (6), то второе слагаемое в (7) является постоянной величиной и не влияет на нахождение оптимального решения.

Требуется определить процесс (x*(t), u*(t)), удовлетворяющий условиям (5, 6) и минимизирующий функционал. Такой процесс называется оптимальным.

Пусть (x*(t), u*(t)) – допустимый процесс, удовлетворяющий теореме о достаточных условиях оптимальности. Это означает что существует функция 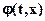, обладающая тем же свойством, что и выражение

(8)

Достигается при tÎ[0;T] максимума по переменным x, u в точке (x*(t), u*(t)), а функция Ф(х)=j(T, x) + F(x) принимает максимальное значение при х=х*(Т)

Этот процесс удовлетворяет достаточным условиям.

{При рассмотрении непрерывных систем, для формулировки теории вводятся 2 функции (R(t,x,u) и Ф(х), а для их построения вводятся функции j(х) (не требует ни каких свойств типа непрерывности и дифференцируемости) переменных (t, x¹, x², …, xⁿ) }

Для рассмотрения метода введём функцию Гамильтона:

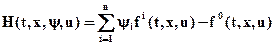
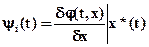i=1, 2, …, n,

где 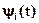- вектор функция,

(x*(t)) означает, что после вычисления вектор х должен принимать значение (x*(t)).

С помощью функции Гамильтона функция может быть записана в виде

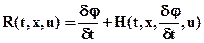(9)

Так как процесс (x*(t), u*(t)) удовлетворяет достаточным условиям оптимальности то

R(t, x*(t), u*(t))³R(t, x, u)

Для всех (x,u)ÎV^t, отсюда вытекает, что неравенство

R(t, x*(t), u*(t))³R(t, x(t), u)

выполняется для всех допустимых значений управления uÎV^t

Сравнивая полученные неравенство с (9) получаем в качестве следствия (т.к. слагаемое 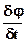не зависит от u), что

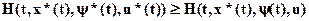
Это неравенство говорит о том что выражение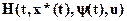, рассматриваемое при каждом фиксированном значении tÎ[0;T] как функция от u, достигает максимального значения при u=u*(t). Это обстоятельство может быть выражено в следующей форме.

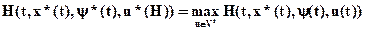(10)

Дата добавления: 2014-01-20