Предельные теоремы. Сейчас нас будут интересовать закон распределения и некоторые связанные с ним числовые характеристики суммы случайных величин при условии

Сейчас нас будут интересовать закон распределения и некоторые связанные с ним числовые характеристики суммы случайных величин при условии, что распределение и числовые характеристики слагаемых известны, а их число неограниченно возрастает.

Неравенство Чебышева (приводится без доказательства). Для произвольной случайной величины x с математическим ожиданием a = M (x)и дисперсией s 2= D (x)для любого e > 0 справедливо неравенство

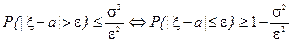. (2.22)

Из неравенства Чебышева следует: чем меньше дисперсия, тем меньше вероятность отклонения случайной величины от своего математического ожидания более чем на e.

Теорема Чебышева (приводится без доказательства). Пусть { x n} - последовательность независимых одинаково распределенных случайных величин, имеющих конечные дисперсии. Тогда вероятность отклонения их среднего арифметического от их математического ожидания по модулю меньше чем на e стремится к 1 при неограниченном увеличении n.

(2.23)

В этом случае говорят, что среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому математических ожиданий слагаемых.

Пример. Обычно при определении численного значения некоторой постоянной величины проводится несколько измерений и в качестве искомого значения принимается их среднее арифметическое. Действительно, результат каждого измерения можно рассматривать как случайные величины x1,..., xn. Если результаты измерений независимы, имеют одно и то же математическое ожидание и их дисперсии ограничены одной и той же константой (что на практике обычно выполняется), то согласно теореме Чебышева среднее арифметическое сходится по вероятности к 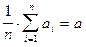(истинному значению измеряемой величины).

Теорема Бернулли (следствие теоремы Чебышева). Эта теорема устанавливает связь между относительной частотой события n(A) и его вероятностью p (A). Пусть производится n независимых, однородных испытаний (схема Бернулли), в каждом из которых событие А может произойти с вероятностью p (A)=р. Введём в рассмотрение случайные величины x₁,..., x_n- индикаторы испытаний. Напомним, что x_iпринимает только два значения: a) 1, если в i -м испытании событие A наступило, b) 0 в противоположном случае. Ранее были найдены M(x_i) = p и D(x_i) = pq. Последовательность случайных величин {x_i} удовлетворяет условиям теоремы Чебышева и поэтому

Остаётся отметить, что сумма 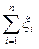равна числу появлений события A при n испытаниях, а значит, является относительной частотой, которую ранее обозначали через n(A).

Таким образом, при неограниченном увеличении числа испытаний относительная частота n (A) события A сходится по вероятности к P(A) - вероятности его появления при одном испытании. Это утверждение и является теоремой Бернулли.

Дата добавления: 2014-01-20