
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Экспоненциальная кривая
|
|
|
|
0 2 4 6 8 10 12 14 16 18 20
Рисунок 2 - Кривая роста биомассы дрожжевых клеток
Отношение (1.9) характеризует чувствительность вида к нехватке пищи. Во-первых, если дробь ε/γ мала, то вид очень чувствителен к нехватке пищи. Во-вторых, из (1.8) следует, что при малых N0 и конечном t имеем
.
N 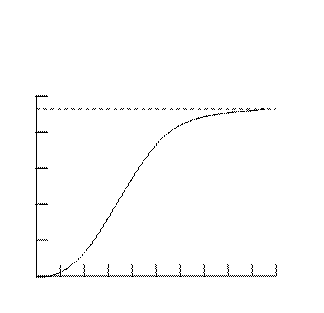
K
Рис. Рисунок 3 - Логистическая модель с емкостью среды К= ε/γ
В популяции малой численности (когда отсутствует заметное влияние лимитирующих факторов), кривая изменения численности сходна с кривой динамики роста (1.3) в отсутствие лимитирующих факторов среды.
Широкое использование уравнения (1.7) связано с тем, что оно хорошо отражает начальный экспоненциальный рост популяции и асимптотическое установление ее численности к некоторому конечному значению, т.е. это простейшее дифференциальное уравнение, которое обладает следующими свойствами (рис.3):
1. при малых значениях N, пока популяция не исчерпала свои ресурсы (пищу или пространство), логистическое уравнение (1.7) сводится к уравнению (1.1), и возрастание N носит экспоненциальный характер;
2. с возрастанием t растет N, ресурсы популяции уменьшаются, рост постепенно замедляется (фаза отрицательного ускорения), и N постепенно приближается к постоянному значению К= ε / γ.
Обобщая модель (1.7), будем называть обобщенной логистической популяцией любую популяцию, локальный закон роста которой описывается уравнением
dN = F (N), (1.10)
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 985; Нарушение авторских прав?; Мы поможем в написании вашей работы!