Простейшие типы дифференциальных уравнений первого порядка

1) Уравнение с разделёнными переменными

или

.

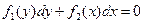Решая первое уравнение, получим .

Интегрируя, найдём общее решение .

Решая второе, получим .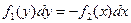

Интегрируя, найдём общее решение.

2) Уравнение с разделяющимися переменными,

или

.

Разделим обе части первого уравнения 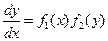на и умножим на , получим уравнение с разделёнными переменными

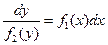
Для второго уравнения: разделим обе части на произведение 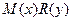, получим также уравнение с разделёнными переменными

.

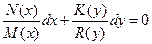Операция деления уравнения на произведение 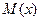называется разделением переменных.

При делении на произведение 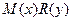можно потерять некоторые решения, которые получаются из уравнения

.

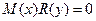Определяя из этого уравнения решения 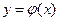, следует проверить, является ли оно решением исходного уравнения. Если не является, его следует отбросить, а если является, то проверить, входит ли оно в общий интеграл. Если входит, то оно есть частное решение, а если не входит, то это решение называется особым.

Пример 17 Решить уравнение .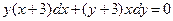

Решение:

Разделим уравнение на произведение , получим:

.

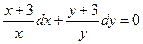Интегрируя, получим общий интеграл:

.

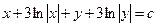
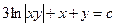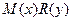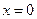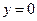В этом уравнении имеет вид . Его решение , является решением исходного уравнения, но не входит в общий интеграл. Следовательно, решение 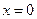, 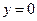является особым.

Пример 18 Найти общее решение .

Решение:

;

;

интегрируя, найдем общее решение

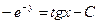или ;

;

;

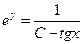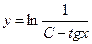3) Однородные уравнения.

Функция 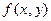называется однородной степени , если для любых и выполняется равенство

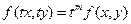
Если функци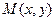и и 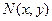однородные одной и той же степени , то дифференциальное уравнение называется однородным.

Однородное уравнение всегда можно привести к виду

,

решается подстановкой:

или ; .

Пример 19 Решить .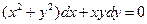

Решение:

Данное уравнение является однородным, т.е. функции 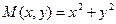, 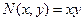однородные степени 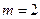. Сделаем замену Тогда уравнение перепишется так:

;

;

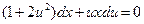разделяя переменные, получим:

;

;

;

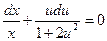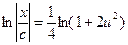Так как у нас 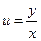, то , , .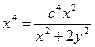

Дата добавления: 2014-01-11