Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Лекция16

Однородное дифференциальное уравнение второго порядка имеет вид

,

где – числа, .

Если функции 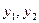образуют фундаментальную систему решений, то общее решение дифференциального уравнения имеет вид:

.

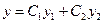Предположим, что частные решения имеют вид:

.

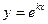Найдём производные:

,

и подставим в исходное дифференциальное уравнение

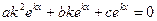
или

,

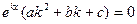т.к. 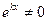, то

.

Данное уравнение называется характеристическим уравнением.

При решении квадратного уравнения возможны три случая:

1) , различные действительные корни, если дискриминант . Фундаментальную систему решений составляют функции:

,

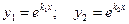общее решение имеет вид:

.

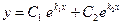2) корни действительные, равные, 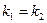, если дискриминант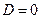. Фундаментальную систему решений составляют функции:

,

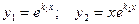общее решение имеет вид:

.

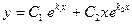3) корни комплексные числа, , если дискриминант . Фундаментальную систему решений составляют функции:

,

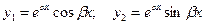общее решение имеет вид:

.

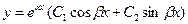Пример 26 Решить

а) ; б) ; в) .

Решение:

а) составим характеристическое уравнение:

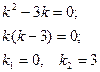
общее решение имеет вид:

или

.

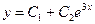б) составим характеристическое уравнение:

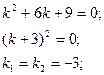
общее решение имеет вид:

.

в) составим характеристическое уравнение:

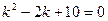
, где .

Итак, 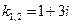, комплексные числа, где .

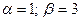общее решение имеет вид:

.

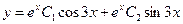16.1 Линейные неоднородные дифференциальные уравнения.. Метод Лагранжа

Рассмотрим линейное неоднородное дифференциальное уравнение

где непрерывная функция. Однородное уравнение соответствующее неоднородному уравнению будет

Справедлива следующая теорема о структуре общего решения линейного неоднородного дифференциального уравнения:

Если 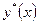– частное решение уравнения

а 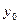– общее решение однородного уравнения то общее решение неоднородного уравнения равно сумме частного решения неоднородного уравнения и общего решения однородного уравнения

Замечание.

Если правая часть уравнения есть сумма нескольких функций 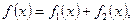, то частное решение уравнения равно сумме частных решений, отвечающих каждой функции в отдельности .

Как мы убедились раньше, задача отыскания общего решения неоднородного уравнения сводится к отысканию общего решения однородного уравнения и частного решения неоднородного уравнения .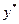

Приведем метод, позволяющий определить общее решение неоднородного уравнении по общему решению однородного уравнения.

Метод Лагранжа (метод вариации постоянных) решения линейного неоднородного дифференциального уравнения второго порядка

Алгоритм метода:

1. Решить однородное уравнение

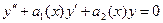
и записать его общее решение

2. Записать общее решение неоднородного уравнения, полагая произвольные константы функциями от x:

,

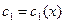
тогда

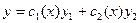
3. Записать систему уравнений

и решить ее.

4. Полученное решение подставить в .

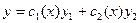Пример 27 Решить уравнение

Решение:

Для соответствующего однородного уравнения 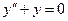общее решение имеет вид

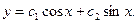
Запишем его в виде

составляем систему

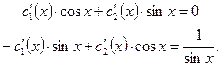
Решаем эту систему по методу Крамера:

,

где

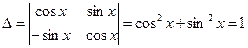
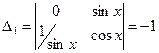
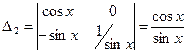
получим

Интегрируя, найдем

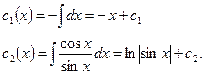
Подставляя найденные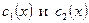

в общее решение однородного дифференциального уравнения

,

получим

.

Дата добавления: 2014-01-11