Лекция №1 Рекуррентные последовательности

КОМПОНЕНТЫ ТЕОРИИ ЛИЧНОСТИ

Теории личности в зарубежной психологии

Психология личности интересуется индивидуальными различиями и целостной индивидуальностью, стараясь понять, каким образом различные аспекты функционирования индивида связаны между собой.

Теория – это система взаимосвязанных идей, построений и принципов, имеющая своей целью объяснение определенных наблюдений над реальностью. Теории личности – это тщательно выверенные умозаключения или гипотезы о том, что представляют собой люди, как они себя ведут и почему они поступают именно так, а не иначе.

Теории выполняют две основные функции: они объясняют и предсказывают поведение.

1. Теория личности представляет поведение как определенным образом организованное, благодаря чему оно становится понятным.

2. Теория должна предсказывать будущие события. Она должна обеспечивать основу для прогнозирования результатов и событий, которые пока еще не наступили.

1) структура — базовые элементы, или строительные блоки, личности; Относительно неизменные характеристики, которые люди демонстрируют в различных обстоятельствах и в разное время

2) процесс — динамические аспекты личности, включая мотивы; Почему люди поступают так, а не иначе.

3) рост и развитие — как мы развиваемся в уникальные личности, которыми все мы являемся; Детерминанты, определяющие развитие личности (генетические и средовые)

4) психопатология — природа и причины нарушений в нормальном функционировании личности;

5) изменение — как люди меняются и почему они иногда сопротивляются изменениям или вообще не способны меняться.

В науке о личности сложилось семь теорий личности. Выделяют психодинамическую, аналитическую, гуманистическую, когнитивную, поведенческую, деятельностную и диспозитивную теории личности.

Определение. Последовательность u ₁, u ₂, …, u_n, … элементов поля P называется рекуррентной (возвратной) последовательностью порядка k, если её члены удовлетворяют равенству (рекуррентному соотношению) (1). Здесь и далее в тексте n принимает значения во множестве N натуральных чисел.

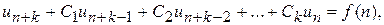(1)

где k – фиксированное натуральное число, называемое порядком рекуррентности, C_i – фиксированные элементы поля P, называемые коэффициентами рекуррентного соотношения, f (n) – некоторая функция, натурального аргумента, принимающая значения в поле Р.

Последовательность { u_n }, члены которой удовлетворяют соотношению (1), называется решением соотношения (1). Рассмотрим примеры рекуррентных последовательностей над полем R действительных чисел.

Примеры. 1. Последовательность Фибоначчи – рекуррентная второго порядка, определяется соотношением u_{n +2} = u_{n +1} + u_n, и ₁ = и ₂ = 1. Члены этой последовательности 1, 1, 2, 3, 5, 8, 13, … называются числами Фибоначчи.

2. Геометрическая прогрессия - рекуррентная последовательность первого порядка, её члены удовлетворяют соотношению b_{n +1} = qb_n, q - знаменатель прогрессии.

3. Арифметическая прогрессия - рекуррентная последовательность первого порядка: a_{n +1} = a_n + d, d - разность прогрессии.

Определение. Рекуррентная последовательность { u_n } называется однородной порядка k (k Î N), если её члены удовлетворяют соотношению:

u_n+k + С ₁ u_n+k-1 +…+ С_k u_n =0, (2)

где С_i - произвольные постоянные из поля Р.

Свойство 1. Сумма решений рекуррентного соотношения (2) является решением соотношения (2).

Свойство 2. Произведение решения рекуррентного соотношения (2) на элемент поля Р является решением соотношения (2).

Следствие. Множество решений соотношения (2) относительно операций сложения решений и умножения решений на скаляры из поля Р образует векторное пространство над полем Р.

Определение. Система последовательностей { a_n ¹}, { a_n ²}, …, { a_n ^s}, заданных в поле Р, называется линейно независимой, если из тождеств относительно n:

a ₁ a_n ¹ + a₂ a_n ² + … + a_s a_n^s = 0, a_i - скаляры из Р,

следует, что a ₁ = a ₂ = … = a _s = 0.

Найдем частное решение соотношения (2) в виде геометрической прогрессии lⁿ. Подставим в (2) данное решение. Получим уравнение относительно l, называемое характеристическим уравнением

l^k + C ₁ l^{k -1} + … + C_k = 0

данного рекуррентного соотношения. Это уравнение имеет не более k корней над полем Р. Пусть l ₁, l ₂, …, l_k – корни характеристического уравнения. Возможны следующие случаи.

I. Все корни попарно различны, и их число равно k. Тогда общее решение соотношения (2) записывается в следующем виде:

a_n = a ₁ l ₁ ⁿ + a ₂ l ₂ ⁿ + … + a_k l _kⁿ, a_i Î P.

II. Среди корней есть кратные. Пусть l _i – корень кратности s, тогда общее решение соотношения (2) имеет вид:

a_n = a ₁ l ₁ ⁿ + a ₂ l ₂ ⁿ + … + (a_{i 0} + a_{i 1} n + …+ a_{is -1} n^{s -1}) l_i ⁿ + …+ a_k l _kⁿ, a_i Î P.

Пример. Найти общий член последовательности Фибоначчи над R:

u_{n +2} = u_{n +1} + u_n, n Î N, u ₁ = u ₂ = 1.

Решение. Составим характеристическое уравнение, соответствующее данному однородному соотношению:

,

его корни 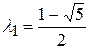, различны, тогда общий член последовательности Фибоначчи запишется так: . Для вычисления постоянных a ₁, a ₂ воспользуемся начальными условиями: u ₁ = u ₂ = 1. Для п = 1 и п = 2 составим и решим систему линейных уравнений:

Получим окончательно, что общий член последовательности Фибоначчи над полем действительных чисел имеет вид:

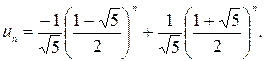
Дата добавления: 2014-01-20