Параметров модели (МНК)

ЛЕКЦИЯ 1. ПОСТРОЕНИЕ МОДЕЛИ: ОПРЕДЕЛЕНИЕ

Вернемся к первому этапу. После формирования гипотезы о виде зависимости (функционального вида правой части уравнения регрессии) необходимо выполнить определение входящих в уравнение коэффициентов – подбор параметров зависимости - и тем самым установить окончательно модель явления. Это осуществляется методом наименьших квадратов (МНК). Получающаяся модель проверяется на значимость с помощью различных критериев, представляющих основу статистической проверки гипотез, например, если

y_i = f(x_i) + ε_i, где f(x_i)=a_o + a₁x (1.2)

то коэффициенты определяются по МНК условием обращения в минимум функции

∑(y_i-a_o-a₁x)²→min, (1.3)

где требование минимизации квадратов отклонений приводит к системе нормальных уравнений (линейные алгебраические уравнения особого вида) для нахождения из нее коэффициентов a_i.

В экономике и, следовательно, в эконометрике исследуемые явления и характеризующие их величины это сложные случайные процессы и случайные величины, параметры этих процессов. Случайные величины в процессе анализа представляются состоящими из постоянной компоненты и случайной компоненты. При этом постоянная составляющая это математическое ожидание, или среднее арифметическое (среднее) значение исходной случайной величины:

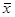= (1.4)

Если же данные не сгруппированы, то все частоты f равны 1 и получаем формулу простого среднего:

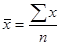(1.5)

Среднее случайной компоненты, или остатка равно нулю. Если бы это оказалось не так, то это ненулевое значение следовало бы включить в среднее значение исходной случайной величины и, таким образом, все свелось бы к предыдущему. Мера разброса (вариации) случайной величины, или, что то же, ее распределения, - это дисперсия.

Первоначально дисперсия определяется как среднее квадрата разности между самой случайной величиной и средним этой случайной величины:

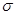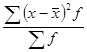Var(χ) = ² = (1.6)

В этом выражении коэффициенты ƒ не что иное как веса, или весовые коэффициенты значений величины χ. Это попросту величины, показывающие сколько раз входят те или иные значения в данное эмпирическое распределение величины χ для дискретных распределений или же в данный интервал (данную группу) для непрерывных распределений.

Часто при расчетах используют выражение для дисперсии в виде разности среднего от квадрата исходной случайной величины и квадрата среднего от нее:

σ² = - 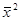(1.7)

Тогда окончательно для дисперсии исходной случайной величины получаем, что она равна дисперсии остатка, поскольку вся вариация исходной случайной величины равна вариации остатка, просто по самому определению остатка.

В действительности, кроме самых простых и редких случаев, неизвестно распределение случайной величины и даже основные характеристики изучаемой генеральной совокупности. Требуется получить информацию о случайной величине, характеризующей данное явление или процесс или соответственно генеральной совокупности, из результатов наблюдений. Совокупность результатов наблюдений представляет собой выборку из генеральной совокупности и по этим данным (выборки) с применением подходящей формулы и методов оценивания (прежде всего метода наименьших квадратов) получают приближенное значение неизвестной характеристики (параметра) исследуемой случайной величины или в терминах статистики генеральной совокупности.

Эконометрика использует для изучения различных явлений и процессов признаки, характеризующие эти явления и процессы. Признаки могут быть количественными и атрибутивными, не поддающимися непосредственно количественному измерению. Эконометрика сосредоточена преимущественно на исследовании явлений и процессов, характеризующихся количественными признаками. Тем не менее, она способна исследовать и взаимосвязи между атрибутивными (не количественными) признаками. Сами количественные признаки это фактически случайные величины, которые описываются своими распределениями (совокупностью принимаемых значений и совокупностью вероятностей, с которыми эти значения принимаются). Соответственно для признаков определяются средние, а сами случайные величины могут быть представлены в виде суммы средней и остатка, характеризующего случайные флуктуации.

у = + ε, (1.8)

где средняя (первое слагаемое) может быть приближена или просто заменена некоторой функцией, например линейной:

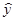= a_o + a₁x (1.9)

Это представление имеет глубокий смысл и будет неоднократно использоваться и обсуждаться далее. Далее помимо среднего для признака как для случайной величины определяется дисперсия, которая служит мерой вариации признака в целом (интегральная характеристика колеблемости признака).

D=σ²= (1.10)

Эконометрика исследует взаимозависимости между признаками и динамику их изменения во времени. Признаки, зависящие от других называются зависимыми, или объясняющими. Признаки от которых зависят первые (зависимые) называются независимыми, или факторами, или регрессорами. Далее мы увидим, что их так называемая независимость друг от друга отнюдь не носит абсолютный характер. Тем не менее понятие независимости факторов является весьма важным и весьма полезным начальным предположением. После исследования соответствующих базовых моделей начального уровня удается строить и изучать более сложные и более совершенные модели, в которых возможно учитывать частичную зависимость факторов.

Также естественно, что в качестве начальных базовых моделей используются простейшие зависимости, например линейные. После этого рассматривают модели, которые можно преобразовать к линейным. И наконец, только после этого существенно нелинейные модели. О том, каков точный смысл этих понятий речь пойдет в следующих лекциях.

Прежде всего, необходимо определить остаток (иначе отклонения, или погрешности) для каждого конкретного наблюдения. Этот остаток после принятия гипотезы линейной зависимости определяется как разность между фактическим значением наблюденной зависимой величины у и ее расчетным значением, получаемым по значению фактора х и формуле линейной зависимости у от х.

Линия графика (линейной зависимости), или линия регрессии должна быть такова, чтобы указанные остатки являлись минимальными. Как понимать требование минимальности именно всех остатков? Ведь уменьшая одни остатки, мы всегда с необходимостью будем увеличивать другие. Наилучший способ это потребовать минимизации суммы квадратов остатков. Остатки еще называют отклонения. В этом случае говорят о минимизации суммы квадратов отклонений. Это одно и то же. Наилучшее соответствие кривой точкам наблюдений получилось бы в предельном случае абсолютно точного соответствия, когда кривая (в нашем случае прямая) пройдет точно через все точки. Но это нереально для линии регрессии, ввиду наличия случайного члена и ошибок наблюдений.

Именно описанный только что принцип минимизации квадратов остатков и его реализация называются методом наименьших квадратов (МНК). Поскольку существует также модификация и развитие его, то говорят также о традиционном, или обычном МНК. В математике (математической статистике и теории приближенных вычислений) МНК рассматривается в качестве одного из наиболее важных и эффективных методов приближенных вычислений и методов оценивания. По существу именно ситуации, когда система алгебраических линейных уравнений не имеет точного решения, является наиболее общей и важной с практической точки зрения. И в большинстве случаев удается найти содержательные приближенные решения, дающие ответ на вопросы, поставленные в данной задаче.

Важно понимать, что в МНК переменные и коэффициенты как бы меняются местами. Из требования минимизации суммы квадратов остатков вытекает довольно простая система линейных алгебраических уравнений. Она называется нормальная система, или система нормальных уравнений. В этой системе уравнений в качестве известных величин выступают величины, получаемые в результате перемножения, возведения в квадрат и последующего суммирования наблюденных значений переменных. Надо отчетливо понимать, что, несмотря на свой нередко относительно громоздкий вид, это всего лишь известные величины, играющие теперь роль коэффициентов системы. С другой стороны сами исходные коэффициенты линейной зависимости (параметры) неизвестны. Именно их и надо определить из системы нормальных уравнений.

Для решения системы алгебраических линейных уравнений существуют различные методы от простого исключения переменных до использования определителей и обратных матриц, метод Гаусса, систематизирующий и обобщающий исключение переменных и называемый поэтому методом последовательного исключения неизвестных. Для случая двух переменных эти формулы нахождения решения системы нормальных уравнений довольно просты. Для множественной регрессии, когда рассматриваются зависимости от множества факторов такие формулы становятся более громоздкими.

Важно то, что в очень большом количестве исследуемых ситуаций выборочная дисперсия весьма близка к генеральной дисперсии и является хорошим приближением и тем самым хорошей оценкой для генеральной дисперсии, кроме отдельных специальных случаев. В то же время выборочное среднее не является достаточно хорошей оценкой, а служит всего лишь грубым первоначальным приближением к оценке генерального среднего, которое уточняется с помощью формул, использующих выборочную дисперсию.

Итак, оценки – это приближения к неизвестным величинам с некоторыми важными хорошими свойствами. Опираясь на оценки важнейших характеристик случайных величин, выявляют и исследуют связи между ними, определяют величину этих связей, исходя из важнейших показателей, характеризующих статистические зависимости между величинами и процессами. Мерой взаимосвязи между переменными является выборочная ковариация, которая для последовательности наблюдений двух переменных представляет среднее произведений разностей результатов наблюдений и их соответствующих средних. Есть другая форма вычисления ковариации, когда она представляется в виде среднего попарных произведений соответствующих результатов наблюдений этих двух переменных, из которого вычитается произведение средних этих двух переменных:

Cov(x,y)=å(x-`x)(y-`y)/n=[(∑xy)/n] – [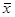] (1.11)

Ковариация легко вычисляется, но при всей ее простоте она вовсе не является наилучшим измерителем взаимосвязи между величинами. Более точно характеризует зависимость коэффициент корреляции. Выборочный коэффициент корреляции, или просто выборочная корреляция это просто частное от деления выборочной ковариации на произведение выборочных дисперсий соответствующих переменных. Преимущество коэффициента корреляции перед ковариацией заключается в том, что ковариация зависит от единиц, в которых измеряются переменные, коэффициент корреляции это величина безразмерная.

r=Cov(x,y)/Övar(x)var(y) (1.12)

Дата добавления: 2014-01-20