Геометрический смысл частных производных функции двух переменных

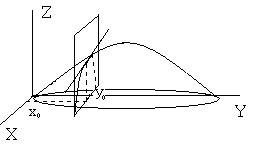
Пусть 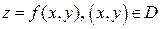, – функция двух переменных. Графическим изображением этой функции является поверхность над областью 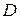. Рассмотрим точку 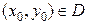, в которой данная функция имеет конечные частные производные 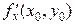и .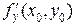

Пересечением плоскости 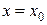с заданной поверхностью является кривая. Аппликата этой кривой определяется по формуле 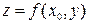. Частная производная 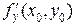является тангенсом угла наклона касательной к полученной кривой 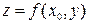, лежащей в плоскости 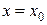, с положительным направлением оси OY в точке 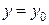. Направляющий вектор этой касательной имеет координаты .

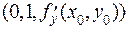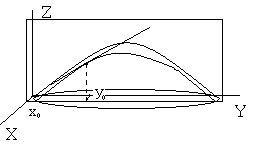
Пересечением плоскости 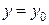с заданной поверхностью является кривая. Аппликата этой кривой определяется по формуле 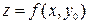. Частная производная 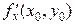является тангенсом угла наклона касательной к полученной кривой 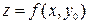, лежащей в плоскости 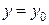, с положительным направлением оси OX в точке 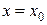. Направляющий вектор этой касательной имеет координаты .

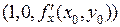При исследовании функций нескольких переменных приходится брать производные высших порядков по различным переменным. Например, символ 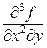означает, что у функции взята производная по переменной 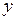и от нее – дважды производная по 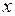. Эта же производная может быть записана как 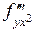. Такие производные можно также брать с применением пакета программ MAXIMA. При дифференцировании функции по нескольким переменным используется команда diff, за ней в скобках записывается функция, а дальше через запятые все переменные, по которым берутся производные, и после каждой переменной – через запятую– порядок производной. Например, мы хотим взять производную 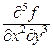, где 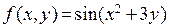. Мы вводим команду diff(sin(x^2+3*y),x,2,y,3), нажимаем клавиши Shift+Enter и получаем .

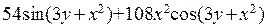Необходимое условие локального экстремума.

Теорема о необходимом условии экстремума дифференцируемой функции 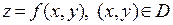. Необходимым условием существования экстремума дифференцируемой в точке 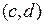функции является система равенств

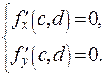
П р и м е р. Найти локальный экстремум функции 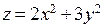, заданной на всей плоскости XOY.

Запишем необходимое условие экстремума данной функции: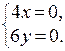

Отсюда 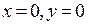. Следовательно, координаты критической точки, то есть точки, в которой частные производные первого порядка одновременно обращаются в ноль, (0,0).

Построим график функции в окрестности начала координат и проверим, действительно ли точка (0,0) является точкой локального экстремума. Введем команду plot3d(2*x^2+3*y^2,[x,-2,2],[y,-2,2]) нажмем клавиши Shift+Enter. Мы получим следующую картину.

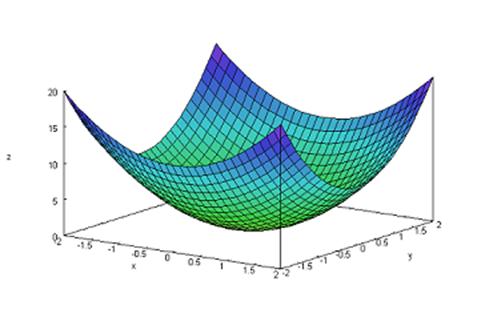
Очевидно, что в точке (0,0) локальный минимум.

Выполнение необходимого условия экстремума не обязательно обеспечивает действительное наличие экстремума в точке, то есть, критическая точка функции может не быть точкой локального экстремума. В качестве примера рассмотрим функцию двух переменных 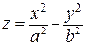. Критической точкой для этой функции является точка (0,0). Однако эта точка является не экстремальной, а седловой.

hypar.wxm

Дата добавления: 2014-01-20