
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод конечных элементов
|
|
|
|
В методе конечных элементов стержень разбивается на n элементов.

Рисунок 38. Разбиение на конечные элементы
На рисунке 38: x – глобальная координата; 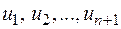 – глобальная нумерация узловых перемещений (1,2,…,n+1 – глобальная нумерация узлов).
– глобальная нумерация узловых перемещений (1,2,…,n+1 – глобальная нумерация узлов).
Рассмотрим k-й конечный элемент (рисунок 35).
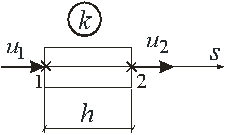
Рисунок 39. Отдельный конечный элемент
На рисунке 35: S – локальная координата; 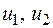 – локальная нумерация узловых перемещений (1,2 – локальная нумерация узлов).
– локальная нумерация узловых перемещений (1,2 – локальная нумерация узлов).
В пределах каждого конечного элемента функцию перемещения и нагрузки представляем в виде линейных функций:
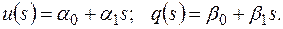 (2.6.1)
(2.6.1)
Для определения параметров 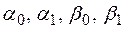 имеем следующие условия:
имеем следующие условия:
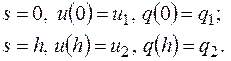 (2.6.2)
(2.6.2)
Из этих условий получаем
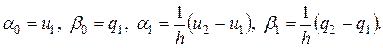 (2.6.3)
(2.6.3)
Выражения (2.6.1) с учетом (2.6.3) приобретают вид:
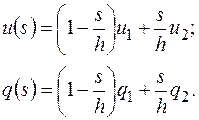 (2.6.4)
(2.6.4)
Введем обозначения
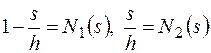 (2.6.5)
(2.6.5)
и назовем N1 и N2 функциями формы (очевидно, что N1(0)=1, N1(h)=0, N2(0)=0, N2(h)=1), тогда (2.6.4) можно записать в матричной форме
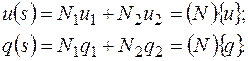 (2.6.6)
(2.6.6)
Здесь: матрица-строка функций форм
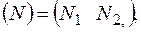 (2.6.7)
(2.6.7)
вектор узловых перемещений и вектор узловых значений нагрузки конечного элемента соответственно
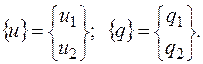 (2.6.8)
(2.6.8)
Запишем функционал энергии стержня (w - объем стержня):
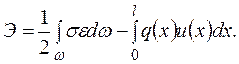 (2.6.9)
(2.6.9)
Поскольку в соответствии с законом Гука для линейной области 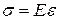 , а деформационное соотношение -
, а деформационное соотношение - 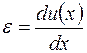 , то первый интеграл (2.6.9) приобретает вид (площадь сечения –А постоянна):
, то первый интеграл (2.6.9) приобретает вид (площадь сечения –А постоянна):
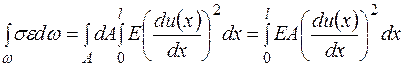 (2.6.10)
(2.6.10)
и функционал запишется так:
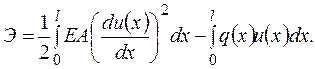 (2.6.11)
(2.6.11)
Условие минимума или стационарности функционала – равенство нулю его первой вариации:
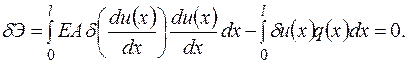 (2.6.12)
(2.6.12)
Для отдельного конечного элемента
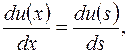 (2.6.13)
(2.6.13)
поэтому
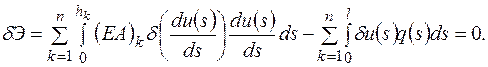 (2.6.14)
(2.6.14)
Раскроем выражения, входящие в (2.6.14) с учетом (2.6.13):
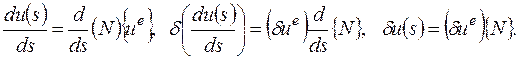 (2.6.15)
(2.6.15)
Обозначив для компактности
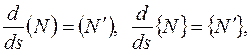 (2.6.16)
(2.6.16)
перепишем (2.6.15)
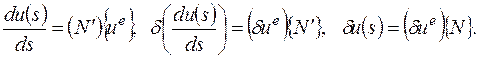 (2.6.17)
(2.6.17)
и внесем в (2.6.14)
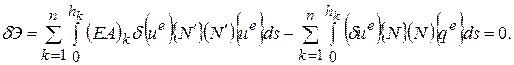 (2.6.18)
(2.6.18)
Введем обозначения:
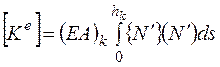 (2.6.19)
(2.6.19)
- матрица жесткости конечного элемента;
|
|
|
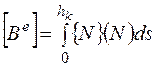 (2.6.20)
(2.6.20)
- матрица преобразования нагрузки.
С учетом введенных обозначений
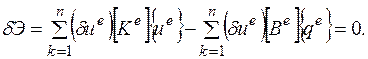 (2.6.21)
(2.6.21)
Для всей системы (стержня) после суммирования методом прямой жесткости
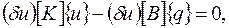 (2.6.22)
(2.6.22)
где [К] – матрица жесткости стержня;
{ u } – вектор узловых перемещений стержня.
Сокращая на вариацию вектора узловых перемещений и вводя обозначение
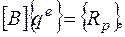 (2.6.23)
(2.6.23)
приходим к окончательной записи матричного уравнения метода конечных элементов
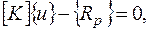 (2.6.24)
(2.6.24)
где 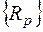 – грузовой вектор стержня.
– грузовой вектор стержня.
Вычислим значения 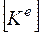 и
и 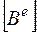 :
:
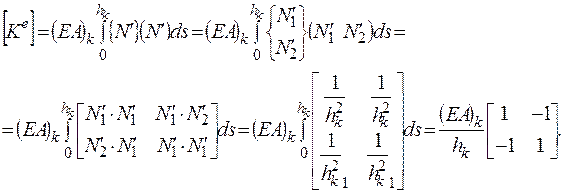 (2.6.25)
(2.6.25)
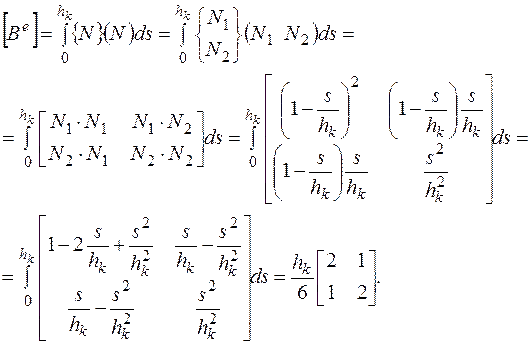 (2.6.26)
(2.6.26)
Таким образом, матрица жесткости k –го элемента
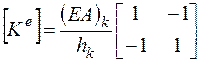 (2.6.27)
(2.6.27)
и матрица преобразования нагрузки k –го элемента
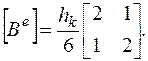 (2.6.28)
(2.6.28)
вектор внешних нагрузок -
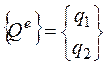 . (2.6.29)
. (2.6.29)
Матричное уравнение метода перемещений в конечноэлементной форме
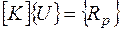 . (2.6.30)
. (2.6.30)
Здесь: матрица жесткости всей системы – [ K ], формирующаяся в соответствии с топологией системы; вектор неизвестных узловых перемещений – { U }; грузовой вектор системы -
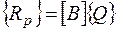 , (2.6.31)
, (2.6.31)
содержащий грузовую матрицу системы – [ B ] и вектор внешних нагрузок системы – { Q }.
Учитывая число участков (конечных элементов), запишем (2.6.30) с учетом (2.6.31) в раскрытом виде:
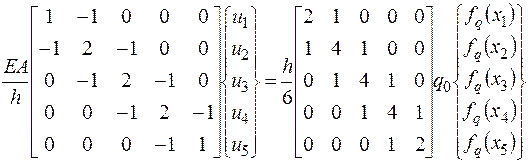 . (2.6.32)
. (2.6.32)
Умножая матрицу преобразования на вектор узловых значений нагрузки, перепишем (2.6.32):
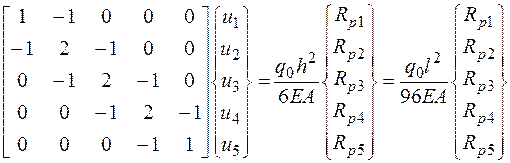 . (2.6.33)
. (2.6.33)
В методе конечных элементов учитываются только геометрические граничные условия путем обнуления строки и столбца с общим диагональным элементом – множителем при нулевом перемещении (сам диагональный элемент при этом не обнуляется) и соответствующего элемента грузового вектора. Так для варианта граничных условий А система приобретает вид:
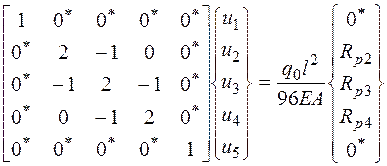 . (2.6.34)
. (2.6.34)
Для варианта граничных условий В -
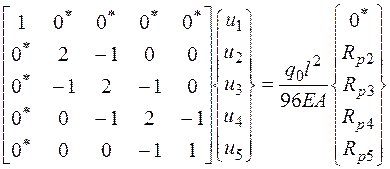 . (2.6.35)
. (2.6.35)
Для варианта граничных условий С –
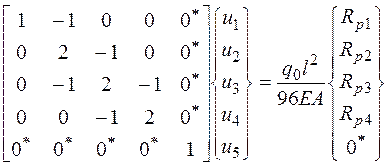 . (2.6.36)
. (2.6.36)
Решение систем уравнений производится так же, как и в методе конечных разностей. Переход к нормальным усилиям осуществляется с помощью соотношения:
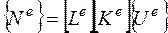 . (2.6.37)
. (2.6.37)
где 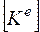 - матрица жесткости конечного элемента;
- матрица жесткости конечного элемента; 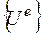 - вектор узловых перемещений конечного элемента;
- вектор узловых перемещений конечного элемента; 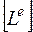 - матрица преобразования узловых реакций в продольные узловые усилия.
- матрица преобразования узловых реакций в продольные узловые усилия.
|
|
|
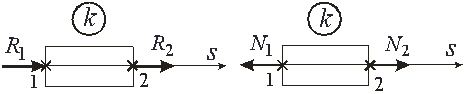
Рис. 40. Положительные направления узловых реакций (R) и узловых усилий (N) в отдельном конечном элементе
Так как направления узловых реакций конечного элемента и положительные направления внутренних сил (рис. 40) не совпадают, то матрица преобразования имеет вид:
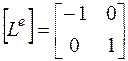 . (2.6.38)
. (2.6.38)
Произведение матрицы преобразования на матрицу жесткости конечного элемента представим в виде матрицы:
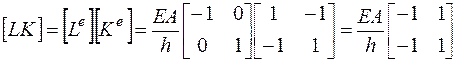 , (2.6.39)
, (2.6.39)
тогда выражение (2.6.37)примет вид:
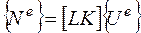 . (2.6.40)
. (2.6.40)
Для более точного определения усилий используется дифференцирующая матрица (12).
Результаты расчета представляются в виде графиков. Исходные данные вводятся в программу «GAUSS1», результаты счета по которой сравниваются с ручным счетом.
Рассмотрим пример решения варианта А.
Конечноразностное уравнение запишется так:
 (2.6.41)
(2.6.41)
После перемножения матрицы преобразования нагрузки на вектор внешних нагрузок оно примет вид:
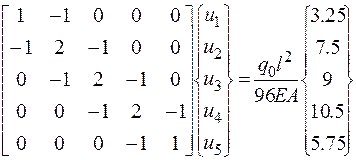 (2.6.42)
(2.6.42)
Учет геометрических граничных условий приведет к следующему соотношению:
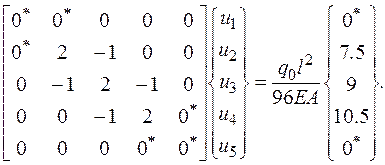 (2.6.43)
(2.6.43)
Решаем систему способом Крамера.
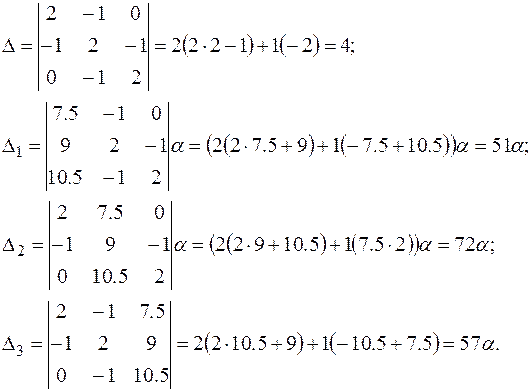 (2.6.44)
(2.6.44)
Определяем значения узловых перемещений, приводя к размерности точного решения
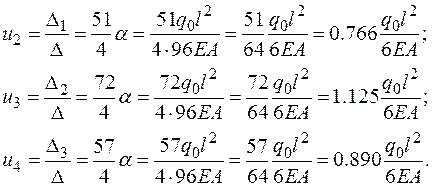 (2.6.45)
(2.6.45)
Вектор узловых перемещений, полученный в результате решения системы, имеет вид:
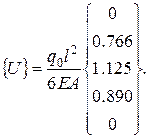 (2.6.46)
(2.6.46)
Переход от перемещений к внутренним усилиям в методе конечных элементов осуществляется с помощью матрицы жесткости элемента, то есть
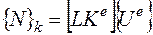 (2.6.47)
(2.6.47)
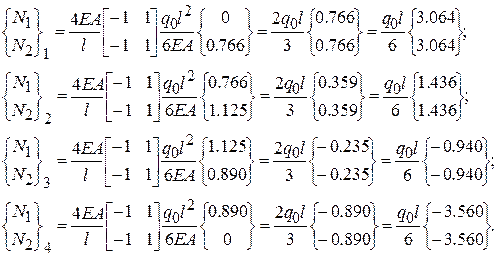 (2.6.48)
(2.6.48)
Осуществляем переход с помощью дифференцирующей матрицы.
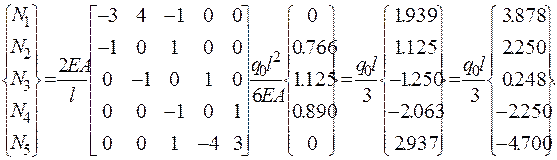 (2.6.49)
(2.6.49)
Полученные результаты представим в таблице 15 и на графиках (рис. 41, 42).
Таблица 15
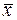
| 0.25 | 0.5 | 0.75 | 1.0 | |
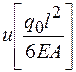
| 0* (0) | 0.766* (0.797) | 1.125* (1.125) | 0.890* (0.891) | 0* (0) |
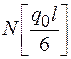
| 3.064* 3.878** (4.0) | 1.436* 2.250** (2.313) | -0.940* 0.248** (0.25) | -3.560* -2.250** (-2.188) | - -4.700** (-5) |
(…) - точное решение, * - решение в рамках МКЭ, ** - решение с помощью дифференцирующей матрицы.
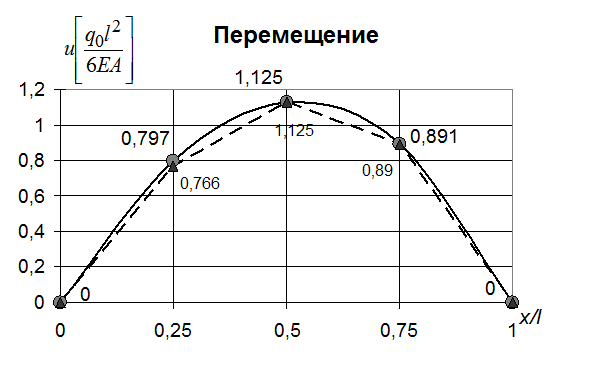
Рис. 41. Изменение продольного перемещения по длине стержня (метод конечных элементов - вариант А)
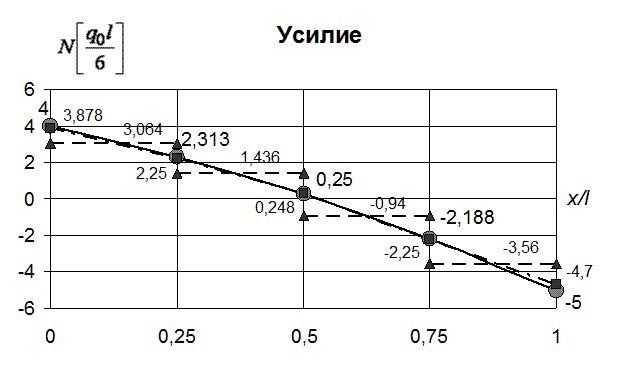
Рис. 42. Изменение продольного усилия по длине стержня (метод конечных элементов - вариант А)
Рассмотрим пример решения варианта В. Конечноразностное уравнение запишется так:
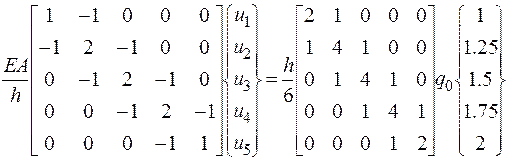 (2.6.50)
(2.6.50)
После перемножения матрицы преобразования нагрузки на вектор внешних нагрузок оно примет вид:
|
|
|
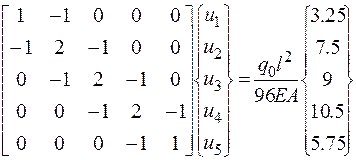 (2.6.51)
(2.6.51)
Учтем граничные условия на левом торце(u1=0)
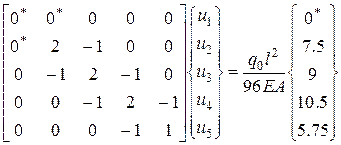 (2.6.52)
(2.6.52)
Выполним прямой ход исключения по Гауссу, идя снизу:
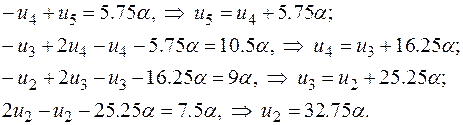 (2.6.53)
(2.6.53)
Выполним обратный ход, приводя результат к размерности точного решения
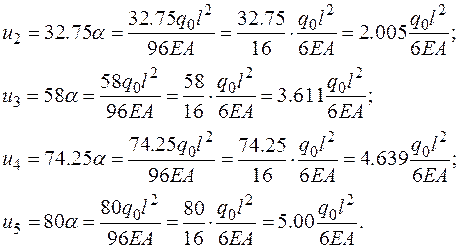 (2.6.54)
(2.6.54)
Вектор узловых перемещений, полученный в результате решения системы, имеет вид:
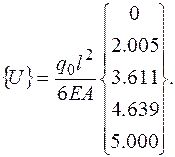 (2.6.55)
(2.6.55)
Переход от перемещений к внутренним усилиям в методе конечных элементов осуществляется с помощью матрицы жесткости элемента, то есть
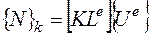 (2.6.56)
(2.6.56)
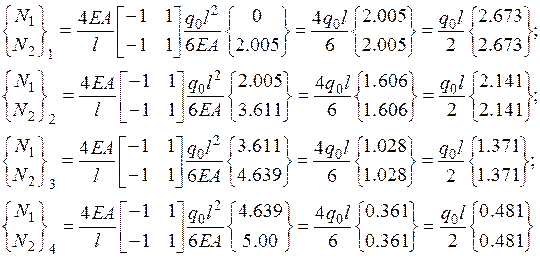 (2.6.57)
(2.6.57)
Осуществляем переход с помощью дифференцирующей матрицы.
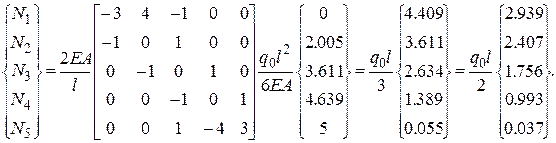 (2.6.58)
(2.6.58)
Полученные результаты представим в таблице 16 и на графиках (рис. 43, 44).
Таблица 16
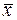
| 0.25 | 0.5 | 0.75 | 1.0 | |
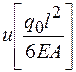
| 0* (0) | 2.005* (2.047) | 3.611* (3.625) | 4.639* (4.641) | 5.000* (5) |
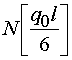
| 2.673* 2.939** (3.0) | 2.141* 2.407** (2.438) | 1.371* 1.756** (1.750) | 0.481* 0.926** (0.938) | - 0.037** (0) |
(…) - точное решение, * - решение в рамках МКЭ, ** - решение с помощью дифференцирующей матрицы.
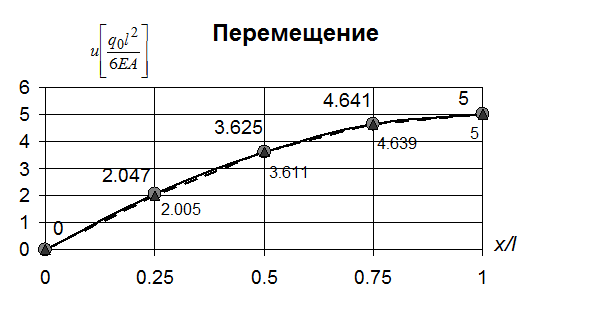
Рис 43. Изменение продольного перемещения по длине стержня (метод конечных элементов - вариант В)
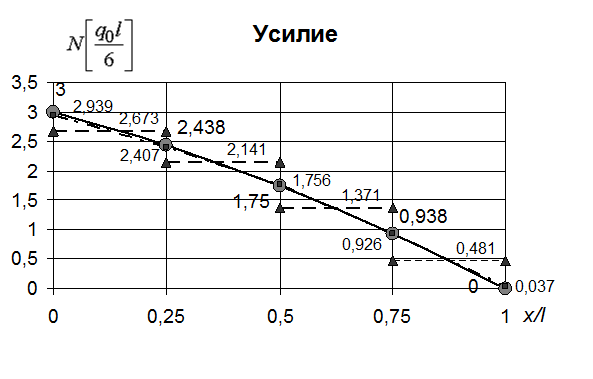
Рис. 44. Изменение продольного усилия по длине стержня (метод конечных элементов - вариант В)
Рассмотрим пример решения варианта C.
Конечноразностное уравнение запишется так:
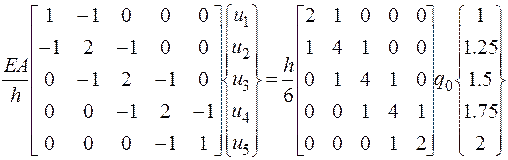 (2.6.59)
(2.6.59)
После перемножения матрицы преобразования нагрузки на вектор внешних нагрузок оно примет вид:
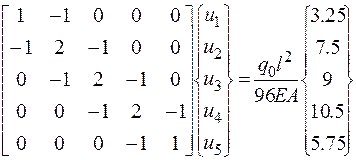 (2.6.60)
(2.6.60)
Учтем граничные условия (u5=0)
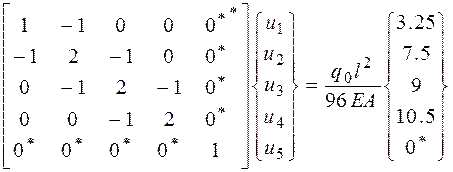 (2.6.61)
(2.6.61)
Выполним прямой ход исключения по Гауссу, идя сверху:
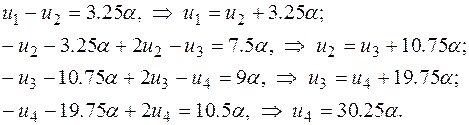 (2.6.62)
(2.6.62)
Выполним обратный ход, приводя результат к размерности точного решения
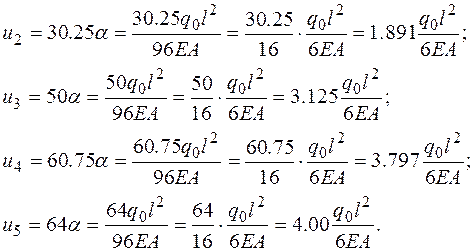 (2.6.63)
(2.6.63)
Вектор узловых перемещений, полученный в результате решения системы, имеет вид:
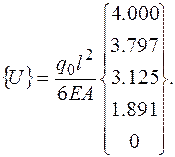 (2.6.64)
(2.6.64)
Переход от перемещений к внутренним усилиям в методе конечных элементов осуществляется с помощью матрицы жесткости элемента, то есть
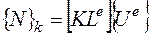 (2.6.65)
(2.6.65)
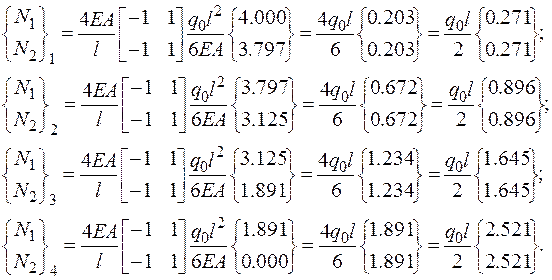 (2.6.66)
(2.6.66)
Осуществляем переход с помощью дифференцирующей матрицы.
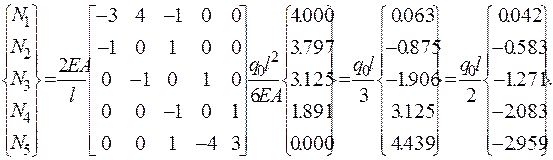 (2.6.66)
(2.6.66)
Полученные результаты представим в таблице 17 и на графиках (рис. 45, 46).
Таблица 17
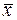
| 0.25 | 0.5 | 0.75 | 1.0 | |
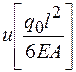
| 4* (4) | 3.797* (3.797) | 3.125* (3.125) | 1.891* (1.891) | 0* (0) |
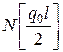
| -0.271* 0.042** (0) | -0.896* -0.583** (-0.563) | -1.645* -1.271** (-1.25) | -2.521* -2.083** (-2.063) | - -2.959** (-3) |
(…) - точное решение, * - решение в рамках МКЭ, ** - решение с помощью дифференцирующей матрицы.
|
|
|
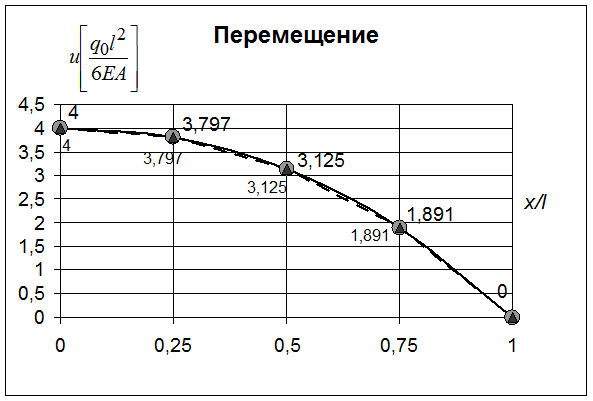
Рис 45. Изменение продольного перемещения по длине стержня (метод конечных элементов - вариант C)
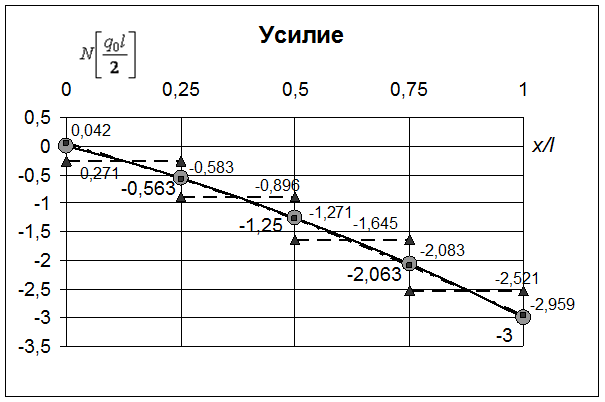
Рис. 46. Изменение продольного усилия по длине стержня (метод конечных элементов - вариант C)
В силу универсальности алгоритма в настоящее время предпочтение отдается именно методу конечных элементов.
Рекомендуемая литература
Основная литература
2. Неймарк Ю. И. Математические модели в естествознании и технике. Нижний Новгород: издание Нижегородского Университета, 2004.
3. Т. Шуп. Решение инженерных задач на ЭВМ. Перевод с английского. - М.: Мир, 1982.
4. Дж. Ортега, У. Пул. Введение в численные методы решения дифференциальных уравнений. М.: Наука, 1986.
5. В.В. Фаронов. Основы Турбо-Паскаля (в 3-х книгах). М.: МВТУ-ФЕСТО-ДИДАКТИК, 1992.
6. Р. Хершель. Турбо-Паскаль 4.0/5.0. М.: Издание МП «МИК», 1991.
7. И.А. Бабушкина, Н.А. Бушмелева, С.М. Окулов, С.Ю. Черных. Конспекты занятий по информатике (практикум по Турбо-Паскалю). Учебное пособие. К.: ВятГПУ, 1997.
Методическая литература
8. Буравлев В. Ф. Математическое моделирование в строительстве (методические указания для выполнения лабораторных работ с вариантами заданий и образцом выполнения, электронный вариант). К.: ВятГУ, 2005.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1055; Нарушение авторских прав?; Мы поможем в написании вашей работы!