Симплекс-метод

Симплекс-метод является одним из методов «целенаправленного» перебора, с постоянным приближением к решению. Для использования этого метода задачу необходимо привести к канонической форме, которая предполагает выделение базисного (опорного) решения.

КАНОНИЧЕСКАЯ ФОРМА ОЗЛП.

Канонической называется такая форма ОЗЛП, в которой

1. все свободные члены b_i ≥0;

2. для каждого из уравнений имеется переменная с коэффициентом 1 в этом уравнении и коэффициентом, равным 0, во всех остальных уравнениях;

3. целевая функция минимизируется.

Имея систему ограничений в канонической форме, можно сразу выделить допустимое решение ОЗЛП: переменные, для которых выполнено второе условие, считаются базисными и равны свободным членам. Остальные переменные будут свободными и их значение равно 0. Такое решение можно взять в качестве базисного.

ПРИМЕР 2.4.

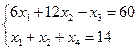
Система не приведена к канонической форме. Без преобразований выделить базисное решение нельзя.

ПРИМЕР 2.5.

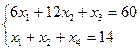
Система имеет каноническую форму. В качестве базисных можно взять переменные х₃ и х₄

Базисное решение: х₃ =60; х₄=14; х₁ =0; х₂=0

МЕТОД ЖОРДАНОВЫХ ИСКЛЮЧЕНИЙ.

Используется для поиска базисного решения, если его трудно выделить, преобразуя систему ограничений.

АЛГОРИТМ.

1. Приводим задачу к ОЗЛП.

2. Записываем условия-ограничения в виде нулевых равенств.

3. Заполняем жорданову таблицу.

Базисные переменные	Свободные члены	-x1	…	-xn
	b1	a11		a1n
	b2	a21		a2n
…
0	bm	am 1		am n

4. Выбираем разрешающий столбец – S (любой, для которого можно выполнить п.5)

5. Находим строку К, в которой достигается

6. На пересечении строки К и столбца S будет находиться генеральный элемент а_ks

7. Вычисляем

8. Строим новую жорданову таблицу 1) Х_s записываем в строку К вместо 0.

2) Столбец S вычеркиваем.

3). Элементы К строки умножаем на .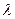

4).Все остальные элементы находим по формуле:

b_i =a_i0

9. Если в главном столбце (базисные переменные) нет нулей, то записанные в нем переменные образуют базис, в противном случае переходим к п.4

ПРИМЕЧАНИЯ.

1. Если по ходу решения задачи окажется строка, в которой все элементы отрицательные, а свободный член >0, то система не имеет неотрицательных решений

2. Если по ходу решения встретится строка, все элементы которой =0, а свободный член >0, то система решения не имеет

3. Если все переменные из главной строки перейдут в главный столбец (не останется свободных переменных), то система имеет единственное допустимое решение

4. Если столбец переменной x_j содержит одну 1, а остальные 0, то этот столбец можно вычеркнуть, заменив 0 главного столбца в строке с единицей на x_j

5. В найденном базисном решении:

а) значениями базисных переменных является столбец свободных членов;

б) свободные переменные равны нулю;

СИМПЛЕКС-МЕТОД

С помощью этого метода можно найти оптимальное решение или доказать, что задача не имеет решения.

АЛГОРИТМ:

1. Строим жорданову таблицу, включив в нее строку L.

Базисные переменные	Свободные члены	-x1	…	-xn
	b1	a11		a1n
	b2	a21		a2n
…
0	bm	am 1		am n
L	-с0	-с1		-сn

2. Находим базисное решение методом жордановых исключений

Базисные переменные	Свободные члены	-xm+1 …	-xn
x1	t10	t1m+1	t1n
x2	t20	t2m+1	t2n
…
xm	tm0	tm m+1	tm n
L	tm+1 0	tm+1 m+1	tm+1 n

3. Проверяем план на оптимальность.

План оптимален для mах: если все элементы строки L при свободных переменных ≥0,

для min: ≤0.

При выполнении условия оптимальности: значения базисных переменных равны значениям свободных членов, а значения свободных переменных равны 0.

4. Если план не оптимален, выбираем в строке L максимальный по модулю отрицательный элемент для mах, просто максимальный элемент для min. Этот столбец выбираем за разрешающий S

5. Находим строку К, в которой достигается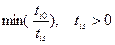

6. На пересечении строки К и столбца S будет находиться генеральный элемент t_ks

7. Вычисляем

8. Строим новую жорданову таблицу 1) Х_s и Х_k меняем местами

2) на место 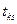. записываем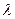

3). Элементы К строки умножаем на .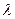

4) Элементы S столбца умножаем на – .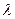

4).Все остальные элементы находим по формуле:

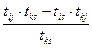
9. Переходим к п. 3.

ПРИМЕЧАНИЯ.

1. Если план оптимальный, но в строке L есть нули при свободных переменных, то задача имеет бесконечное множество оптимальных решений.
2. Если план не оптимален, но в столбце S все элементы отрицательные, т.е. нельзя найти генеральный элемент, то целевая функция неограниченна на множестве допустимых решений.

ПРИМЕР 2.4.

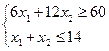
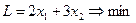
Найдем базисное решение по методу Жордановых исключений, параллельно выполняя расчеты в строке целевой функции.

1) s

базисные переменные	свободные члены	-x1	-x2	-х3	-x4
				-1
целевая функция		-2	-3

Выберем s=4, тогда по примечанию 4 метода Жордановых исключений этот столбец можно исключить.

2) s

k базисные переменные	свободные члены	-x1	-x2	-х3
				-1
x4
целевая функция		-2	-3

ПРАВИЛО. Если какое-либо уравнение системы ограничений имеет канонический вид, то из него сразу следует выделять базисную переменную.

В нашем примере: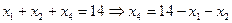

s=1; k=1 (60/6<14/1); λ=1/6

3) s

k базисные переменные	свободные члены	-x2	-х3
x1			-1/6
x4		-1	1/6
целевая функция			-1/3

Получили базисное решение. Но оно не является оптимальным. Для поиска минимума необходимо выбрать столбец x₂, т.к. коэффициент при целевой функции здесь>0

s=1; k=1; λ=1/2

4)

базисные переменные	свободные члены	-x1	-х3
x2		1/2	-1/12
x4		1/2	1/12
целевая функция		-1/2	-1/4

План оптимален, т.к. все коэффициенты при целевой функции <0

ОТВЕТ: x₁ =0; x₂ =5; х₃ =0; x₄=9; L=15

Задание. Составить математическую модель и решить графически и аналитически по вариантам.

1-5. Работник АОО «Диана» специализируется на шитье кукол 2-х видов и по договору должен выполнять за месяц работу на сумму не менее а у.е., получая за каждую куклу i -го вида р_i у.е. Спрос на куклы ограничен и равен b. Кукла i -го вида реализуется по цене с_i у.е.

Установить план заказа кукол работнику для получения максимальной прибыли при условии полной реализации кукол.

Показатели	Варианты
а
b
р1 , р2	4, 2	2, 4	1, 1	3, 1	2, 1
с1 , с2	6, 4	3, 6	6, 4	6, 3	3, 6

6-10. Абитуриенту для тестирования предложено 2 типа задач. Общее время на тестирование ограничено а минутами. Чтобы работа была засчитана, общее количество задач не должно быть меньше чем b. Время на решение одной задачи i -го типа t_i минут. Решенная задача i -го типа оценивается с_i баллами. Выбрать оптимальную стратегию абитуриента, чтобы набрать максимальное количество баллов.

Показатели	Варианты
а
b.
t1, t2	20, 10	10, 20	15, 5	5, 5	10, 15
с1 , с2	1, 1	1, 1	2, 1	10, 5	1, 2

11-15. Сухогруз может принять на борт не более а т груза, общий объём которого не должен превосходить b у.е. На причале находится груз 2 видов в неограниченном количестве. Груз i -го вида весит р_i, занимает объем v_i и стоит с_i. Выбрать вариант загрузки судна с максимальной стоимостью всего груза.

Показатели	Варианты
а
b.
р1 , р2	1, 1	3, 1	2, 1	1, 2	1, 1
v1 , v2	3, 1	1, 2	1, 3	1, 1	1, 3
с1 , с2	2, 1	1, 3	3, 1	1, 1	1, 2

16-20. АОО «Юлия» выращивает рассаду томатов 2-х видов, причем на десяток корней i -го вида затраты составляют с_i. у.е. Денежный фонд ограничен а. Максимальное количество десятков рассады, которое АОО может разместить на своем поле b.. От каждого десятка корней i -го вида рассады ожидается получить урожай р_i. кг Сколько рассады каждого вида следует вырастить, чтобы получить наибольший урожай?

Показатели	Варианты
а
b.
с1 , с2	5, 4	4, 3	1, 2	2, 1	1, 3
р1 , р2	5, 10	7, 7	10, 5	4, 5	6, 10

21-25. Для строительства требуются доски в количествене менее а куб.м. Имеются доски 2-х видов. При обработке i -го вида доски получается р_i ед. отходов. Цена доски i -го вида с_i, объем - v_i Денежный фонд ограничен b. В каком количестве следует закупить доски каждого вида, чтобы отход был минимален..

Показатели	Варианты
а
b.
с1 , с2	5, 4	1, 1	1, 3	1, 2	2, 3	3, 2
р1 , р2	1, 1	2, 1	4, 1	2, 4	2, 1	3, 2
v1 , v2	4, 3	2, 3	3, 1	2, 1	3, 1	2, 3

26-30. Детский сад собирается приобрести тарелки не менее а штук. Имеется 2 вида тарелок по цене с_i у.е. за 1 штуку i -го вида. Тарелки отличаются по сроку использования t_i Денежный фонд ограничен b. Какую следует закупить посуду, чтобы максимизировать использование тарелок.

Показатели	Варианты
а
b.
с1 , с2	20, 10	10, 5	2, 4	30, 20	10, 15	20, 10
t1 , t2	3, 2	5, 2	1, 3	2, 1	1, 2	15, 10

Дата добавления: 2014-01-20