Метод ветвей и границ. Транспортная задача в сетевой постановке

Транспортная задача в сетевой постановке.

ПОСТАНОВКА ЗАДАЧИ.

Имеется сеть (I,D,G) с заданными стоимостями перемещения единицы продукта по дуге c_d и интенсивностями вершин b_i::

b_i >0 – для пунктов отправления, i – источник;

b_i <0 – для пунктов назначения, i – сток;

b_i =0 – для нейтральных вершин.

Требуется найти оптимальный поток, для которого

При ограничениях ,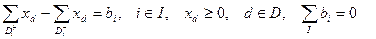

КРИТЕРИЙ ОПТИМАЛЬНОСТИ. Для того, чтобы допустимый поток был оптимальным, необходимо и достаточно существование для каждой вершины i такого числа v_i, называемого потенциалом, что для всех дуг d=(i,j)

v_j - v_i ≤ c_d, если x_d =0

v_j - v_i =c_d, если x_d >0

АЛГОРИТМ МЕТОДА ПОТЕНЦИАЛОВ.

1. Найдем допустимый невырожденный поток.

а) с помощью транспортной таблицы;

б) с помощью вспомогательной задачи:

к множеству вершин сети добавим фиктивную вершину с b₀ =0, все вершины, для которых b_i <0 соединим с нулевой вершиной входящими дугами (0,i), а для которых b_i >0 – исходящими (i,0), стоимость транспортировки для вновь добавленных дуг положим равными 1, а для остальных =0.

2. Проверим оптимальность текущего потока.

Строим систему потенциалов:

произвольно выбираем пункт i, потенциал которого полагаем равным 0;

вычисляем потенциалы вершин для которых x_d >0 по правилу

v_j = v_i +c_d, если дуга направлена от i

v_j = v_i -c_d, если дуга направлена к i

Проверяем условие оптимальности:

Если условие оптимальности выполнено, то текущий поток является оптимальным. Вычислительный процесс завершаем.

Если не выполнено, то переходим к следующему пункту.

3. Определим дугу, вводимую в поток.

Выберем ту дугу d_k, для которой достигается максимальное отклонение цены от разности потенциалов, соединяемых вершин.

4. Построим цикл.

Цикл должен содержать дугу d_k и дуги, для которых x_d >0

5. Преобразуем текущий поток.

Среди всех дуг цикла рассмотрим дуги, ориентация которых не совпадает с ориентацией дуги d_k и найдем Δ= min x_d

Преобразуем поток, добавляя Δ для всех сонаправленных с d_k дуг и отнимая Δ для всех противоположно направленных дуг.

Перейдем к пункту 2.

Метод ветвей и границ основан на упорядоченном переборе вариантов, рассмотрении лишь тех вариантов, которые оказываются по определенным признакам перспективными, и отбрасывании сразу целого множества вариантов, являющихся бесперспективными. Вначале исходное множество разбивается на некоторое число подмножеств, одно из которых включает оптимальный вариант. Для каждого из подмножеств вычисляется функция предпочтения (находится нижняя или верхняя оценка) и выбирается подмножество с оптимальной оценкой для дальнейшего ветвления. Этот процесс удобно изображать в виде дерева, вершинами которого будут рассматриваемые подмножества. Далее передвигаются с этапа на этап, выбирая каждый раз висячую вершину с оптимальным значением функции предпочтения. Полученное дерево будет деревом решения.

ПРИМЕР 3.10. Найти кратчайший путь из А в В.

М 9 К

3 2 4 3

А 3 1 2 7 В

Р 5 Т

Вначале рассмотрим 2 подмножества путей, которые являются продолжением отрезков [A, M] и [A,P]. За нижнюю оценку каждого из этих подмножеств можно взять длины дуг: v[A,M]=v[A, P]=3. Так как оценки равны, рассмотрим продолжения каждого из этих путей: v[А,М,Р]=4; v[А,М,К]=12; v[А,М,Т]=5; v[А,Р,К]=7; v[А,Р,Т]=8. Оценка нового пути до вершины Р оказалась больше предыдущей, следовательно путь [А,М,Р] отсекается. Также отсекаются пути [А,М,К] и [А,Р,Т]. Рассмотрим варианты продолжения пути с наименьшей оценкой [А,М,Т]: v[А,М,Т,В]=12. Допустимый путь получен. Однако его оценка не является наименьшей оценкой среди других висячих вершин. Рассмотрим варианты продолжения пути [А,Р,К]: v[А,Р,К,В]=10; v[А,Р,К,Т]=9. Второй вариант отбрасываем, т.к. к вершине Т существует путь с меньшей оценкой. Получили оптимальный путь [А,Р,К,В]

Метод ветвей и границ – точный метод решения задач. Он предъявляет большие требования к оперативной памяти ЭВМ. Поэтому обычно используют приближенные методы, в которых по относительно простым правилам строятся допустимые решения, которые должны быть удовлетворительными с практической точки зрения, хотя могут и не быть оптимальными.

Задача коммивояжера.

Коммивояжеру необходимо посетить N городов, заходя в каждый город 1 раз и вернуться домой. С точки зрения теории графов: найти минимальный Гамильтонов цикл.

АЛГОРИТМ ЛИТТЛА.

0. Представим граф в виде матрицы стоимостей, на главной диагонали которой стоимость = ∞.

1. Найдем в каждой строке матрицы минимальный элемент и вычтем его из всех элементов этой строки.
Если в полученной матрице оказались столбцы без нулевых элементов, то находим в каждом из них минимальный элемент и вычитаем его из всех элементов этого столбца.
Просуммируем все вычтенные элементы и получим нижнюю границу цикла в

2. Проведём оценку всех нулевых элементов матрицы.
, исключая выбранный элемент.
Выберем максимальную из оценок θ=max γ_ij=γ_kl

3. Множество путей разобьём на два подмножества: пути, содержащие дугу (k,l) и пути, не содержащие дугу (k,l).
Для второго подмножества нижней границей будет: в^/=в+ θ
Чтобы вычислить границу для первого подмножества, перейдём к матрице на порядок ниже, вычеркнув k-строку и l-столбец. В новой матрице для исключения пути (l,k) в соответствующую клетку поставим знак ∞.
Вычислим оценку полученной матрицы аналогично п.1 и добавим её к нижней границе цикла. Эта сумма в^// и будет границей для первого подмножества.

4. Сравним границы всех висячих вершин и выберем вершину с наименьшей границей. Если минимальной является граница в^/, то возвращаемся к матрице на порядок выше и, чтобы исключить дугу (k,l) из рассмотрения, заносим в соответствующую клетку знак ∞. Переходим к п.1.

5. Процесс продолжается до тех пор, пока не получим матрицу 1-ого порядка.

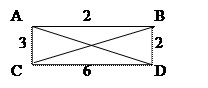
ПРИМЕР 3.11. Найти все Гамильтоновы циклы. Определить оптимальный путь коммивояжера по алгоритму Литтла.

Дата добавления: 2014-01-20