Нормирование погрешностей СИ

КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ

Процедура измерения состоит из следующих этапов: принятие модели объекта измерения, выбор метода измерения, выбор СИ, проведение эксперимента для получения результата. Это приво­дит к тому, что результат измерения отличается от истинного зна­чения измеряемой величины на некоторую величину, называемую погрешностью измерения. Измерение можно считать законченным, если определена измеряемая величина и указана возможная сте­пень ее отклонения от истинного значения.

Причины возникновения погрешностей чрезвычайно много­численны, поэтому классификация погрешностей, как и всякая другая классификация, носит достаточно условный характер.

Следует различать погрешность СИ и погрешность результата измерения этим же СИ. Погрешности измерений зависят от мет­рологических характеристик используемых СИ, совершенства вы­бранного метода измерений, внешних условий, а также от свойств объекта измерения и измеряемой величины. Погрешности изме­рений обычно превышают погрешности используемых СИ, одна­ко, используя специальные методы устранения ряда погрешно­стей и статистическую обработку данных многократных наблюде­ний, можно в некоторых случаях получить погрешность измере­ния меньше погрешности используемых СИ.

По способу выражения погрешности средств измере­ний делятся на абсолютные, относительные и приведенные.

Абсолютная погрешность — погрешность СИ, выраженная в единицах измеряемой физической величины:

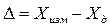
Относительная погрешность — погрешность СИ, выраженная отношением абсолютной погрешности средства измерений к ре­зультату измерений или к действительному значению измерен­ной физической величины:

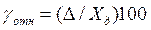
Для измерительного прибора 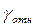характеризует погрешность в данной точке шкалы, зависит от значения измеряемой величины и имеет наименьшее значение в конце шкалы прибора.

Для характеристики точности многих средств измерений при­меняется приведенная погрешность.

Приведенная погрешность — относительная погрешность, вы­раженная отношением абсолютной погрешности СИ к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона:

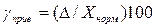
где 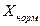— нормирующее значение, т.е. некоторое установлен­ное значение, по отношению к которому рассчитывается по­грешность.

Выбор нормирующего значения производится в соответствии с ГОСТ 8.009—84. Это может быть верхний предел измерений СИ, диапазон измерений, длина шкалы и т.д. Для многих средств измерений по приведенной погрешности устанавливают класс точ­ности прибора.

По причине и условиям возникновения погреш­ности средств измерений подразделяются на основную и допол­нительную.

Основная погрешность — это погрешность СИ, находящихся в нормальных условиях эксплуатации. Она возникает из-за неиде­альности собственных свойств СИ и показывает отличие действи­тельной функции преобразования СИ в нормальных условиях от номинальной.

Нормативными документами на СИ конкретного типа (стан­дартами, техническими условиями, калибровкой и др.) оговари­ваются нормальные условия измерений — это условия измерения, характеризуемые совокупностью значений или областей значений влияющих величин, при которых изменением результата измере­ний пренебрегают вследствие малости. Среди таких влияющих ве­личин наиболее общими являются температура и влажность окру­жающей среды, напряжение, частота и форма кривой питающего напряжения, наличие внешних электрических и магнитных полей и др. Для нормальных условий применения СИ нормативными документами предусматриваются:

нормальная область значений влияющей величины (диапазон зна­чений): температура окружающей среды — (20 ± 5) °С; положение прибора — горизонтальное с отклонением от горизонтального ± 2°; относительная влажность — (65±15)%; практическое отсут­ствие электрических и магнитных полей, напряжение питающей сети — (220 ±4,4) В, частота питающей сети — (50 ± 1) Гц и т.д.;

рабочая область значений влияющей величины — область значений влияющей величины, в пределах которой нормируют дополнитель­ную погрешность или изменение показаний средства измерений;

рабочие условия измерений — это условия измерений, при кото­рых значения влияющих величин находятся в пределах рабочих областей. Например, для измерительного конденсатора нормиру­ют дополнительную погрешность на отклонение температуры ок­ружающего воздуха от нормальной; для амперметра — изменение показаний, вызванное отклонением частоты переменного тока от 50 Гц (значение частоты 50 Гц в данном случае принимают за нормальное значение частоты).

Дополнительная погрешность — составляющая погрешности СИ, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной обла­сти значений. Нормируются, как правило, значения основной и дополнительной погрешностей, рассматриваемые как наибольшие для данного средства измерений.

Предел допускаемой основной погрешности — наибольшая ос­новная погрешность, при которой СИ может быть признано год­ным и допущено к применению по техническим условиям.

Предел допускаемой дополнительной погрешности — это та наи­большая дополнительная погрешность, при которой средство из­мерения может быть допущено к применению. Например, для прибора класса точности 1,0 приведенная дополнительная погреш­ность при изменении температуры на 10 °С не должна превышать ±1 %. Это означает, что при изменении температуры среды на каж­дые 10 °С добавляется дополнительная погрешность 1 %.

Пределы допускаемых основной и дополнительной погрешно­стей выражают в форме абсолютных, относительных и приведен­ных погрешностей.

Обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, определяемая пре­делами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность, назы­вается классом точности СИ. Класс точности дает возможность су­дить о том, в каких пределах находится погрешность СИ одного типа, но не является непосредственным показателем точности из­мерений, выполняемых с помощью каждого из этих средств, так как погрешность зависит также от метода измерений, условий из­мерений и т.д. Это важно учитывать при выборе СИ в зависимости от заданной точности измерений. Класс точности СИ конкретного типа устанавливают в стандартах технических требований (усло­вий) или в других нормативных документах. Например, прибор класса 0,5 может иметь основную приведенную погрешность, не превышающую 0,5 %. Вместе с тем прибор должен удовлетворять соответствующим требованиям и в отношении допускаемых допол­нительных погрешностей. Например, ГОСТ 8.401—80 устанавли­вает девять классов точности для аналоговых электромеханических приборов: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0; 6,0.

Зная класс точности СИ, можно найти максимально допустимое значение абсолютной погрешности для всех точек ди­апазона:

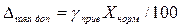
По характеру изменения погрешности средств изме­рений подразделяются на систематические, случайные и про­махи.

Систематическая погрешность — составляющая погрешности средства измерений, принимаемая за постоянную или закономер­ную изменяющуюся. Систематическая погрешность данного СИ, как правило, будет отличаться от систематической погрешности другого СИ этого же типа, вследствие чего для группы однотип­ных СИ систематическая погрешность может иногда рассматри­ваться как случайная погрешность.

К систематическим погрешностям СИ относят методические, инструментальные, субъективные и другие погрешности, которые при проведении измерений необходимо учитывать и по воз­можности устранять.

Случайная погрешность — составляющая погрешности СИ, из­меняющаяся случайным образом. Она приводит к неоднозначнос­ти показаний и обусловлена причинами, которые нельзя точно предсказать и учесть. Однако при проведении некоторого числа повторных опытов теория вероятности и математическая статис­тика позволяют уточнить результат измерения, т.е. найти значе­ние измеряемой величины, более близкое к действительному зна­чению, чем результат одного измерения.

Промахи — грубые погрешности, связанные с ошибками опе­ратора или неучтенными внешними воздействиями. Их обычно исключают из результатов измерений.

По зависимости от значения измеряемой ве­личины погрешности СИ подразделяются на аддитивные, не зависящие от значения входной величины X, и мультипликатив­ные — пропорциональные X.

Аддитивная погрешность 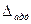не зависит от чувствительности прибора и является постоянной по величине для всех значений входной величины Х в пределах диапазона измерений (рис. 2, а). Источники данной погрешности: трение в опорах, шумы, навод­ки, вибрации. Примерами аддитивной погрешности приборов яв­ляются погрешности нуля, погрешность дискретности (квантова­ния) в цифровых приборах. От значения этой погрешности зави­сит наименьшее значение входной величины. Если прибору при­суща только аддитивная погрешность или она существенно пре­вышает другие составляющие, то предел допустимой основной погрешности нормируют в виде приведенной погрешности.

Мультипликативная погрешность зависит от чувствительности прибора и изменяется пропорционально текущему значению вход­ной величины (рис. 2, б). Источником этой погрешности явля­ются: погрешности регулировки отдельных элементов СИ (напри­мер, шунта и добавочного резистора), старение элементов, изме­нение их характеристик, влияние внешних факторов.

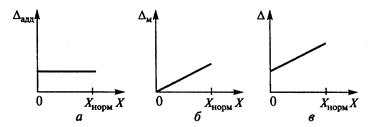
Рис. 2. Графики погрешностей измерительных приборов и преобразователей

а – аддитивной; б – мультипликативной; с - суммарной

Если прибору присуща только мультипликативная погрешность или она существенна, то предел допускаемой относительной по­грешности выражают в виде относительной погрешности. Класс точности таких СИ обозначают одним числом, помещен­ным в кружок и равным пределу допускаемой относительной по­грешности, например счетчик электрической энергии класса .

Суммарная абсолютная погрешность (рис. 2, в) определяется по формуле

,

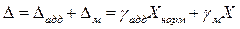где 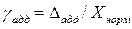— приведенное значение аддитивной погреш­ности; 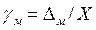— относительное значение мультипликативной погрешности.

Тогда относительная суммарная погрешность определяется по формуле

,

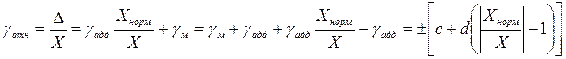где ; .

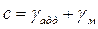Для средств измерений, у которых аддитивная и мультиплика­тивная составляющие соизмеримы, предел относительной допус­каемой основной погрешности выражается двухчленной последней форму­лой. Обозначение класса точности для них состоит из двух чисел, выражающих с и d в процентах и разделенных косой чер­той (c/d), например класс 0,02/0,01. Такое обозначение удобно, так как первый его член с равен относительной погрешности СИ в наиболее благоприятных условиях, когда 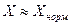. Второй член последней формулы характеризует увеличение относительной погреш­ности измерения при уменьшении X, т.е. аддитивной составля­ющей погрешности. К этой группе СИ относятся цифровые мосты, компенсаторы с ручным и автоматическим уравновешиванием.

Аддитивная и мультипликативная погрешности имеют систе­матические и случайные составляющие.

Погрешность СИ также может быть нормирована к длине шка­лы. В этом случае класс точности (1.5) обозначается одним чис­лом в процентах, помещенным между двумя линиями, располо­женными под углом, например: 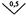. К ним относятся показыва­ющие приборы с резко неравномерной шкалой (например, ги­перболической или логарифмической). Конкретные ряды классов точности устанавливаются в стандартах на отдельные виды СИ.

В зависимости о т влияния характера изменения из­меряемой величины погрешности СИ подразделяются на статические и динамические.

Статическая погрешность — погрешность СИ, применяемого при измерении физической величины, принимаемой за неизмен­ную.

Динамическая погрешность — погрешность СИ, возникающая при измерении изменяющейся (в процессе измерений) физичес­кой величины, являющаяся следствием инерционных свойств СИ.

ЛЕКЦИЯ 3

План лекции:

1. Нормирование погрешностей СИ

Средства измерений можно использовать по назначению, если известны их метрологические свойства. Последние обычно описывают путем указания номинальных значений тех или иных характеристик и допус­каемых отклонений от них.

Эти сведения приводят в нормативно-технической документации на средства измерений, а наиболее важные из них указывают на самих средствах.

Установление номинальных значений и границ допускаемых откло­нений реальных метрологических характеристик средств измерений от их номинальных значений - нормирование метрологических характеристик.

Общим вопросам нормирования метрологических характеристик средств измерений посвящен ГОСТ 8.009-84 “Нормирование и использо­вание метрологических характеристик средств измерений”. ГОСТ устана­вливает номенклатуру метрологических характеристик средств измерений.

Для удобства использования, анализа и нормирования метроло­гических характеристик средств измерений их удобно классифици­ровать на группы, приведенные в табл. 3.

Т а б л и ц а 3

Метрологические характеристики измерительных устройств

Группа метрологических характеристик	Метрологические характеристики
Характеристики, предназначенные для определения результата измерений	Функция преобразования, коэффициент преоб­разования, цена деления, чувствительность, диа­пазон измерений, верхний и нижний пределы из­мерений, диапазон показаний, конечное и началь­ное значения шкалы
Характеристики погрешности	Систематическая погрешность, случайная по­грешность, основная погрешность, динамическая погрешность, порог чувствительности, мультипли­кативная погрешность, аддитивная погрешность, погрешности линейности, вариация, абсолютная, относительная и приведенная погрешности
Характеристики чувстви­тельности к влияющим ве­личинам	Функции влияния, дополнительная погрешность, изменение показаний, изменение коэффициента преобразований, значения неинформативного па­раметра выходного сигнала
Динамические характерис­тики	Дифференциальное уравнение, передаточная функция, комплексная частотная функция, пере­ходная характеристика, импульсная переходная характеристика, амплитудно-фазовая характерис­тика, постоянная времени, время реакции, ампли­тудно-частотная характеристика, фазочастотная характеристика, полоса пропускания и др.
Характеристики взаимо­действия с подключаемыми средствами измерения	Входной импеданс, выходной импеданс

Характеристики, предназначенные для определения результатов из­мерений (без введения поправки):

1) функция (статическая характеристика) преобразования измерительного преобразователя, а также измерительного прибора с неименованной шкалой;

2) значение однозначной или значения многозначной меры;

3) цена деления шкалы измерительного прибора или многозначной меры;

4) вид выходного кода, число разрядов кода, цена единицы наименьшего разряда кода цифровых средств измерений.

Характеристики погрешностей средств измерений:

I) характеристики систематической составляющей погрешности;

2) характеристики случайной составляющей погрешности;

3) характеристики погрешности.

Характеристики чувствительности средств измерений к влияющим величинам:

1) функции влияния;

2) изменения значений метрологических характеристик средств измерений, вызванных изменениями влияющих величин в установленных пределах. Динамические характеристики средств измерений:

1)полная;

2) частные.

Характеристики взаимодействия средств измерений с объектом исследования и нагрузкой:

1) входное полное сопротивление;

2) выходное полное сопротивление.

Неинформативные параметры выходного сигнала средств измерений.

Из указанного перечня для конкретных средств измерений выбирают такие характеристики, которые достаточны для оценки погрешностей измерений.

В настоящее время для большинства электрических средств измере­ний, используемых в статическом режиме, нормируют пределы допус­каемых погрешностей. Вопросы нормирования погрешностей для таких средств измерений рассмотрены в ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования»

Согласно этому стандарту пределы допускаемых основной и дополни­тельных погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей в зависимости от характера изменения погрешно­стей в пределах диапазона измерений, а также от условий применения и наз­начения средств измерений.

Пределы допускаемой абсолютной основной погрешности, выра­женной в единицах измеряемой величины или условно в делениях шкалы, устанавливают по формуле

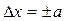
или;

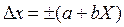
где Х - значение измеряемой величины на входе (выходе) средства измере­ний или число делений, отсчитанных по шкале;

a, b - положительные числа, не зависящие от X.

Пределы допускаемой абсолютной погрешности могут устанавли­ваться также по более сложной формуле, или в виде графика, или в виде таблицы.

Пределы допускаемой приведенной основной погрешности (в процен­тах) устанавливают по формуле

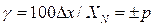
где 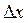- пределы допускаемой абсолютной основной погрешности

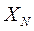- нормирующее значение - условно принятое значение измеряемой величины, выраженное в тех же единицах, что и ;

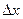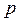- отвлеченное положительное число.

Нормирующее значение 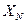для средств измерений с равномерной или степенной шкалой, а также для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, устанавливают равным большему из пределов измерений или равным большему из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений. Для электроизмерительных приборов с равномерной шкалой, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений 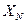допускается устанавливать равным сумме модулей пределов измерений. Практически равномерная шкала - шкала, длины делений которой разли­чаются не более чем на 30 %, а цена делений постоянна. Степенная шкала -шкала с расширяющимися или сужающимися делениями и отличная от равномерной и практически равномерной шкалы. Для средств измерений, для которых принята шкала с условным нулем (например, в градусах Цельсия), нормирующее значение устанавливают равным модулю разно­сти пределов измерений; для средств измерений с установленным номи­нальным значением нормирующее значение равно этому номинальному значению. Для измерительных приборов с существенно неравномерной шкалой (например, для омметров) нормирующее значение устанавливают равным всей длине шкалы или ее части, соответствующей диапазону изме­рений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины.

Пределы допускаемой относительной основной погрешности (в про­центах) устанавливают по формуле

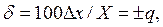
если 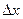установлено по формуле

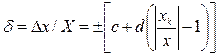
В этих выражениях q - отвлеченное положительное число;

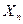- больший (по модулю) из пределов измерений;

с, d - положительные числа, причем

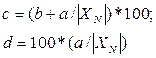
В обоснованных случаях пределы допускаемой относительной основной погрешности устанавливают по более сложной формуле, или в виде графика, или таблицы.

Значения р, q, с, d в выбирают из ряда:

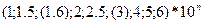, где и т.д.

Значения, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений.

Пределы допускаемых дополнительных погрешностей устанавливают в виде:

а) постоянного значения для всей рабочей области влияющей величины;

б) отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу;

в) предельной функции влияния;

г) функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния.

Предел допускаемой вариации выходного сигнала и пределы допус­каемой нестабильности выражают в виде доли допускаемой основной погрешности.

Способы выражения остальных метрологических характеристик устанавливаются в стандартах на средства измерений конкретного вида.

Классы точности средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме приведенной погреш­ности или относительной погрешности, обозначают числами, которые равны пределам, выраженным в процентах. Для средств измерений, преде­лы допускаемой основной погрешности которых принято выражать в фор­ме относительных погрешностей, классы точности обозначают числами с и. d (в процентах), разделяя их косой чертой. Для средств измерений с преде­лами допускаемой основной погрешности в форме абсолютных погрешностей классы точности обозначают буквами латинского алфавита или римскими цифрами.

Классы точности цифровых измерительных приборов со встроенны­ми вычислительными устройствами для дополнительной обработки ре­зультатов измерений устанавливают без режима обработки.

При указании классов точности на измерительных приборах с суще­ственно неравномерной шкалой допускается указывать пределы допускаемой основной относительной погрешности для части шкалы, лежащей в пределах, отмеченных специальными знаками, например точками или треугольниками.

Правила и примеры обозначения классов точности средств измерений приведены в табл. 4

Т а б л и ц а 4

Формула для предельной основной погрешности	Пределы допускаемой основной погрешности %	Обозначение класса точности на средства измерений
в общем виде	пример
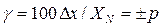
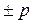
		p или	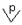1.5 или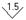
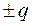
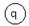
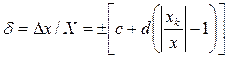
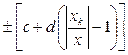
		c/d	0.02/0.01
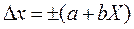
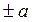
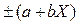
		Римскими цифрами или латинскими буквами	L

ЛЕКЦИЯ 4

План лекции:

1. Структурные схемы приборов прямого и уравновешивающего преобразования.

2. Государственная система промышленных приборов и средств автоматизации

3. Цифровые измерительные приборы

4. Виртуальные информационно-измерительные приборы

4.1 основные понятия

4.2 средства измерения и тестирования

4.3 программное обеспечение

Дата добавления: 2014-01-20