
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие замечания по поводу методов Ритца, Бубнова –Галёркина и других прямых методов
|
|
|
|
Средствами функционального анализа доказано, что в конечномерном подпространстве гильбертова пространства (а - гильбертово пространство) всегда есть элемент наилучшего приближения.
Содержание темы
Входная информация для самопроверки
ММ-6. Ключевые слова и понятия
МЕТОДЫ РИТЦА И БУБНОВА-ГАЛЁРКИНА
ММ-6. ДИСКРЕТИЗАЦИЯ ФУНКЦИОНАЛЬНОГО ПРОСТРАНСТВА.
6.1. Элемент наилучшего приближения
6.2. Координатная функция
6.3. Координатная система
6.4. Метод Ритца
6.5. Метод Бубнова-Галёркина
Для изучения данной темы Вам необходимо восстановить в памяти:
- из курса прикладной математики - понятия линейной алгебры, векторной алгебры, числовой последовательности, функциональной последовательности, предела;
- из настоящего спецкурса - понятия: пространства, оператора, функционала, линейного оператора, проекции, системы функций, базиса, ортогональной системы функций, полной системы.
 6.2.1. Структурно – логическая схема содержания темы
6.2.1. Структурно – логическая схема содержания темы

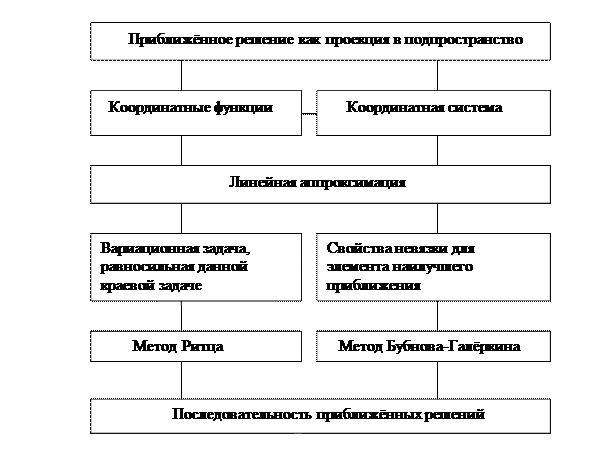
 6.2.2. Тематическое содержание
6.2.2. Тематическое содержание
В лекции ММ-1 мы выяснили, что одной из проблем, возникающих при расчёте строительных конструкций, является то, что они моделируются системами с бесконечно большим числом степеней свободы, в то время, как в памяти компьютера или даже на листе бумаги можно записать только конечное количество чисел. Таким образом возникает задача, упомянутая в лекции ММ-1 – дискретизация рассчитываемой системы и аппроксимация искомой функции (искомых функций) элементами подходящего для данного случая дискретного множества. Это позволяет преодолеть поставленную проблему, так как каждый элемент дискретного множества может быть задан конечным числом чисел. Об искомых функциях известно только то, что они являются решением некоторой краевой задачи для обыкновенного дифференциального уравнения или дифференциального уравнения в частных производных, либо для систем таких уравнений; в общем случае можно сказать, что они удовлетворяют некоторому операторному уравнению, то-есть, они заданы неявно – операторным уравнением. В курсе информатики и вычислительной техники рассматривалась значительно более простая задача – аппроксимация функций, заданных явно (например, эмпирических зависимостей, заданных таблицей).
|
|
|
Известны два пути построения методов такой аппроксимации.
Первый из этих путей предусматривает дискретизацию континуальной области путём приближённого её представления некоторым конечным множеством её точек. Это множество называется сеткой узлов, а соответствующие методы называются сеточными методами, или методами конечных разностей (МКР). Учитывая, что эти методы сейчас в значительной степени потеряли актуальность для строительной механики, а также изобилие посвящённой им литературы, в данном спецкурсе они не рассматриваются.
Второй путь – дискретизация пространств искомых и заданных (описывающих нагрузки и воздействия) функций. В этой связи обычно упоминают пересекающиеся классы методов – прямые методы, вариационные методы, энергетические методы, проекционные методы, методы наименьших квадратов, методы Ритца, типа Бубнова-Галёркина и некоторые другие.
Возможна также комбинация этих путей, реализованная в методе конечных элементов (МКЭ).
Двумя последними направлениями мы и займёмся далее.
Второй путь чаще всего использует линейную аппроксимацию функций – её приближённое представление линейной комбинацией функций некоторой заранее выбранной системы 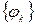 . Тогда приближённое решение задачи заключается в определении коэффициентов этой комбинации. Для этого применяется ряд методов (методы Ритца, Бубнова – Галёркина и его обобщения, наименьших квадратов, колллокаций, Бицено-Коха и ряд других методов). В различных условиях может оказаться рациональным применение различных методов или даже невозможным применение каких-то методов. Границы областей рационального применения этих методов не всегда чётко очерчены. Далее мы остановимся на двух наиболее распространённых методах – Ритца и Бубнова–Галёркина.
. Тогда приближённое решение задачи заключается в определении коэффициентов этой комбинации. Для этого применяется ряд методов (методы Ритца, Бубнова – Галёркина и его обобщения, наименьших квадратов, колллокаций, Бицено-Коха и ряд других методов). В различных условиях может оказаться рациональным применение различных методов или даже невозможным применение каких-то методов. Границы областей рационального применения этих методов не всегда чётко очерчены. Далее мы остановимся на двух наиболее распространённых методах – Ритца и Бубнова–Галёркина.
|
|
|
Линейная аппроксимация функций напоминает задание вектора при помощи чисел. С этой целью в трёхмерном пространтве векторной алгебры вводится система координат - совокупность осей координат, пересекающихся в одной точке. На этих осях задаются координатные орты, фиксирующие направление и масштаб. Совокупность координатных функций образует базис. Проектируя вектор на ось, получаем также вектор - компоненту (или составляющую) заданного вектора, длина которой называется координатой вектора. Используется также термин проекция вектора, под которой в ряде учебников (в основном для технических учебных заведений) подразумевается число – координата вектора; в более серьёзной специальной литературе под координатой вектора подразумевается другой вектор - его компонента вдоль данной оси.
Для наших целей более удобно называть проекцией вектора другой вектор – составляющую, или компоненту заданного вектора. На элементарном уровне это можно пояснить следующим образом. Часто кроме проекции вектора на ось (одномерное подпространство трёхмерного пространства) необходимо использовать также результат его проектирования на плоскость (двумерное подпространство трёхмерного пространства), который в принципе невозможно задать одним числом и который естественно рассматривать как вектор. Этот вектор естественно называть проекцией заданного вектора на плоскость; тогда и проекцию вектора на ось так же естественно считать вектором.
В общем случае, как установлено в векторной алгебре, в конкретной системе координат любой вектор 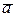 может быть представлен при помощи других векторов (координатных ортов) в виде
может быть представлен при помощи других векторов (координатных ортов) в виде
 , (6.1)
, (6.1)
где  ,
, 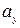 ,
,  - координаты этого вектора;
- координаты этого вектора; 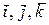 - орты координатной системы.
- орты координатной системы.
Так как рассматриваемое пространство трёхмерно, необходимое и достаточное количество координат для точного задания вектора - три, а указанная система ортов полна в этом пространстве. Кроме того, приведенная выше система ортов линейно независима, то-есть, не существует такой тройки чисел 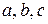 , для которой линейная комбинация
, для которой линейная комбинация  задавала бы ненулевой вектор.
задавала бы ненулевой вектор.
|
|
|
Ось и плоскость являются подпространствами меньшей размерности трёхмерного пространства векторной алгебры (ось – одномерное подпространство, плоскость – двумерное). Иногда, для конкретных условий той или иной задачи, достаточно вместо самого вектора указывать только его проекцию на подпространства – плоскость или даже ось. Так, для многих целей достаточно рассматривать вместо траектории самолёта его след на карте (считаем расстояния достаточно малыми, чтобы пренебречь кривизной земной поверхности) или даже его расстояние до пункта назначения – длину его проекции на ось, проходящую через пункт вылета и пункт назначения. При этом мы пренебрегаем либо одной проекцией (проекцией на вертикаль) либо двумя проекциями (на вертикаль и на одну перпендикулярную к ней ось, лежащую в плоскости карты). Следовательно, мы пользуемся упрощенным, приближённым представлением вектора – его проекцией на подпространство меньшей размерности:
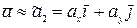 , (6.2)
, (6.2)
 . (6.3)
. (6.3)
Здесь индекс  приближённого представления
приближённого представления  равен размерности подпространства, в котором лежит аппроксимирующий вектор.
равен размерности подпространства, в котором лежит аппроксимирующий вектор.
Важно, чтобы отброшенная составляющая вектора, перпендикулярная к его приближённому представлению, была достаточно малой, то-есть, чтобы отброшенные проекции 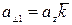 ,
,  ;
; 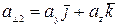 ,
, 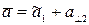 имели достаточно малую норму
имели достаточно малую норму 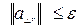 (
(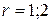 ), где
), где 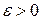 - достаточно малая величина. Очевидно,что погрешность проекции на подпространство большей размерности (плоскость, а не ось) меньше или равна погрешности проекции на подпространство меньшей размерности то-есть, (ось). Это следует из свойства треугольника
- достаточно малая величина. Очевидно,что погрешность проекции на подпространство большей размерности (плоскость, а не ось) меньше или равна погрешности проекции на подпространство меньшей размерности то-есть, (ось). Это следует из свойства треугольника  .
.
Обобщим это положение на произвольное гильбертово пространство (для нас важен его частный случай – функциональное пространство  ) или на его полное подпространство любой (конечной или бесконечной) размерности. По аналогии с введением системы координатных ортов в трёхмерном пространстве зададим в нём базис - систему функций
) или на его полное подпространство любой (конечной или бесконечной) размерности. По аналогии с введением системы координатных ортов в трёхмерном пространстве зададим в нём базис - систему функций  (если пространство конечномерно) или
(если пространство конечномерно) или  (если пространство бесконечномерно), которые назовём координатными функциями. Они будут играть роль координатных ортов. Естественно, по причинам, упомянутым в лекции ММ-1, для конкретных вычислительных процессов можно применять только конечные системы функций; бесконечные системы необходимы для теоретического анализа того или иного метода. Как в случае вектора в трёхмерном пространстве векторной алгебры, мы будем пытаться представить искомую или заданную функцию
(если пространство бесконечномерно), которые назовём координатными функциями. Они будут играть роль координатных ортов. Естественно, по причинам, упомянутым в лекции ММ-1, для конкретных вычислительных процессов можно применять только конечные системы функций; бесконечные системы необходимы для теоретического анализа того или иного метода. Как в случае вектора в трёхмерном пространстве векторной алгебры, мы будем пытаться представить искомую или заданную функцию 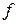 (в случае системы уравнений – искомые или заданые функции) в виде линейной комбинации
(в случае системы уравнений – искомые или заданые функции) в виде линейной комбинации
|
|
|
в случае конечномерного пространства -
 , (6.4)
, (6.4)
в случае бесконечномерного пространства –
 . (6.5)
. (6.5)
Как правило, искомые функции принадлежат бесконечномерным пространстам и в лучшем случае точно могут быть представлены только бесконечной линейной комбинацией (6.5), понимаемой по аналогии с суммой ряда (в случае, если пространство сепарабельно, как, например, пространство  ). В общем случае конечные системы являются неполными в функциональных пространствах, в которых мы разыскиваем решение. Другими словами, входящих в них функций недостаточно для точного описания решения. и они служат для приближённого описания решения (иными словами, для его аппроксимации) – его проектирования на подпространства
). В общем случае конечные системы являются неполными в функциональных пространствах, в которых мы разыскиваем решение. Другими словами, входящих в них функций недостаточно для точного описания решения. и они служат для приближённого описания решения (иными словами, для его аппроксимации) – его проектирования на подпространства  , натянутые на
, натянутые на  (это означает - на линейные оболочки этой системы – множества функций, которые можно записаь в виде (6.4) точно).
(это означает - на линейные оболочки этой системы – множества функций, которые можно записаь в виде (6.4) точно).
Разложения (6.4) и их коэффициенты принято для удобства анализа снабжать верхними индексами (в скобках), равными количеству координатных функций, используемых в данном решении, то-есть, размерности подпространства приближённых решений, обозначение которого будем также снабжать этим верхним индексом.
Таким образом, точные решения должны аппроксимироваться конечными суммами вида (6.4) (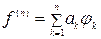 ). При этом в случае правильного применения метода приближённое решение, отмеченное звёздочкой,
). При этом в случае правильного применения метода приближённое решение, отмеченное звёздочкой, 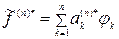 , является элементом наилучшего приближения, то-есть, таким элементом, что норма его погрешности будет наименьшей на
, является элементом наилучшего приближения, то-есть, таким элементом, что норма его погрешности будет наименьшей на 
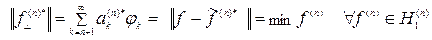 :
:
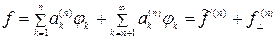 . (6.6)
. (6.6)

Однако, погрешность такой аппроксимации не может быть установлена априори, а приведенные в литературе её оценки практически нереализуемы в процессе расчёта и максимум, на что можно надеяться, так это на возможность сравнения оценок для различных вариантов метода или различных методов.
Поэтому грамотное применение описываемых методов состоит в том, что выполняется последовательность расчётов с увеличивающимся количеством координатных функций. В каждом из таких расчётов осуществляется проектирование искомой функции (искомых функций) в подпространства всё большей размерности. В результате мы получаем последовательность приближённых решений. По аналогии со случаем (6.1) – (6.3) мы можем сказать, что вполне возможна такая ситуация, когда каждое следующее решение будет точнее предыдущего. Однако, в общем случае необходим более строгий анализ условий, при выполнении которых:
а) последовательность таких приближённых решений имеет предел при 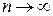 и б) этот предел равен точному решению.
и б) этот предел равен точному решению.
На языке формул такое предположение выглядит так:
 , (6.7)
, (6.7)
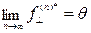 , (6.8)
, (6.8)
где 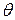 - нулевой элемент (.
- нулевой элемент (.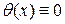 ).
).
Указанные выше условия исходят из фундаментальных свойств дифференциальных операторов строительной механики в задачах, сформулированных в пространстве перемещений (метод перемещений) или в пространстве усилий (метод сил).
Рассмотрим этот вопрос подробнее на примере задачи, сформулированной в перемещениях. Пусть рассматриваются для простоты изложения перемещения  и нагрузка
и нагрузка  одного направления. Тогда линейная краевая задача для дифференциального уравнения
одного направления. Тогда линейная краевая задача для дифференциального уравнения 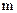 -го порядка строительной механики имеет вид
-го порядка строительной механики имеет вид
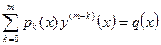 , (6.9)
, (6.9)
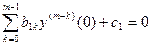 , (6.10)
, (6.10)
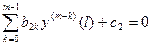 , (6.11)
, (6.11)
где  -коэффициенты.
-коэффициенты.
Если  , краевые условия называются однородными, в противном случае – неоднородными.
, краевые условия называются однородными, в противном случае – неоднородными.
Введя операторы  и
и 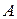 - совокупность оператора
- совокупность оператора 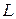 и краевых условий (6.10), (6.11), запишем задачу (6.9) – (6.11) в виде
и краевых условий (6.10), (6.11), запишем задачу (6.9) – (6.11) в виде
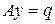 . (6.12)
. (6.12)
Как следует из смысла метода перемещений, левая часть уравнения (6.9), то-есть,  , есть равнодействующая внутренних сил. Тогда, как установлено в курсе строительной механики, работа внутренних сил первого состояния (описываемого возможными перемещениями
, есть равнодействующая внутренних сил. Тогда, как установлено в курсе строительной механики, работа внутренних сил первого состояния (описываемого возможными перемещениями  ), на перемещениях второго состояния (описываемого возможными перемещениями
), на перемещениях второго состояния (описываемого возможными перемещениями 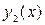 ), равна (здесь скалярное произведение определяется согласноформулы (2.12) лекции ММ-2)
), равна (здесь скалярное произведение определяется согласноформулы (2.12) лекции ММ-2)
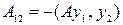 . (6.13)
. (6.13)
Теорема о взаимности работ для состояний, описываемых возможными перемещениями  и
и 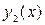 , при однородных краевых условиях позволяет записать
, при однородных краевых условиях позволяет записать
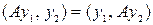 . (6.14)
. (6.14)
Операторы 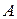 , удовлетворяющие условию (6.14), называются симметричными, если
, удовлетворяющие условию (6.14), называются симметричными, если 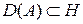 ; если же
; если же  , то такие симметричные операторы называется самосопряжёнными. Если для самосопряжённого оператора
, то такие симметричные операторы называется самосопряжёнными. Если для самосопряжённого оператора 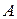 можно указать такую величину
можно указать такую величину  , не зависящую от функции, на которую действует оператор, что выполняется неравенство
, не зависящую от функции, на которую действует оператор, что выполняется неравенство
 , (6.15)
, (6.15)
то такой оператор называется положительно определённым.
Операторы, с которыми мы будем иметь дело, - положительно определённые. Механический смысл этого неравенства – действительная потенциальная энергия внутренних сил всегда положительна и её отношение к ненулевой норме нагрузки не может стать как угодно малым. Следует, однако, отметить, что все положения настоящей лекции могут быть распространены на более общий случай только положительных операторов (удовлетворяющих условию 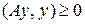 ), если у рассматриваемой краевой задачи имеется только единственное решение.
), если у рассматриваемой краевой задачи имеется только единственное решение.
Теперь мы можем перейти к условиям, которым должны удовлетворять координатные функции и их система в целом (напоминаем, что эти условия зависят от того, какой метод аппроксимации мы применяем).
Вначале рассмотрим случай, когда краевые условия (6.10) и (6.11) однородны.
Таких условий четыре. Три из них обеспечивают возможность реализации рассматриваемых методов в идеализированной ситуации, когда числа могут иметь сколь угодно большую длину и их округление не нужно. При вычислениях с округлением чисел эти три условия также должны выполняться, но возникает проблема неустойчивости счёта из-за потери точности, связанной с округлением. Эта проблема преодолевается, если выполняется четвёртое условие.
Условие 1. Для метода Ритца  , для метода Бубнова-Галёркина
, для метода Бубнова-Галёркина 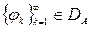 , где
, где  - энергетическое пространство оператора
- энергетическое пространство оператора 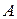 ,
, 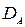 - его область определения.
- его область определения.
Смысл требования для метода Бубнова-Галёркина очевиден: чтобы функция принадлежала области определения оператора краевой задачи, необходима и достаточна возможность
а) взять все производные дифференциального оператора,
б) удовлетворить краевым условиям (однородным).
Итак, координатные функции в методе Бубнова-Галёркина должны быть  раз дифференцируемыми и удовлетворять заданным однородным граничным условиям.
раз дифференцируемыми и удовлетворять заданным однородным граничным условиям.
Очевидно, сходимость последовательности приближёных решений этого метода может контролироваться обычной нормой разности (2.5), (2.12), (2.13) лекции ММ-2.
В случае метода Ритца должна использоваться энергетическая норма, описанная в лекции ММ-3. Следовательно, должны браться интегралы при определении энергетического скалярного произведения и, в частности, энергетического скалярного квадрата функции


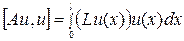 . (6.16)
. (6.16)
Кроме того, энергетическое пространство оператора отличается от его области определения наличием пределов всех последовательностей функций из его области определения. (сходимость к этим пределам теперь определяется энергетической нориой). Учёт краевых условий практически аналогичен их учёту в методе Бубнова-Галёркина.
Требование дифференцируемости  раз при однородных краевых условиях может быть ослаблено (вплоть до дифференцируемости
раз при однородных краевых условиях может быть ослаблено (вплоть до дифференцируемости 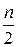 раз) благодаря возможности понижения порядка производной в (6.16) при выполнениии интегрирования по частям (возможно – неоднократного), например,
раз) благодаря возможности понижения порядка производной в (6.16) при выполнениии интегрирования по частям (возможно – неоднократного), например,



=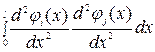 ; (6.17)
; (6.17)
здесь учтено, что однородные краевые условия обнуляют внеинтегральные члены.
При  учёт всех краевых условий затруднителен. В связи с этим используется факт, установленный в вариационном исчислении – математической дисциплине, объектом которой являются методы отыскания функций, сообщающих заданному функционалу минимальное значение (как мы выясним позднее, изучаемые нами методы сводят решение краевой задачи к задаче вариационной). Этот факт заключается в том, что среди краевых условий имеются такие, которые необходимо точно учитывать при выборе координатных функций (они называются главными) и такие, которые приближённо удовлетворяются автоматически при решении задачи (естественные краевые условия). Учёт естественных краевых условий при выборе координатных функций не обязателен.
учёт всех краевых условий затруднителен. В связи с этим используется факт, установленный в вариационном исчислении – математической дисциплине, объектом которой являются методы отыскания функций, сообщающих заданному функционалу минимальное значение (как мы выясним позднее, изучаемые нами методы сводят решение краевой задачи к задаче вариационной). Этот факт заключается в том, что среди краевых условий имеются такие, которые необходимо точно учитывать при выборе координатных функций (они называются главными) и такие, которые приближённо удовлетворяются автоматически при решении задачи (естественные краевые условия). Учёт естественных краевых условий при выборе координатных функций не обязателен.
При решении задач строительной механики в перемещениях (метод перемещений) главные, обязательно учитываемые условия – кинематические, или геометрические (перемещения и углы поворота краевых сечений). Статические (динамические) условия – естественные.
Если статические условия неоднородны, их иногда удобно включать в нагрузку.
В общем случае неоднородные краевые условия могут учитываться следующим образом. Линейная аппроксимация записывается в виде
 , (6.18)
, (6.18)
где  - любая функция, удовлетворяющая неоднородным краевым условиям (6.10) и (6.11) и условию
- любая функция, удовлетворяющая неоднородным краевым условиям (6.10) и (6.11) и условию  (то-есть, требуется наличие производных порядка до
(то-есть, требуется наличие производных порядка до  включительно).При этом функции
включительно).При этом функции 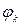 при
при 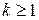 должны удовлетворять соответствующим однородным условиям (при
должны удовлетворять соответствующим однородным условиям (при  ) и условию
) и условию  . Подставим линейную комбинацию (6.18) в уравнение (6.9). Вследствие линейности оператора
. Подставим линейную комбинацию (6.18) в уравнение (6.9). Вследствие линейности оператора 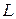 это приведёт к уравнению
это приведёт к уравнению
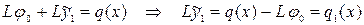 , (6.19)
, (6.19)
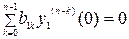 , (6.20)
, (6.20)
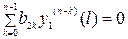 , (6.21)
, (6.21)
то-есть, мы получили задачу, аналогичную (6.9)-(6.11), но с исправленной правой частью, однородными краевыми условиями и новой неизвестной функцией.
Учитывая изложенное, далее рассматриваем только случай однородных граничных условий.
Следует отметить большую роль ортонормированных координатных систем  , удовлетворяющих условиям
, удовлетворяющих условиям  при
при 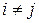 и
и  при
при 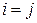 . Такая система полна в
. Такая система полна в 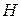 , если в
, если в 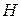 нет элементов, которые ей не принадлежат, но ортогональны ко всем её элементам.
нет элементов, которые ей не принадлежат, но ортогональны ко всем её элементам.
Роль таких систем обусловлена тем, что любой элемент 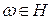 , ортогональный всем элементам полной в
, ортогональный всем элементам полной в 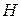 ортонормированной системы, является нулевым элементом.
ортонормированной системы, является нулевым элементом.
Если для любой функции 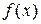 вычислять числа
вычислять числа  при возрастающих
при возрастающих  , то линейная комбинация
, то линейная комбинация  , называемая частичной суммой ряда Фурье функции
, называемая частичной суммой ряда Фурье функции 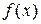 по отношению к системе
по отношению к системе  , стремится к
, стремится к 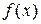
 , (6.22)
, (6.22)
и, следовательно, остаток ряда
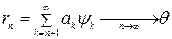 . (6.23)
. (6.23)
В нашем случае 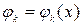 или
или  .
.
Условие 2. Функции координатной системы должны быть линейно независимыми.
Условие 3. Координатная система должна быть полной в 
Понятия линейной независимости и полноты системы функций разъяснены в лекции ММ-3.
Условие 4. В идеальном случае вычислений без округлений (с числами, записываемыми бесконечным количеством цифр) указанных трёх условий достаточно, чтобы система удовлетворяющих им координатных функций позволяла осуществить расчёт либо методом Ритца, либо методом Бубнова-Галёркина. Однако, в реальных условиях, при выполнении вычислений с округлением, погрешности могут сделать расчёт невозможным. Чтобы избежать подобной ситуации, неодходимо, чтобы собственные числа введенной ниже формулой (6.28) матрицы Ритца были ограничены снизу и сверху постоянными, не зависящими от количества принятых координатных функций.
Итак, роль элементов базиса 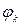 в
в 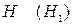 аналогична роли координатных ортов в трёхмерном пространстве векторной алгебры. Эти элементы называются координатными элементами, или, в случае функциональных пространств
аналогична роли координатных ортов в трёхмерном пространстве векторной алгебры. Эти элементы называются координатными элементами, или, в случае функциональных пространств 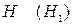 (и, прежде всего, пространства
(и, прежде всего, пространства  ) координатными функциями.
) координатными функциями.
|

Теперь мы можем перейти к методам аппроксимации – то-есть, к методам определения коэффициентов  , которые аналогичны координатам вектора (в косоугольной системе кооринат, если координатная система неортогональна, и в прямоугольной системе координат – если эта система ортогональна).
, которые аналогичны координатам вектора (в косоугольной системе кооринат, если координатная система неортогональна, и в прямоугольной системе координат – если эта система ортогональна).
Метод Ритца. В основе этого метода лежит устанавливаемый в функциональном анализе факт: решение краевой задачи (6.9) - (6.11), операторное представление которой имеет вид
 (6.24)
(6.24)
с положительно определённым оператором 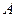 , можно поставить в соответствие задачу поиска такой функции
, можно поставить в соответствие задачу поиска такой функции 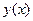 , которая сообщает минимум функционалу
, которая сообщает минимум функционалу
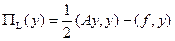 . (6.25)
. (6.25)
И, наоборот, каждой задаче поиска минимума этого функционала соответствует краевая задача указанного вида. Это соответствие означает, что, если некоторая функция является решением задачи (6.9) - (6.11), то она, будучи подставлена в выражение (6.24), одновременно сообщает минимум функционалу (6.25), а если она сообщает минимум функционалу (6.25), то она одновременно является решением краевой задачи (6.9) - (6.11).
Заметим, что выражение (6.25) в задачах строительной механики линейно упругих систем имеет чёткий физический смысл. Так, в упрощенном случае, (например, прогиб в случае чистого изгиба) первое слагаемое
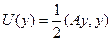 (6.26)
(6.26)
явлется половиной скалярного произведения обобщённой внутренней силы, действующей на элемент конструкции, на перемещение этого элемента, то - есть. действительной работой внутренних сил, взятой с обратным знаком, или потенциальной энергией деформирования.
Аналогично этому в указанном случае
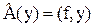 (6.27)
(6.27)
равно действительной работе внешних сил, то - есть, 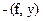 равно изменению потенциальной энергии внешних сил.
равно изменению потенциальной энергии внешних сил.
В общем случае указанный физический смысл сохраняется, однако, 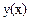 уже является не функцией, а вектор-функцией, координаты которой имеют смысл обобщенных перемещений элемента конструкции; при этом
уже является не функцией, а вектор-функцией, координаты которой имеют смысл обобщенных перемещений элемента конструкции; при этом  является вектор - функцией внутренних усилий.
является вектор - функцией внутренних усилий.
Выражение (6.25) является, таким образом, изменением полной потенциальной энергии системы. Иногда его называют функционалом Лагранжа. Вне зависимости от физического смысла задачи, если её оператор обладает указанными в настоящей лекции свойствами, этот функционал называют функционалом энергии.
Задачи поиска экстремума функционала 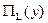 (то-есть, поиска такой функции
(то-есть, поиска такой функции 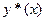 , что
, что  ) тоже в подавляющем большинстве случаев не могут быть решены в замкнутом виде, поэтому они решаются численно.
) тоже в подавляющем большинстве случаев не могут быть решены в замкнутом виде, поэтому они решаются численно.
Обычно решение этой задачи сводится к поиску такой последовательности приближённых решений  , что
, что  ,
,  . Такая последовательность называется минимизирующей для функционала (6.25).
. Такая последовательность называется минимизирующей для функционала (6.25).
Каждое приближённое решение из этой последовательности разыскивается «прямым методом». Для этого используется линейная аппроксимация (6.4), которая и подставляется в (6.9). При этом функционал преобразуется в функцию нескольких переменных  , для которой необходимо разыскать минимум, то-есть, такие значения
, для которой необходимо разыскать минимум, то-есть, такие значения 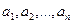 , при которых эта функция приобретает минимум. Эта задача в принципиальном плане легко выполнима и изучалась в курсе прикладной математики. Её решение осуществляется в два этапа - 1) поиск стационарных (иначе - критических) точек и 2) проверка выполнения достаточных условий наличия минимума. В большинстве случаев (например, если возможность потери устойчивости сжатыми стержнями исключена) второй этап излишен - стационарная точка единственна и является точкой минимума.
, при которых эта функция приобретает минимум. Эта задача в принципиальном плане легко выполнима и изучалась в курсе прикладной математики. Её решение осуществляется в два этапа - 1) поиск стационарных (иначе - критических) точек и 2) проверка выполнения достаточных условий наличия минимума. В большинстве случаев (например, если возможность потери устойчивости сжатыми стержнями исключена) второй этап излишен - стационарная точка единственна и является точкой минимума.
Поиск стационарной точки функции  сводится к её дифференцированию (а для линейной задачи она является квадратичной формой), приравниванию производных нулю и решению полученной системы линейных алгебраических уравнений. Дифференцирование квадратичных форм выполняется элементарно в общем виде, что будет продемострировано ниже; решение системы линейных алгебраических уравнений прекрасно обеспечено компьютерными программами.
сводится к её дифференцированию (а для линейной задачи она является квадратичной формой), приравниванию производных нулю и решению полученной системы линейных алгебраических уравнений. Дифференцирование квадратичных форм выполняется элементарно в общем виде, что будет продемострировано ниже; решение системы линейных алгебраических уравнений прекрасно обеспечено компьютерными программами.
Рассмотрим процедуру подстановки аппроксимации в уравнение (6.9) подробнее:

 ; (6.28)
; (6.28)

=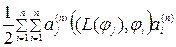 . (6.29)
. (6.29)
Из (6.29) ясно, почему мы наложили на 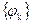 условие
условие 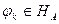 : это условие означает, что должно существовать скалярное энергетическое произведение
: это условие означает, что должно существовать скалярное энергетическое произведение  при заданных краевых условиях (как минимум - главных краевых условиях). Само это произведение, будучи по определению равно определённому интегралу от произведения функций
при заданных краевых условиях (как минимум - главных краевых условиях). Само это произведение, будучи по определению равно определённому интегралу от произведения функций  и
и 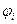 , равно постоянной величине; обозначим её
, равно постоянной величине; обозначим её  :
:
 . (6.30)
. (6.30)
При однородных краевых условиях (когда  , то-есть, все координатные функции тоже удовлетворяют этим условиям)
, то-есть, все координатные функции тоже удовлетворяют этим условиям)  .
.
На основании теоремы о взаимности работ 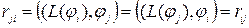 . Таким образом, при однородных главных краевых условиях матрица
. Таким образом, при однородных главных краевых условиях матрица  симметрична и положительна. Она называется матрицей Ритца.
симметрична и положительна. Она называется матрицей Ритца.
Если координатные функции таковы, что собственные значения матрицы Ритца ограничены снизу и сверху величинами, не зависящими от количества функций в координатной системе, то, как указывалось выше, вычисления будут устойчивыми к погрешностям вычислений.
Теперь на основании (6.29), (6.30) мы можем записать приближённое выражение для функционала (6.26) на линейной аппроксимации (6.4)
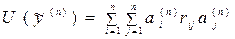 . (6.31)
. (6.31)
Это положительно определённая квадратичная форма коэффициентов  с симметричной матрицей.
с симметричной матрицей.
Аналогично приближённое значение функционала (6.27) на (6.4)
 , (6.32)
, (6.32)
где 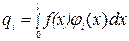 .
.
Окончательно значение функционала аппроксимации согласно (6.25)
 . (6.33)
. (6.33)
Необходимое условие стационарности (6.33), как функции  переменных, на искомой аппроксимации
переменных, на искомой аппроксимации
 . (6.34)
. (6.34)
При выводе (6.34) было учтено, что
1)  и слагаемые
и слагаемые  повторяются дважды, так как
повторяются дважды, так как
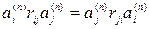 ;
;
2)  .
.
Таким образом, определение коэффициентов линейной аппроксимации заключается в решении системы линейных уравнений  -го порядка. Можно доказать, что если система
-го порядка. Можно доказать, что если система 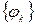 линейно независима, то определитель системы уравнений (6.34) не равен нулю и вектор
линейно независима, то определитель системы уравнений (6.34) не равен нулю и вектор 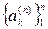 существует и единствен. Её решение существенно упрощается благодаря симметрии матрицы Ритца. Доказано, что при предположениях, сформулированных в этой лекции, последовательность
существует и единствен. Её решение существенно упрощается благодаря симметрии матрицы Ритца. Доказано, что при предположениях, сформулированных в этой лекции, последовательность  с коэффициентами, определёнными при каждом
с коэффициентами, определёнными при каждом  методом Ритца, является минимизирующей для функционала (6.25), то-есть,
методом Ритца, является минимизирующей для функционала (6.25), то-есть,  , где
, где 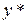 - точное решение исходной задачи.
- точное решение исходной задачи.
|

Метод Бубнова-Галёркина. Рассмотрим первоначальный наиболее простой вариант этого метода. Он может быть применён при гораздо более слабых ограничениях на оператор задачи; в частности, он не требует, чтобы этот оператор был положительным.
Введём понятие невязки уравнения 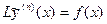 для решения
для решения  , где
, где 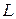 - оператор (в рамках нашего курса – дифференциальный), а именно, назовём его невязкой функцию
- оператор (в рамках нашего курса – дифференциальный), а именно, назовём его невязкой функцию
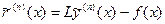 . (6.35)
. (6.35)
Так как  то и
то и 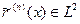 .
.
При подстановке в уравнение точного решения 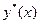 невязка равна нулю
невязка равна нулю
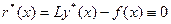 . (6.36)
. (6.36)
Пространство 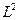 сепарабельно, поэтому в нём можно указать счётную систему координатных функций
сепарабельно, поэтому в нём можно указать счётную систему координатных функций 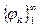 , образующих базис. Как установлено в функциональном анализе, нулевой элемент должен быть ортогональным ко всем элементам базиса. Если мы используем приближённое решение, то оно должно быть элементом наилучшего приближения в подпространстве
, образующих базис. Как установлено в функциональном анализе, нулевой элемент должен быть ортогональным ко всем элементам базиса. Если мы используем приближённое решение, то оно должно быть элементом наилучшего приближения в подпространстве  , натянутом на «усечённую» координатную систему
, натянутом на «усечённую» координатную систему  . Как можно доказать, это проекция точного решения на указанное подпространство, следовательно, невязка должна быть ортогональна к нему. Это обеспечивается ортогональностью невязки ко всем
. Как можно доказать, это проекция точного решения на указанное подпространство, следовательно, невязка должна быть ортогональна к нему. Это обеспечивается ортогональностью невязки ко всем 
 . (6.37)
. (6.37)
По аналогии с (6.28), (6.29)
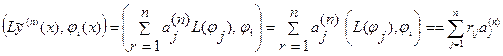 . (6.38)
. (6.38)
Обозначим
 (6.39)
(6.39)
Подставив (6.38), (6.39) в (6.37) и перенеся 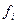 в правую часть, получим условия ортогональности невязки к базису подпространства
в правую часть, получим условия ортогональности невязки к базису подпространства 
 (6.40)
(6.40)
Это система линейных алгебраических уравнений 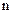 -го порядка относительно коэффициентов
-го порядка относительно коэффициентов 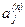 . Если координатные функции линейно независимы, то её матрица - неособенная, она имеет решение и притом единственное.
. Если координатные функции линейно независимы, то её матрица - неособенная, она имеет решение и притом единственное.
Если оператор задачи положителен и симметричен, а дифференциальное уравнение имеет решение и притом единственное, то эта матрица совпадает с матрицей Ритца и оба метода приводят к одному и тому же результату. Преимущество метода Бубнова-Галёркина заключается в том, что он имеет более широкую область применения.
По мере увеличения размерности подпространства  невязка становится ортогональной ко всё большему количеству элементов базиса исходного пространства
невязка становится ортогональной ко всё большему количеству элементов базиса исходного пространства 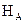 ; при соблюдении всех отмеченных выше требований к
; при соблюдении всех отмеченных выше требований к 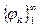 невязка будет всё «ближе» к тождественному нулю, а приближённое решение будет стремиться к точному
невязка будет всё «ближе» к тождественному нулю, а приближённое решение будет стремиться к точному
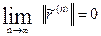 , (6.41)
, (6.41)
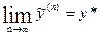 . (6.42)
. (6.42)
|

1. Необходимость многократного выполнения расчёта. Иногда при использовании приближённых методов, основанных на представлении искомой функции конечной линейной комбинацией координатных функций, расчётчики ограничиваются однократным расчётом при выбранном заранее количестве координатных функций. Это допустимо только при наличии каких-то предватрительных соображений, опыта расчёта подобных объектов, предварительной информации о характере решения(например, эмпирических данных). Конечно, в литературе встречаются оценки погрешности приближённых решений. Их можно разделить на априорные и апостериорные. Первые оценки выполняются до расчёта, но для их реализации обычно требуется такая информация о задаче или о её решении, которой расчётчик не располагает. Вторые осуществляются на основании результатов расчётов того же объекта с меньшим количеством координатных функций, то-есть,требуют неоднократного выполнения расчёта с увеличивающимся количеством координатных функций. Так как последовательность таких решений сходится, а пространство  полно, то любая сходящаяся в
полно, то любая сходящаяся в  последовательность фундаментальна, и достаточно прослеживать норму разности двух последовательных решений.
последовательность фундаментальна, и достаточно прослеживать норму разности двух последовательных решений.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1042; Нарушение авторских прав?; Мы поможем в написании вашей работы!
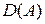 (для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.
Вернитесь к тексту
(для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.
Вернитесь к тексту