Лекция 1. Требования к математическим моделям

План лекции

1. Требования адекватности, точности, экономичности.

2. Области адекватности модели.

3. Иерархия математических моделей в САПР.

4. Уравнения полной модели и макромодели.

5. Микро-, макро- и метауровни.

Основными требованиями к математическим моделям являются требования адекватности, точности, экономичности.

Модель всегда лишь приближенно отражает некоторые свойства объекта. Адекватность имеет место, если модель отражает заданные свойства объекта с приемлемой точностью. Под точностью понимают степень соответствия оценок одноименных свойств объекта и модели.

Адекватность оценивается перечнем отражаемых свойств и областями адекватности. Область адекватности – область в пространстве параметров, в пределах которой погрешности модели остаются в допустимых пределах.

Пусть относительная погрешность модели по -му выходному параметру:

,

где 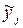– -й выходной параметр, рассчитанный с помощью модели; – тот же параметр, имеющий место в моделируемом объекте.

Погрешность модели по совокупности учитываемых выходных параметров оценивается одной из норм вектора , например

или .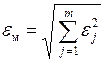

Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. Если задаться предельно допустимой погрешностью 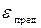, то можно в пространстве внешних параметров выделить область, в которой выполняется условие

.

Эту область называют областью адекватности (ОА) модели. Возможно введение индивидуальных предельных значений для каждого выходного параметра и определение ОА как области, в которой одновременно выполняются все 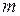условий вида .

Пример ОА (заштрихована) в двумерном пространстве дан на рисунке. Здесь 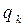– 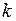-й внешний параметр.

Определение областей адекватности для конкретных моделей - сложная процедура, требующая больших вычислительных затрат. Эти затраты и трудности представления ОА быстро растут с увеличением размерности пространства параметров. Определение ОА – более трудная задача, чем, например, задача параметрической оптимизации, поэтому для моделей вновь проектируемых объектов ОА не рассчитывают.

Однако для моделей унифицированных элементов расчет областей адекватности становится оправданным в связи с однократностью определения ОА и многократностью их использования при проектировании различных систем. Знание ОА позволяет правильно выбирать модели элементов из числа имеющихся и тем самым повышать достоверность результатов машинных расчетов.

В общем случае ОА может иметь произвольную форму, сведения о которой выражаются громоздко, и неудобна в использовании, поэтому на практике вместо истинных ОА применяют те или иные их аппроксимации. Наиболее просто представляются и используются сведения об областях, имеющих форму гиперпараллелепипеда, который задается 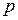двусторонними неравенствами:

,

где 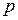- размерность пространства внешних параметров.

Так для одной из возможных макромоделей логического элемента транзисторно-транзисторной логики, реализующего функцию И-НЕ, рассчитанная область адекватности выражается следующими неравенствами:

где 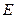– напряжения питания; – длительность фронта входного сигнала; 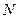- коэффициент нагружения; – длительность входного сигнала.

В библиотеку моделей элементов наряду с алгоритмом, реализующим модель, и номинальными значениями параметров должны включаться граничные значения внешних параметров и 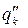, задающие область адекватности.

На рисунке дано графическое представление области адекватности и аппроксимирующего ее гиперпараллелепипеда. Такое представление удобно для двумерных случаев.

Возможно использование и других аппроксимаций ОА, например областей с линеаризованными границами в виде гиперплоскостей, областей в форме гиперсфер и т.п.

Экономичность (вычислительная эффективность) определяется затратами ресурсов, требуемых для реализации модели. Поскольку в САПР используются математические модели, далее речь пойдет о характеристиках именно математических моделей, и экономичность будет характеризоваться затратами машинных времени и памяти.

Аналогичные требования по точности и экономичности фигурируют при выборе численных методов решения уравнений модели.

ИЕРАРХИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ В САПР

Блочно-иерархический подход к проектированию РЭА включает в качестве своей основы иерархию математических моделей. Деление моделей по иерархическим уровням (уровням абстрагирования) происходит по степени детализации описываемых свойств и процессов, протекающих в объекте. При этом на каждом иерархическом уровне используют свои понятия “система” и “элементы”. Так система 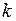-го уровня рассматривается как элемент на соседнем более высоком -м уровне абстрагирования.

Представим структуру некоторого объекта в виде множества элементов (рис. 4.1) и связей между ними.

Рис. 1. Представление структуры объекта

Выделим в соответствии с блочно-иерархическим подходом в структуре объекта некоторые подмножества элементов и назовем их блоками (на рисунке показаны штриховыми линиями). Пусть состояние каждой связи характеризуется одной фазовой переменной , или 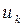. Здесь относится к внутренним связям между элементами данного блока, , 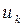относятся к выходам и входам блока соответственно. Теперь поясним важные для функциональных моделей понятия полной модели и макромодели.

Полная модель блокаесть модель, составленная из моделей элементов с учетом межэлементных связей, т.е. модель, описывающая как состояние выходов, так и состояние каждого из элементов блока. Моделями элементов блока 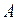являются уравнения, связывающие входные и выходные переменные:

(1)

Полная модель блока есть система уравнений

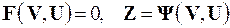, (2)

где – векторы внутренних, выходных и входных переменных блока.

При большом количестве элементов размерность вектора 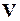и порядок системы уравнений (2) становится чрезмерно большим и требуются упрощения.

При переходе к более высокому иерархическому уровню упрощения основаны на исключении из модели вектора внутренних переменных 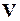. Полученная модель представляет собой систему уравнений

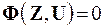(3)

существенно меньшей размерности, чем полная модель (2), и называется макромоделью. Следовательно, макромодель уже не описывает процессы внутри блока, а характеризует только процессы взаимодействия данного блока с другими в составе системы блоков.

Модели (2) и (3) относятся друг к другу как полная модель и макромодель на -м уровне иерархии. На более высоком 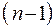-м уровне блок 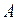рассматривается как элемент и макромодель (3) становится моделью элемента 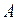. Следовательно, модели (1) и (3) относятся друг к другу как модели элементов соседних иерархических уровней. Из моделей типа (3) может быть составлена полная модель системы на 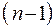-м уровне.

Микро-, макро- и метауровни. В зависимости от сложности объекта при его проектировании используют большее или меньшее число уровней абстракции. Объединение уровней, родственных по характеру используемого математического аппарата, приводит к образованию трех укрупненных уровней – микро-, макро- и метауровня – в иерархии функциональных моделей для большинства проектируемых сложных объектов.

На микроуровне используют математические модели, описывающие физическое состояние и процессы в сплошных средах. Для моделирования применяют аппарат уравнений математической физики. Примерами таких уравнений служат дифференциальные уравнения в частных производных – уравнения электродинамики, теплопроводности, упругости, газовой динамики. Эти уравнения описывают поля электрического потенциала и температуры в полупроводниковых кристаллах интегральных схем, напряженно-деформированное состояние деталей механических конструкций и т.п. К типичным фазовым переменным на микроуровне относятся электрические потенциалы, давления, температуры, концентрации частиц, плотности токов, механические напряжения и деформации. Независимыми переменными являются время и пространственные координаты. В качестве операторов 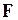и 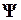в уравнениях (2) фигурируют дифференциальные интегральные операторы. Уравнения (2), дополненные краевыми условиями, составляют ММ объектов на микроуровне. Анализ таких моделей сводится к решению краевых задач математической физики.

На макроуровне производится дискретизация пространств с выделением в качестве элементов отдельных деталей, дискретных радиоэлементов, участков полупроводниковых кристаллов. При этом из числа независимых переменных исключают пространственные координаты. Функциональные модели на макроуровне представляют собой системы алгебраических или обыкновенных дифференциальных уравнений, для их получения и решения используют соответствующие численные методы. В качестве фазовых переменных фигурируют электрические напряжения, токи, силы, скорости, температуры, расходы и т.д. Они характеризуют проявления внешних свойств элементов при их взаимодействии между собой и внешней средой в электронных схемах или механических конструкциях.

На метауровне с помощью дальнейшего абстрагирования от характера физических процессов удается получить приемлемое по сложности описание информационных процессов, протекающих в проектируемых объектах. НА метауровне для моделирования аналоговой РЭА широко применяют аппарат анализа систем автоматического управления, а для моделирования цифровой РЭА – математическую логику, теорию конечных автоматов, теорию массового обслуживания. Математические модели на метауровне – системы обыкновенных дифференциальных уравнений, системы логических уравнений, имитационные модели систем массового обслуживания.

Список литературы:

1. Норенков И.П. Основы автоматизированного проектирования. – М.: Изд-во МГТУ им. Н.Э. Баумана. 2006.

2. В.П. Корячко, В.М. Курейчик, И.П. Норенков. Теоретические основы САПР – М.: Энергоатомиздат, 1987.

3. Феллер В. Введение в теорию вероятностей и ее приложения. Т. 1. – М.: Мир, 1984.

4. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения – М.: Высш. шк., 2007.

5. Авен О.И., Гурин Н.Н., Коган Я.А. Оценка качества и оптимизация вычислительных систем. – М., "Наука", Главная редакция физико-математической литературы, 1982. – 464 с.

6. Клейнрок Л. Теория массового обслуживания. – М.: Машиностроение, 1979 г. – 432 с.

7. Бертсекас Д., Галлагер Р. Сети передачи данных: Пер с англ. – М.: Мир, 1989. 544 с.

Дата добавления: 2014-01-20