Числовые характеристики случайных непрерывных величин

Математическим ожиданием случайной непрерывной величины Х, возможные значения которой принадлежат всей оси Ох ]-¥ < x < +¥], называется несобственный интеграл

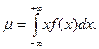
Если возможные значения Х принадлежат отрезку [ a, b ], то

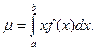(8)

Дисперсией непрерывной случайной величины, возможные значения которой принадлежат всей оси Ох, называют несобственный интеграл

Если возможные значения принадлежат отрезку [ a, b ], то дисперсия

Для вычисления дисперсии случайных непрерывных величин пользуются более удобными формулами:

(9)

Среднее квадратичное отклонение непрерывной случайной величины

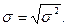
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ (ЗАКОН ГАУССА).

Наиболее часто встречаются случайные величины, распределенные по нормальному закону, или по закону Гаусса. Главная особенность, выделяющая нормальный закон среди других законов распределения, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при часто встречающихся типичных условиях.

Случайная величина распределена по нормальному закону, если плотность вероятности ее имеет вид

(10)

где m = М{Х} - математическое ожидание случайной величины; s - среднее квадратическое отклонение нормально распределенной случайной величины;

f(x) выражает плотность вероятности случайной величины. Часто вместо параметра s вводят параметр , который называют мерой точности. В этом случае плотность вероятности нормального распределения имеет вид

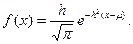
График плотности вероятности нормально распределенной случайной величины (10) приведен на рис.1 и носит название нормальной кривой

Рис.1.

распределения или кривой Гаусса. Как видно из рис.1, функция f(x) определена на всей оси Ох, при всех значениях х f(x)>0, при |х|®¥ 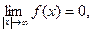то есть ось Ох служит горизонтальной асимптотой графика. В точке х = m функция имеет максимум 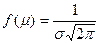, то есть математическое ожидание случайной величины является наивероятнейшим ее значением. Точки В и С являются точками перегиба.

Установим, как влияют параметры m и s на форму кривой Гаусса.

Из формулы (10) видно, что центром симметрии распределения является центр рассеяния х = m и, если изменять центр рассеяния m, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы. Таким образом, математическое ожидание случайной величины m определяет

Рис.2. Рис.3.

положение распределения на оси абсцисс (рис. 2). При m = 0 (рис. 3)

1. Параметр s определяет форму кривой распределения (рис.3). Максимум функции нормального распределения при х = m равен

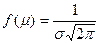
Вероятность попадания в заданный интервал нормально распределенной случайной величины.

Вероятность попадания случайной величины Х в интервал значений х, заключенный между числами х₁ и х₂ равна

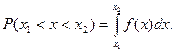
Для нормально распределенной случайной величины, согласно формуле (10),

и вероятность попадания в заданный интервал ]х₁, х₂[ нормально распределенной случайной величины

(11)

Вероятность того, что случайная нормально распределенная величина Х попадает в интервал значений m-s < х < m+s, будет равна

Вероятность того, что случайная величина Х попадает в интервал значений (m-2s < х < m+2s), равна

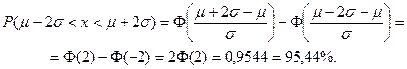
Вероятность того, что случайная величина попадает в интервал значений (m-3s < х < m+3s), равна

Расчеты показывают, что случайная величина, распределенная по нормальному закону, практически не отклонится от центра распределения m более чем на 3s, ибо вероятность нахождения ее в интервале значений ] m-3s < х < m+3s [ равна 0,9971 @ 1, а это соответствует практической достоверности. Иными словами, вероятность того, что отклонение по абсолютной величине превысит утроенное среднее квадратическое отклонение, очень мала, а именно: равна 0,0028. Исходя из принципа невозможности маловероятных событий, такие события можно считать практически невозможными. В этом и состоит сущность правила «трех сигм», которое можно сформулировать так.

Если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине не превосходит утроенного среднего квадратического отклонения.

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТА:

Из 982 больных, поступивших в хирургическую больницу за месяц, 275 человек имели травмы. Какова относительная частота поступления с этим видом заболевания?

САМОКОНТРОЛЬ УСВОЕНИЯ ТЕМЫ:

Вызов врача на дом оценивается вероятностью 0,4. Найти вероятность того, что из пяти вызовов врача два вызова будут в данный дом.

ЛИТЕРАТУРА

1. Лобоцкая Н.Л. Основы высшей математики - М.: «Вышэйшая школа», 1978. С299-355.

2. Бейли Н. Математика в биологии и медицине. Пер. с англ. М.: «Мир», 1970.

3. Ремизов А.Н., Исакова Н.Х., Максина Л.Г. Сборник задач по медицинской и биологической физике – М.: «Высшая школа», 1987. С23-28.

Дата добавления: 2014-01-20