Постановка задачи. Классические задачи математического программирования

Классические задачи математического программирования

Так называется задача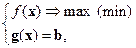

отыскания глобального экстремума целевой функции нескольких (n) переменных 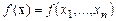при m условиях связи (1 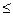m <n), накладываемых на эти переменные:

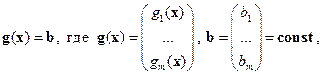т.е. .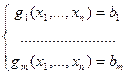

В этом случае допустимое множество задачи имеет вид .

Так же, как и при рассмотрении задач безусловной оптимизации, будем считать, что область определения функци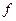й и совпадает со всем пространством 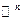. Если же в области определения функци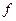й или появляются граничные точки, будем относить эти задачи к задачам нелинейного программирования. А причины возникновения границ будем искать в существе рассматриваемой экономической задачи, что в математической модели должно выражаться в виде наличия соответствующих ограничений.

Всюду далее будем предполагать, что 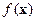и 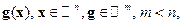– дважды непрерывно дифференцируемые функции в своей области определения.

Наглядное представление об условном экстремуме и его отличии от безусловного может дать следующий наглядный пример. Предположим, что мы идем по тропинке на склоне горы в направлении, указанном стрелкой (рис. 4). Проекция тропинки на горизонтальную плоскость представляет собой некоторую линию . Когда мы идем по тропинке, проекция нашего положения на ней перемещается вдоль этой линии. Слева от тропинки поверхность горы поднимается вверх, справа – опускается вниз. Целевая функция 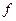– высота нашего положения над уровнем моря. Сама тропинка идет то вниз, то вверх в зависимости от рельефа горы. Вершина горы находится в точке – это наивысшая точка. На горизонтальной плоскости ей соответствует точка безусловного экстремума функции 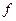. Но нас интересует только тропинка. 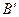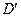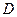Если мы спускаемся вниз по ней, а затем поднимаемся вверх, то в точках и , где спуск сменяется подъемом (точки и на тропинке), располагается точка условного минимума. А в точке , в которой подъем сменяется спуском (точка на тропинке), располагается точка условного максимума. Условного – потому что нашим условием является рассмотрение только точек, находящихся на линии , т.е. когда мы находимся на тропинке. Нас совершенно не интересует, что находится слева и справа от нее, хотя слева всегда есть точки и повыше, а справа – пониже, чем на тропинке.

Рис. 4. Наглядная иллюстрация понятия условного экстремума

Замечание 1. В классической задаче математического программирования рассматривается случай, когда число связей меньше n, поскольку, как правило, введение каждой новой связи ведет к уменьшению размерности задачи на единицу. Таким образом, уже при n связях размерность задачи (допустимого множества), как правило, была бы равна нулю (отдельные точки), а при большем числе связей допустимое множество вообще будет пустым. Хотя возможны исключения и в ту, и в другую стороны: при размерность допустимого множества может оказаться положительной, а при допустимое множество может оказаться пустым.

Замечание 2. Рассматриваемые далее методы решения классической задачи математического программирования предполагают поиск локальных экстремумов во внутренних точках общей области определения целевой функции и всех функций связи . Разумеется, что при этом рассматриваемые точки должны удовлетворять условиям связи

Глобальный экстремум (если он существует) следует искать среди точек локального экстремума. Однако напомним, что глобальный максимум (наибольшее значение) и глобальный минимум (наименьшее значение) могут не существовать, несмотря на наличие локальных экстремумов. Из этого следует, что прежде, чем искать глобальный экстремум, нужно убедиться в его существовании.

В простейших случаях задача отыскания точек локального условного экстремума может быть решена методом исключения переменных: часть переменных выражается из условий связи (решается система) и полученные выражения подставляются в целевую функцию – см. примеры 1 – 3. Данный метод наиболее прост для использования, когда условия связи представляют собой линейные уравнения (системы).

Дата добавления: 2014-01-20