Признаки условного локального экстремума

Пример

Найти точки условного экстремума и экстремальные значения функции 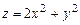при условии .

В более сложных случаях (когда решение системы затруднено) отыскание точек локального условного экстремума может быть осуществлено методом Лагранжа. Метод Лагранжа основывается на использовании вспомогательной функции, называемой функцией Лагранжа, или лагранжианом: 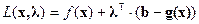, или в скалярной записи:

.

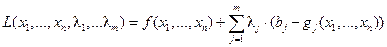Компоненты вектора называются множителями Лагранжа.

Очевидно, при выполнении условия связи 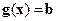(т.е. всюду на допустимом множестве) значения функции Лагранжа не зависят от и совпадают со значениями целевой функции: 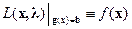. Таким образом, задача нахождения условного максимума (минимума) функции 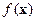эквивалентна задаче нахождения (условного же!) максимума (минимума) функции 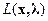при том же условии связи 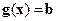на переменные .

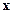Выведем необходимые, а также достаточные условия существования условного локального экстремума. При этом будем предполагать. Что мы имеем дело с внутренней точкой общей области определения функци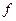й и 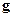. Вначале на примере функции двух переменных при одном условии связи будет продемонстрирована идея вывода, а затем сформулирована соответствующая теорема.

4.2.1. Идея вывода необходимого условия I порядка. Продемонстрируем идею вывода необходимого условия I порядка для функции двух переменных и одного уравнения связи: 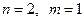, поскольку этот случай допускает наглядную графическую иллюстрацию. Тогда задача примет вид: найти локальные экстремумы функции при условии связи .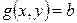

В типичном случае условие связи представляет собой некоторую кривую на плоскости (линию уровня функции ) – рис. 5. Градиент функции (если он не нулевой!) направлен, как известно, перпендикулярно к линии уровня (в одну из двух сторон). Посмотрим, какое направление может иметь градиент целевой функции 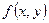в точке экстремума.

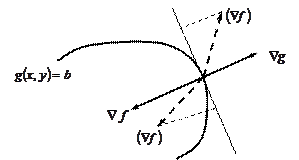Рис. 5. Соотношение возможных и невозможных (приведены в скобках) направлений градиентов целевой функции и функции, описывающей условие связи, в точке экстремума

Нетрудно видеть, что если направлен под углом к 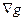(не равным нулю и 180⁰), то ни максимума, ни минимума в рассматриваемой точке быть не может, поскольку в этом случае в одном из направлений вдоль линии уровня 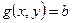целевая функция будет возрастать, а в противоположном – убывать. Таким образом, обязан быть коллинеарным с 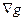. А это означает, что существует некоторое (положительное, отрицательное или даже нулевое – если = 0) число 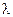такое, что .

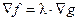Последнее равенство можно представить в виде:

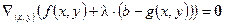, или ,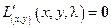

где обозначает градиент функции по переменным 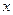и 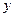(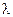считается параметром, т.е. константой).

Очевидно, условие коллинеарности градиентов: 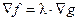может выполняться не только на линии уровня 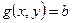, но и на других линиях уровня вида 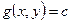. Поэтому, чтобы исключить такие лишние решения уравнения, к нему целесообразно добавить условие принадлежности точки допустимому множеству: 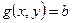. Это условие, очевидно, можно записать как 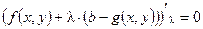, или как

.

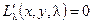Это также является одним из необходимых условий. Собирая вместе условия и, получим новое необходимое условие – систему уравнений для нахождения точек, подозрительных на условный локальный экстремум:

.

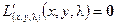При решении системы (4) мы находим не только «подозрительные» точки , но и множители Лагранжа 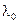, которые, вообще говоря, не имеют отношения к конечной цели решения математической задачи – нахождения точек условного экстремума. Однако, как мы увидим в дальнейшем, множители Лагранжа играют важную роль в экономических задачах.

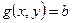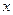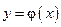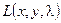Обратим внимание на то, что в левой части уравнения стоит градиент функции Лагранжа от трех переменных, причем формально никаких условий связи на переменные х и у не накладывается. Это означает, что при вычислении этого градиента не нужно решать уравнение относительно, у или , т.е. находить функцию или и подставлять ее в . Таким образом, решение уравнения дает нам множество безусловных стационарных точек функции Лагранжа. В этом и состоит главное достоинство и смысл метода Лагранжа.

Безусловность стационарных точек означает, что они ищутся в пространстве 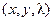без учета (в явном виде) условия связи переменных 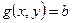, т.е. при вычислении частных производных все переменные считаются независимыми. Условия связи 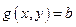, как уже отмечалось, учитывается при решении системы (4), в которую входит, в частности, уравнение 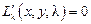, что равносильно этому условию связи. Тем самым гарантируется, что при решении системы (4) мы получим только точки из допустимого множества.

4.2.2. Условие Якоби. Единственным ограничением, которое мы наложили при выводе данного необходимого условия, является неравенство нулю градиента функции . Это ограничение называется условием Якоби. Очевидно, если условие Якоби не выполняется, то не удастся подобрать такого 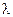, чтобы выполнялось равенство 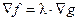(за исключением случая 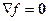). Для случая большего числа ограничений условие Якоби выглядит как линейная независимость градиентов 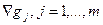. Покажем, что требование выполнения условия Якоби существенно, т.е. при его нарушении условие первого порядка (4) не является необходимым.

Дата добавления: 2014-01-20