Теорема. Пусть требуется отыскать условный экстремум функции при условии связи (рис.5)

Пример

Пусть требуется отыскать условный экстремум функции 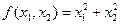при условии связи 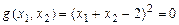(рис.5).

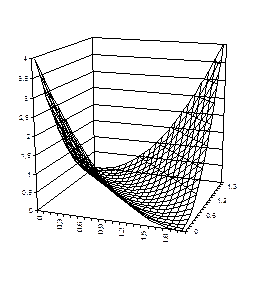
а) б)

Рис. 6. Иллюстрация к примеру 1: а) функция, задающая условие связи; жирной прямой линией показано допустимое множество; б) целевая функция: жирной кривой линией показан график целевой функции в пределах допустимого множества

Решая эту задачу методом исключения переменной: , получим:

.

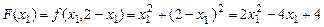Эта функция, очевидно, имеет минимум в точке 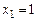, а значит, функция f при указанном условии связи имеет минимум в точке (1;1). Значение целевой функции в точке минимума.

Попробуем решить эту задачу методом Лагранжа.

Составим функцию Лагранжа: .

Выпишем необходимые условия первого порядка:

Из последнего равенства получаем 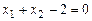. С учетом этого, из первого равенства имеем 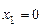, а из второго: 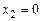. Возвращаясь к третьему, получим: 4 = 0, т.е. система несовместна. Таким образом, в данном случае метод Лагранжа не выявил точку условного минимума.

В чем причина? А причина, оказывается, в том, что в этой точке (как, впрочем, и на всем допустимом множестве ) градиент функции g равен нулю, т.е. условие Якоби не выполняется:

.

Как быть в таком случае?

В данном случае видно, что, не изменяя существа задачи (допустимого множества), можно упростить условие связи, т.е. вместо заданного взять эквивалентное ему: .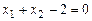

В этом случае градиент не обращается в нуль нигде, и метод Лагранжа дает: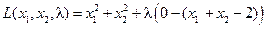

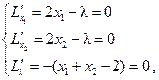
откуда 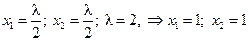, т.е. в этом случае потери стационарной точки не происходит.

В данном случае указанное выше упрощение условия связи очевидно. Однако так обстоит дело далеко не всегда. Даже в этом примере, если в условии связи раскрыть скобки, не сразу видно, как упростить выражение .

Как уже говорилось, в общем случае ограничений

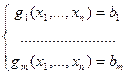
выполнение условия Якоби в точке 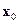означает, что градиенты функций 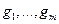линейно независимы, т.е. не существует нетривиальной линейной комбинации .

Это равносильно тому, что матрица частных производных этих функций имеет в точке 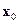ранг (т.е. матрица полного ранга):

.

4.2.3. Идея вывода условий II порядка. Проиллюстрируем вывод необходимого условия II порядка и достаточного условия. Будем при этом считать, что необходимое условие I порядка уже обосновано. Оно войдет, естественно, и в общее необходимое условие, и в достаточное условие.

Воспользуемся тем же приемом, которым мы доказывали необходимое и достаточное условия для безусловного экстремума – разложением по формуле Тейлора. Однако в данном случае мы будем раскладывать не целевую функцию, а функцию Лагранжа (которая на допустимом множестве совпадает с целевой функцией) и учитывать, что ее максимум рассматривается не во всей окрестности, а лишь на допустимом множестве .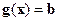

Доказательство будем проводить для условного локального максимума. Для доказательства теоремы о минимуме достаточно рассмотреть функцию , применить к ней теорему о максимуме и затем «пересчитать» полученные соотношения для .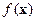

Будем предполагать, что 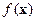и 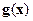– дважды непрерывно дифференцируемые функции в некоторой окрестности точки 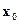Очевидно, таким же свойством обладает и функция . Таким образом, в некоторой (полной) окрестности 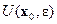, т.е. для , можно написать разложение по формуле Тейлора до членов второго порядка включительно:

,

или, так как : .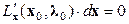

В соответствии с определением условного локального максимума необходимо и достаточно, чтобы в некоторой окрестности 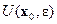рассматриваемой точки 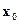для любого 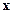, для которого 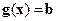, выполнялось условие: 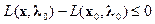, т.е.

(для строгого максимума – знак неравенства строгий: "<" при ).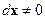

Итак, наличие условного локального максимума в точке 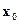эквивалентно выполнению условия. Применяя рассуждения, аналогичные тем, что использовались для безусловного экстремума, можно показать, что из вытекает 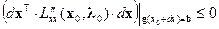– для необходимости и 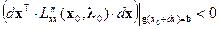– для достаточности.

Более тонкий анализ показывает, что условие может быть заменено на более удобное для использования линейное условие .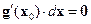

Проиллюстрируем существо отличия векторов 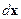в условиях и 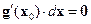. В первом случае берутся такие векторы 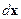, что точки 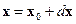принадлежат допустимому множеству. Во втором случае вектор 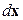направлен по касательной к поверхности уровня 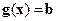(он перпендикулярен ко всем градиентам ) – рис. 7. Ясно, что когда , вектор 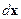из условия будет стремиться к вектору 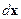из условия .

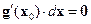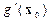
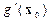
Рис. 7. Иллюстрация различия между векторами 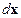в условиях (а)

и (б)

4.2.4. Теорема о признаках условного локального экстремума. Приведенные рассуждения приводят к следующей теореме.

Пустьи 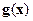– дважды дифференцируемые функции в некоторой окрестности рассматриваемой точк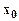и и .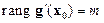

Тогда для наличия в точке 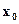условного локального максимума (минимума) целевой функции 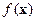при условии связи необходимо, чтобы существовал такой вектор , что

и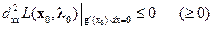

и достаточно (даже для строгого экстремума), чтобы существовал такой вектор , что

и .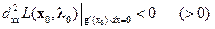

Замечание 1. Как уже отмечалось ранее, условие 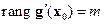называется условием Якоби. Его можно сформулировать следующим эквивалентным способом: градиенты функций связи линейно независимы в точке .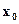

Точки, в которых условие Якоби не выполняется, могут быть потеряны при отыскании условного экстремума методом Лагранжа (см. пример 1). Поэтому их следует анализировать особо.

Замечание 2. Условие 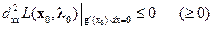означает, что второй дифференциал функции Лагранжа при любых значениях , подчиненных условию связи 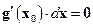, принимает неположительные (неотрицательные) значения. Напомним, что [2] что эквивалентно неположительной (неотрицательной) определенности окаймленной матрицы Гессе при дополнительном ограничении , где .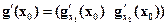

Аналогично, строгое неравенство в достаточных условиях эквивалентно отрицательной (положительной) определенности окаймленной матрицы Гессе .

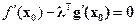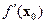Замечание 3. При сделанных в теореме предположениях (при выполнении условия Якоби) вектор , если он существует, определяется однозначно. Действительно, из уравнения следует: , или , т.е. градиент (вектор) представляет собой линейную комбинацию линейно независимых векторов 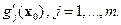Как известно, такое представление единственно.

Замечание 4. Из теоремы следует, что если в стационарной точке окаймленная матрица Гессе положительно (отрицательно) определена, то целевая функция имеет в данной точке минимум (максимум). Если неопределена (квадратичная форма от дифференциалов знакопеременна), – то экстремума нет, если же квазиопределена (полуопределена), - то данная теорема ответа не дает – требуется дополнительное исследование.

Дата добавления: 2014-01-20