Мостовые схемы

Потенциометрическая схема

Электрические цепи

Датчики изменяют свое сопротивление под воздействием внешней нагрузки по формуле:

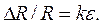(3.6)

Величина 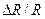может быть измерена двумя наиболее распространенными способами: мостовым и потенциометрическим.

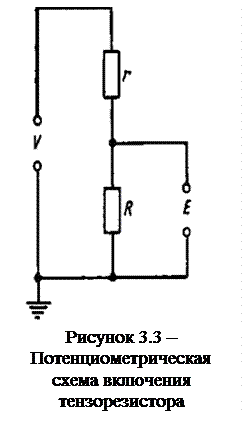
На рис. 3.3 представлена потенциометрическая схема включения тензодатчика в электрическую цепь, которая часто используется при изуче­нии динамических явлений и преобразует изменение сопротивления 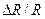в изменение напряжения 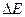. Здесь источник тока с на­пряжением V подключается к датчику R через добавочное балластное сопротивление r; изменение напряжения на датчике фикси­руется с помощью измерительного прибора. Когда сопротивление прибора приблизи­тельно в 100 раз превышает сопротивление тензорезистора, напряжение на датчике Е выражается следующей зависимостью:

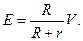(3.7)

Если сопротивление датчика вследствие деформации меняется на 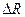, то напряжение на выходе будет равно:

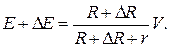(3.8)

Вычитая эти равенства, получим:

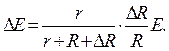(3.9)

Эта зависимость нелинейная, но при измерении деформаций менее 0,01 величиной 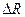в знаменателе можно пренебречь по сравнению с (R+r) и тогда ΔE будет прямо пропорциональна изменению сопротивления. При этом погрешность измерения деформаций не превышает 2 %. Из формулы (3.9) также видно, что увеличение балластного сопротивления приводит к улучшению линейной связи. Потенциометрический способ измерения обеспечивает достаточно надежное определение деформаций в пределах до 2-10 %. Чувствительность потенциометрической схемы опре­деляется по формуле:

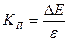. (3.10)

Величина K _п может быть интерпретирована как показатель качества или эффективности схемы; например, при изучении динамических процессов, когда измеряемые деформации, как правило, малы, чувствительность схемы должна достигать максималь­ных значений с тем, чтобы уменьшить степень усиления выход­ного сигнала.

На основании выражений (3.7 – 3.10) и закона Ома можно запи­сать:

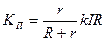, (3.11)

где k - коэффициент тензочувствительности датчика; I - сила тока в цепи.

Это уравнение показывает, что чувствительность цепи опре­деляется двумя независимыми параметрам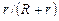и и 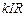. Первый из них определяется выбором балластного сопротивления r и в пределе приближается к единице, что соответствует максимальной эффективности. Однако при очень больших r тре­буется весьма высокое напряжение и поэтому на практике эту величину принимают равной 9R, при этом отношение 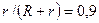. Второй параметр оказывает существенное влияние на чувствительность схемы и в зависимости от типа датчика и тока цепи может изменяться в пределах от 3 до 700. Изменение выход­ного напряжения датчиков обычно незначительно и поэтому K _п имеет порядок 5-10 В.

Большим достоинством потенциометрических схем является их простота, но в то же время они обладают рядом существенных недостатков. Изменение выходного напряжения ΔЕ весьма мало по сравнению с Е. Поэтому эта схема применяется главным образом для измерения динамических деформаций с использова­нием усилителей переменного тока, которые реагируют только на изменение ΔЕ. При изучении статических деформаций в схему необходимо вводить температурные компенсаторы. Так как вы­ход потенциометрической схемы ΔЕ прямо пропорционален на­пряжению источника питания V, то последний должен быть до­статочно стабильным. В качестве источника тока обычно исполь­зуются батареи.

Вторая схема, которая часто используется для регистрации изменений сопротивления датчика, представляет собой широко известный мостик Уитстона. Подобно потенциометрической схеме, мостик Уитстона применяется для изучения динамических и статических деформаций. Мостовая схема может быть использована для непосредственного считывания ∆ Е, ве­личина которого связана с деформацией, либо для измерений по методу сбалансированного моста (нулевой метод).

Рисунок 3.4 – Простейшая мостовая схема:   R₁ – рабочий датчик; R₂, R₃, R₄ – компенсационные датчики

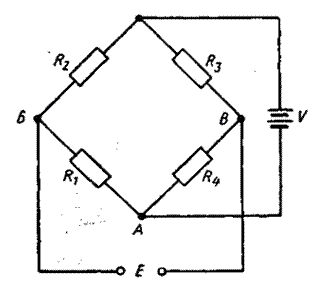
Простейшая мостовая схема представлена на рис. 3.4. Мостик составлен из четырех сопротивлений, из которых одно является датчиком и три - постоянными сопротивлениями; к одной диа­гонали мостика подведено питающее напряжение V, а к другой подключен регистрирующий прибор.

Выходное напряжение в этом случае опреде­ляется по формуле:

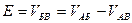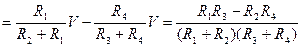= . (3.12)

Напряжение Е будет равно нулю и мостик находится в равновесии, когда

. (3.13)

Это свойство схемы используется для измерения деформаций; сначала мостик балансируется до Е = 0, после приложения внеш­ней нагрузки появляется разбаланс ∆ Е, который обусловлен изменением сопротивления датчика 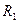. Напряжение выхода можно получить из выражений (3.12) и (3.13), пренебрегая членами второго порядка малости, и представить в виде:

. (3.14)

Это уравнение является базовым для оценки мостовой схемы. Так же, как и в случае потенциометрической схемы, нелиней­ностью данного уравнения можно пренебречь при измерении де­формаций менее 0,05.

Коэффициент чувствительности мостовой схемы определяется по формуле:

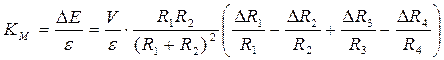. (3.15)

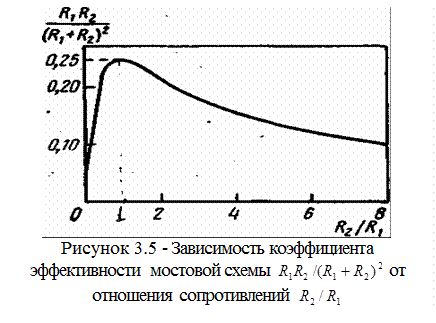Это выражение показывает, что чувствительность зависит от входного напряжения V, коэффициента чувствительности тензодатчика 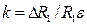и соотношения сопротивлени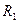й и 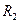. Из графика, представленного на рис. 3.5, видно, что при прочих равных условиях эффективность мостовой схемы является максимальной при =.

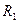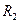Дата добавления: 2014-01-20