Производные различных порядков

Логарифмическое дифференцирование;

Лекция №8

Тема: Производные высших порядков и дифференциал

Вопросы:

1. Логарифмическое дифференцирование;

2. Производные различных порядков;

3. Дифференциал. Геометрическое значение дифференциала.

Дифференцирование различных функций значительно упрощается, если их предварительно прологарифмировать.

Допустим требуется найти из уравнения , то можно:

– прологарифмировать обе части уравнения по основанию ,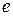

;

– продифференцировать обе части полученного равенства, как сложную функцию

– заменить его выражением .

Логарифмическое дифференцирование полезно применять, когда заданная функция содержит операции поддающиеся логарифмированию: умножение, деление, возведение в степень, извлечение корня.

Пример: Найти производную от функции 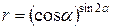. Решение:

1. ;

2. .

Пусть функция y=f(x) дифференцируема на некотором отрезке [a,b]. Значение первой производной f’(x), как отмечалось ранее, зависит от x, т.е. первая производная представляет собой тоже функцию от x. Дифференцируя эту функцию, можно получить вторую производную от функции f(x).

Производная от первой производной называется производной второго порядка или второй производной от первоначальной функции и обозначается символам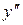и , или :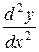

, .

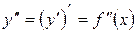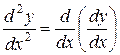Так, например, если y=x⁵, то , .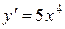

Производная от второй производной называется производной третьего порядка или третьей производной и обозначается символам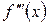и , или .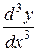

Вообще, производной n-го порядка от функции f(x) называется производная от производной (n-1) порядка и обозначается символами y⁽ⁿ⁾(x), f⁽ⁿ⁾(x) или :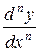

.

Пример. Дана функция (k=const). Найти выражение ее производной для любого порядка n.

Запишем , , .

Пример. Найти производную -го порядка для функции y=sinx.

Используя таблицу 1 функций и их производных, имеем

,

,

,

.

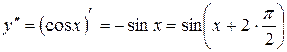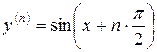Для производной n-го порядка, как и в случае первой производной, существуют простые правила, позволяющие выражать производную суммы и произведения конечного числа функций через производные своих функций.

Для производной n-го порядка функции y(x)=u(x)+v(x) можно записать очевидное выражение

,

т.е. n-я производная суммы двух функций равна сумме производных n-го порядка указанных функций.

Для производной n-го порядка от произведения двух функций 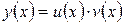существует формула Лейбница

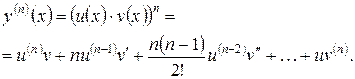
Пример. Найти производную n-го порядка для функции .

Положим 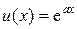, , тогда

, ;

, ;

, ;

, ;

....................

, .

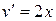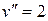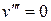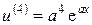Используя формулу Лейбница, получаем

.

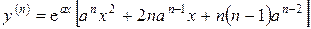Аналогичного соотношения, связывающего производную n-го порядка от частного двух функций с их производными (за исключением n=1) в общем виде не существует.

Дата добавления: 2014-01-20