
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Позиционные системы счисления
В позиционной системе счисления значение цифры зависит не только от ее вида, но и от ее местонахождения (позиции, разряда) в записи числа.
Каждой позиции (разряду) в записи числа можно присвоить номер, называемый номером разряда. При этом для указания начала отсчета используется символ «,», который всегда ставится на границе двух разрядов. Влево от него позиции нумеруются числами 0, 1, 2,…, а справа – числами -1, -2, -3,…
Если отношение количественного эквивалента некоторой цифры в i-м разряде к ее количественному эквиваленту в 0-м разряде постоянно для всех цифр, используемых системой, то это отношение называется весом i-го разряда. Система счисления, для которой каждый разряд имеет вес, называется весомозначной.
Если отношение веса i-го разряда к весу (i-1)-го разряда в весомозначной системе не зависит от значения i, то такая система называется естественной, а упомянутое отношение – её основанием. Естественная система полностью задается алфавитом используемых цифр, их количественным эквивалентом в любом фиксированном разряде (обычно нулевом) и значением основания. Действительно, на основе этих сведений легко можно подсчитать количественные эквиваленты цифр в коде произвольного числа, записанного в естественной системе, а затем и количественный эквивалент самого кода посредством суммирования количественных эквивалентов отдельных цифр.
Для большинства существующих систем количественный эквивалент кода числа есть сумма количественных эквивалентов цифр, составляющих этот код. Кроме того, известны так называемые мультипликативные системы, в которых суммирование количественных эквивалентов цифр заменяется их умножением.
Из приведенных выше определений легко понять, что степени основания играют в естественных системах роль весов разрядов. Нулевому разряду отвечает нулевая степень основания, т.е. вес нулевого разряда равен 1.
В зависимости от вида основания различают естественные системы счисления с натуральным, целым отрицательным, дробным и даже комплексным основаниями. Нас будут интересовать, в основном, естественные системы с натуральными основаниями, хотя ниже будет рассмотрена одна из систем с отрицательным основанием, а также весомозначные системы, не являющиеся естественными (двоично-десятичные системы), и один класс систем, не являющихся весомозначными (системы счисления в остаточных классах).
Легко понять, что код
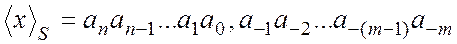
числа x в естественной системе с натуральным основанием S есть сокращенная запись количества
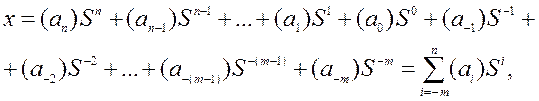 (3.1)
(3.1)
где 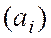 - количественный эквивалент цифры
- количественный эквивалент цифры 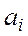 в нулевом разряде. В дальнейшем, там, где это не приведет к недоразумениям, мы будем записи
в нулевом разряде. В дальнейшем, там, где это не приведет к недоразумениям, мы будем записи 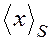 и
и 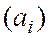 заменять записями
заменять записями 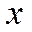 и
и 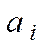 соответственно.
соответственно.
Доказано, что в так называемых канонических системах такого типа (системах, удовлетворяющих требованиям однозначности, конечности и эффективности представления чисел) для записи произвольных количеств достаточно 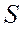 цифр. При этом различают смещенные, симметричные и кососимметричные канонические естественные системы счисления с натуральным основанием.
цифр. При этом различают смещенные, симметричные и кососимметричные канонические естественные системы счисления с натуральным основанием.
В смещенных системах количественные эквиваленты цифр в нулевом разряде либо только положительны (для этого наиболее часто выбираются первые 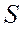 натуральных чисел ряда, включая 0), либо только отрицательны (количественным эквивалентом здесь служат те же величины, взятые с обратным знаком). Это наиболее часто используемые в ЭВМ системы счисления. К ним относятся обычная десятичная, а также двоичная, восьмеричная и др. системы, которые будут рассмотрены ниже.
натуральных чисел ряда, включая 0), либо только отрицательны (количественным эквивалентом здесь служат те же величины, взятые с обратным знаком). Это наиболее часто используемые в ЭВМ системы счисления. К ним относятся обычная десятичная, а также двоичная, восьмеричная и др. системы, которые будут рассмотрены ниже.
Симметричная система счисления имеет нечетное натуральное основание 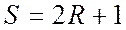 и цифры, количественные эквиваленты которых в нулевом разряде являются элементами множества
и цифры, количественные эквиваленты которых в нулевом разряде являются элементами множества 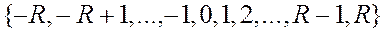 .
.
Эти системы используются реже, хотя по ряду характеристик они явно предпочтительней смещенных систем. Так, к примеру, при одинаковых основаниях и, следовательно, одном и том же числе используемых цифр в симметричной системе счисления могут быть представлены все целые числа, а в смещенной – только числа одного знака. Ниже мы рассмотрим пример симметричной системы счисления с S = 3.
В кососимметричной системе общее число цифр также равно основанию системы, но их количественные эквиваленты в нулевом разряде определяются множеством 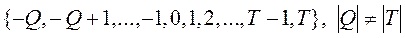 . Ввиду малой эффективности использования таких систем в ЭВМ мы их рассматривать не будем.
. Ввиду малой эффективности использования таких систем в ЭВМ мы их рассматривать не будем.
Легко показать, что с помощью n разрядов, имеющих номера 0,1,…,n-1, в смещенной, симметричной и кососимметричной системах можно представить все целые числа из диапазонов 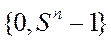 или
или 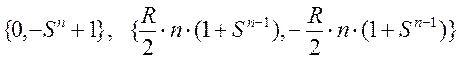 и
и 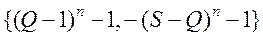 соответственно.
соответственно.
Известны также так называемые избыточные естественные системы с натуральным основанием. В этих системах, удовлетворяющих требованиям конечности и эффективности представления чисел, не удовлетворяется требование однозначности кодирования хотя бы одного числа. С помощью избыточных систем достигается либо упрощение выполнения арифметических операций, либо повышение надежности представления информации в машине. К их числу относятся, к примеру, квазиканонические, а также модифицированные квазиканонические системы счисления [3.1].
Рассмотрим подробнее некоторые наиболее часто используемые в ЭВМ естественные системы счисления.
3.1.3.1. В двоичной системе используются только две цифры 0 и 1. Взятые в отдельности, они обозначают соответствующие цифры натурального ряда. Основание системы 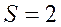 записываются в ней в виде 10. Таблицы сложения и умножения одноразрядных чисел имеют вид (см. табл. (3.1, 3.2).
записываются в ней в виде 10. Таблицы сложения и умножения одноразрядных чисел имеют вид (см. табл. (3.1, 3.2).




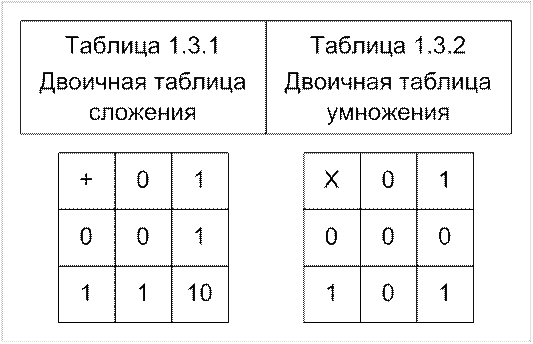
С помощью этих таблиц сложение, вычитание, умножение и деление многоразрядных двоичных чисел производится по тем же правилам, по которым выполняются соответствующие им операции в привычной для нас десятичной системе.
Так, например:
1011011,011 + 10111,111 = 1110011,010;
10110,1101 - 10001,1111 = 100,1110;
1100111 × 11,011 = 101011110,0101111;
11011101101: 1001 = 11000101.
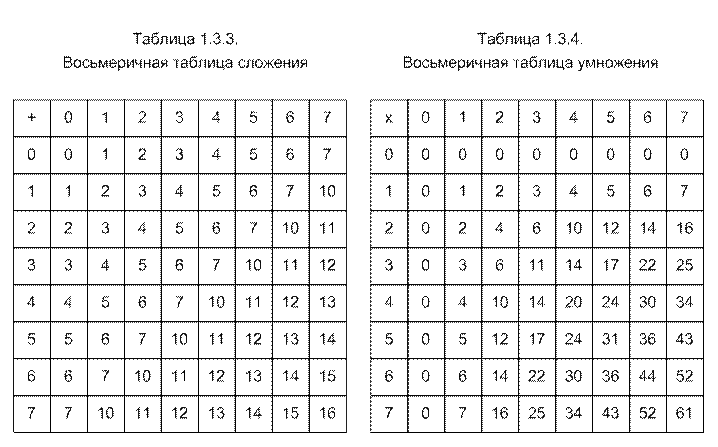
3.1.3.2. Восьмеричная система пользуется цифрами 0,1,2,3,4,5,6,7, которые, будучи взятыми в отдельности, обозначают соответствующие им числа натурального ряда. Основание системы счисления 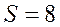 записывается здесь обычным образом. Одноразрядное восьмеричное сложение и умножение выполняются по табл.3.3 и 3.4. Пользуясь ими, легко можно сложить, вычесть, умножить и разделить два произвольных восьмеричных числа.
записывается здесь обычным образом. Одноразрядное восьмеричное сложение и умножение выполняются по табл.3.3 и 3.4. Пользуясь ими, легко можно сложить, вычесть, умножить и разделить два произвольных восьмеричных числа.
Например,
327,71102 + 35, 67735 = 365,61037;
11076,01 – 705,62 = 10170,17;
173,261 × 16,35 = 3366,56615;
336656,615: 1635 = 173,261.


3.1.3.3. В шестнадцатеричной системе общепринятых десятичных цифр уже не хватает для записи чисел. Наиболее часто для этих целей используют цифры 0,1,2,3,4,5,6,7,8,9,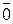 ,
,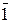 ,
,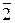 ,
,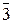 ,
,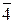 ,
,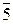 , соответствующие первым шестнадцати числам натурального ряда, включая 0. Таблицы сложения и умножения одноразрядных чисел здесь довольно громоздки. Пользуясь ими, выполняют арифметические действия над многоразрядными числами.
, соответствующие первым шестнадцати числам натурального ряда, включая 0. Таблицы сложения и умножения одноразрядных чисел здесь довольно громоздки. Пользуясь ими, выполняют арифметические действия над многоразрядными числами.
3.1.3.4. Троичная симметричная система использует цифры 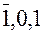 , которым в нулевом разряде соответствуют эквиваленты -1, 0 и 1. Основание здесь, как обычно, имеет вид 10. Знак числа определяется видом первой значащей цифры, отличной от нуля. Таблицы сложения и умножения одноразрядных чисел в этой системе достаточно просты (см. табл. 3.5 и 3.6).
, которым в нулевом разряде соответствуют эквиваленты -1, 0 и 1. Основание здесь, как обычно, имеет вид 10. Знак числа определяется видом первой значащей цифры, отличной от нуля. Таблицы сложения и умножения одноразрядных чисел в этой системе достаточно просты (см. табл. 3.5 и 3.6).


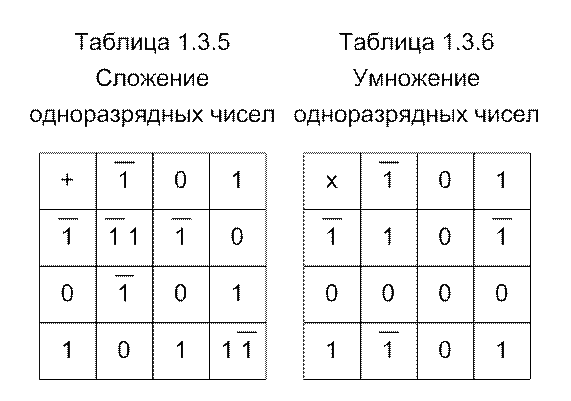
С их помощью легко складываются, вычитаются, умножаются и делятся многоразрядные числа. При этом полезно помнить, что 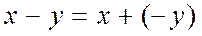 , а
, а 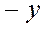 легко находится по
легко находится по 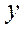 . Действительно, если
. Действительно, если 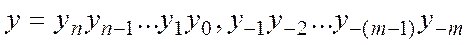 , то
, то
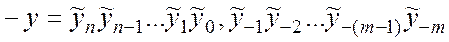 , где
, где
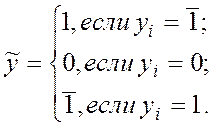
Например:
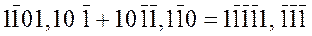 ;
; 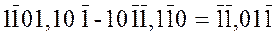 ;
;
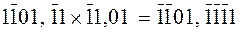 ;
; 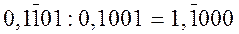 .
.
Как отмечалось, для кодирования чисел в троичной симметричной системе нет необходимости во введении специального символа для обозначения знака, а это ведет к отсутствию в ЭВМ, работающей в этой системе, специального кодирования для производства арифметических операций над числами с произвольными знаками. Ниже будет показано, что из всех естественных систем с натуральным основанием она наиболее экономична по числу цифро-разрядов, необходимых для представления числа в заранее заданном диапазоне. В этой системе функционировала уникальная отечественная ЭВМ «Сетунь».
3.1.3.5. В системах счисления с целым отрицательным основанием 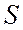 произвольное число
произвольное число 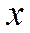 также может быть представлено в виде:
также может быть представлено в виде:
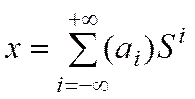 , (3.2)
, (3.2)
где 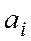 - цифры системы, число которых равно
- цифры системы, число которых равно 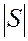 , а их количественные эквиваленты в нулевом разряде
, а их количественные эквиваленты в нулевом разряде 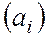 могут определяться, к примеру, множеством
могут определяться, к примеру, множеством 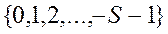 . Причем, если некоторое число в такой системе имеет конечное представление, то оно является единственным. Неединственным образом здесь представляются числа вида
. Причем, если некоторое число в такой системе имеет конечное представление, то оно является единственным. Неединственным образом здесь представляются числа вида
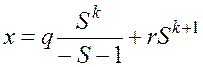 ,
,
где 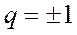 , а
, а 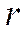 и
и 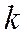 - любые целые числа. Каждое из таких чисел имеет два различных бесконечных представления вида (3.2).
- любые целые числа. Каждое из таких чисел имеет два различных бесконечных представления вида (3.2).
Рассмотрим этот класс систем на примере системы с основанием 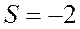 .
.
В минус двоичной системе используемые цифры, их количественные эквиваленты, вид основания, таблица умножения одноразрядных чисел – те же, что и в обычной двоичной системе. Таблица сложения приведена ниже (табл.3.7).

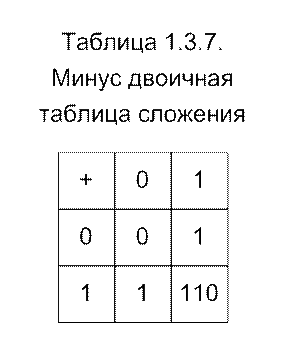
Так же, как и в троичной симметричной системе, здесь нет необходимости во введении специального символа для обозначения знака числа. О его знаке судят по номеру старшего значащего разряда (при четном по модулю номере число положительно, при нечетном - отрицательно).
Непосредственное сложение многоразрядных чисел с помощью приведенной выше таблицы приводит к необходимости учета в общем случае нескольких единиц переноса в i-й разряд. Причем процедура сложения может продолжаться бесконечно. Для ее упрощения можно принять, что единица i-го разряда «уничтожается» двумя единицами (i-1)-го разряда. Действительно,
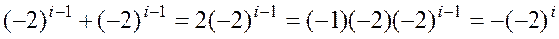 .
.
Вычитание многоразрядных чисел здесь, как и в случае троичной симметричной системы, легко сводится к сложению, так как 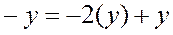 , т.е. вычитание
, т.е. вычитание 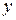 можно заменить его прибавлением с последующим добавлением к полученному результату вычитаемого, сдвинутого на один разряд влево. Последнее соотношение можно рассматривать как правило получения в минус двоичной системе кода отрицательного числа.
можно заменить его прибавлением с последующим добавлением к полученному результату вычитаемого, сдвинутого на один разряд влево. Последнее соотношение можно рассматривать как правило получения в минус двоичной системе кода отрицательного числа.
Единственным отличием умножения многоразрядных чисел в системе с основанием S = -2 от их умножения в обычной двоичной системе является то, что частичные произведения здесь суммируются с использованием табл.3.7.
Правила деления имеют существенные отличия и рассматриваться не будут.
Приведем примеры выполнения арифметических операций в минус двоичной системе:
1,1010010 + 0,1101001 = 0,0111011;
1,1101 – 0,0110 = 1,1111;
0,1101 х 1,0010 = 0,0010;
11001: 111 = 111.
В заключение отметим, что достоинства этой системы очевидны, а недостатки связаны, в основном, с неоднозначностью записи отдельных чисел, несимметричностью их представления при заранее фиксированном количестве разрядов и др.
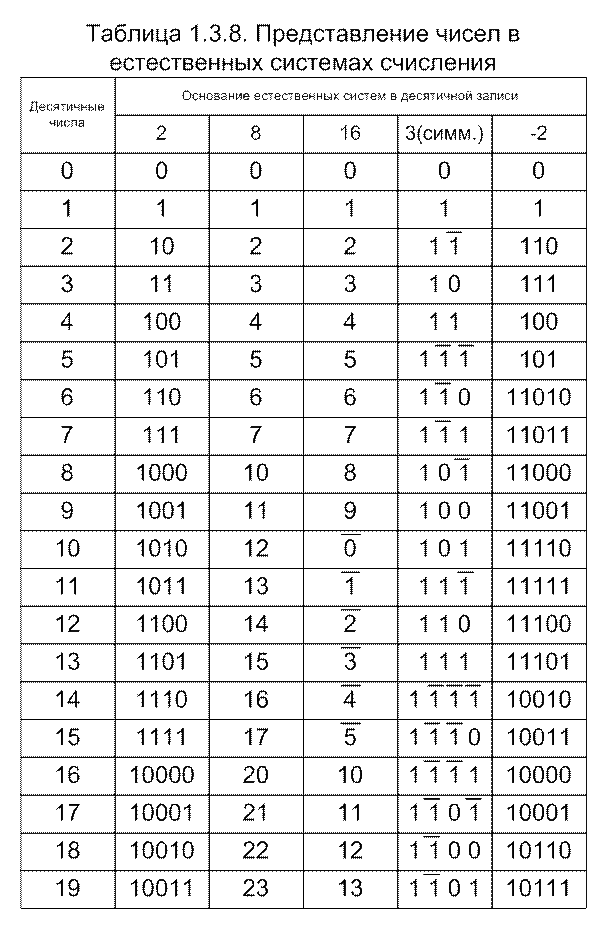
Приведем таблицу записи десятичных чисел от 0 до 20 в рассмотренных естественных системах:

|
Дата добавления: 2014-01-20; Просмотров: 2614; Нарушение авторских прав?; Мы поможем в написании вашей работы!