Сравнение различных систем счисления с точки зрения их применения в ЭВМ

Системы счисления в остаточных классах

Рассмотрим множество всех натуральных чисел N, включая 0. Выберем далее n целых взаимно простых положительных чисел и для каждого числа найдем наименьшие положительные остатки от его деления на соответственно. Ясно, что число различных совокупностей остатков будет равно . При этом все множество 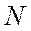может быть разбито на 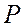непересекающихся классов, в каждый из которых входят все числа из , имеющие одинаковые совокупности остатков. Эти классы называются остаточными классами. Каждому из них можно присвоить код, равный соответствующему ему набору остатков.

Если же все или некоторые из не будут взаимно простыми числами, то , т.к. появление отдельных совокупностей остатков становится невозможным. Действительно, остаток по некоторому числу 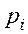в этом случае уже предопределяет остаток по числу , не являющемуся взаимно простым с . Так, к примеру, при появление наборов остатков (0,1), (0,3), (1,2), и (1,0) невозможно.

Предположим теперь, что выбрана некоторая система взаимно простых чисел и произвольное число . Ему может быть однозначно поставлен в соответствие код некоторого остаточного класса, к которому оно принадлежит. Обратного, к сожалению, сделать нельзя, т.е. невозможно назвать по коду класса число , о котором идет речь, поскольку каждый класс состоит из бесконечного множества элементов.

Для обеспечения взаимной однозначности выделим в каждом классе элемент, минимальный по своему числовому значению. Назовем его главным элементом класса. Обозначим символом множество главных элементов всех классов для данных 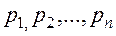. Если теперь рассматривать только множество 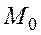, то при фиксированной системе между каждым числом и кодом класса существует взаимно однозначное соответствие. Вместо множества можно брать любое множество , элементы которого получаются из элементов прибавлением к каждому из них числа 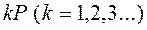. Ясно также, что мощность множества зависит от того, какая система чисел используется. При этом, как уже отмечалось, желательно выбрать эти числа взаимно простыми. Тогда включает в себя элементов .

Системой счисления в остаточных классах (ССОК) называется такая система, в которой целое положительное число 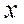представляется в виде набора наименьших положительных остатков , получаемых от деления на каждое из целых положительных взаимно простых чисел , называемых основаниями (модулями) системы. При этом предполагается, что , где может быть одним из чисел натурального ряда, включая 0. Здесь по–прежнему . Следует заметить, что ССОК не является весомозначной.

Таким образом, . Величины называют еще цифрами системы и обозначают , i=1,2, …,n, поскольку где – целая часть числа , а диапазон чисел, представимых в ССОК, изображают в виде так называемого модульного кольца (рис. 3.1). Он может быть также охарактеризован для наиболее часто используемых модулей табл. 3.10. Третий и четвертый ее столбцы дают количество двоичных разрядов, необходимых для записи в ССОК с использованием двоичной системы любой цифры 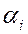i-го разряда и любого числа из диапазона Р представимых чисел соответственно.

Рис. 3.1. Модульное кольцо

3.10

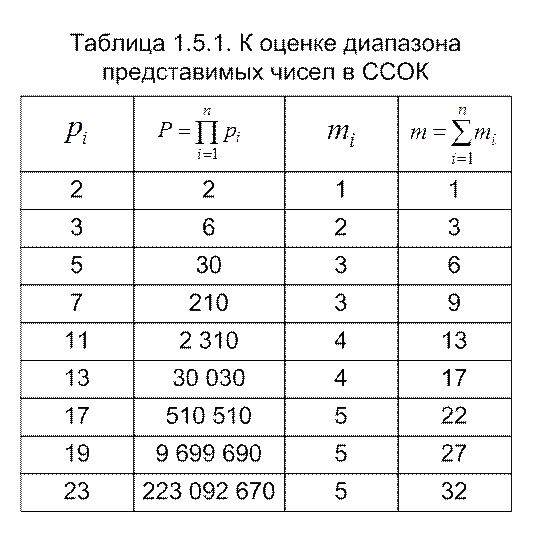
Рассмотрим правила выполнения в ССОК операций сложения и умножения над целыми положительными числами.

Пусть , ,

,

и .

Покажем, что , (3.4)

, (3.5)

т.е. и есть наименьшие положительные остатки от деления на и соответственно ().

Действительно,

, . (3.6)

Можно также записать, что , , 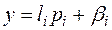где - некоторые целые неотрицательные числа.

Тогда ,

;

,

.

Подставляя эти соотношения в (3.6), нетрудно получить выражения (3.4) и (3.5).

Так, например, если и x=17=(2,2,3), y=6=(0,1,6), то x+y=(2,3,2), xy=(0,2,4). Легко проверяется, что числа (2,3,2) и (0,2,4) есть 23 и 102, равные x+y и xy соответственно.

Можно также показать, что разность чисел и при можно вычислить на базе соотношения

причем, если разность цифр , то следует взять её дополнение к основанию 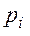. Однако деление чисел в ССОК вызывает большие трудности. Пока что нет алгоритмов деления, позволяющих реализовать его за малое время при небольших затратах оборудования. Предлагаемые для этих целей методы деления с помощью специально вычисляемой двоичной функции, аппроксимирующей частное, мы рассматривать не будем.

К достоинствам ССОК следует отнести:

- независимость получения цифр числа, что позволяет при выполнении арифметических операций обрабатывать разряды параллельно без учета межразрядных связей;

- малоразрядность остатков при записи их в какой-либо позиционной системе, что открывает возможность построения табличной арифметики, т.е. простого выбора результатов большинства операций из заранее составляемых таблиц.

Недостатками этой системы являются:

- невозможность визуального сопоставления чисел;

- отсутствие простых признаков выхода результата за пределы диапазона [0,P);

- ограниченность сферой целых положительных чисел;

- сложность выполнения операции деления;

- трудности, связанные с приближенным выполнением операций, округлением результата и другие.

Некоторые пути преодоления этих недостатков изложены в разделе 2.

Введенные ниже оценки эффективности использования в ЭВМ различных систем счисления применимы, в основном, к естественным системам с натуральным основанием. Они далеко не охватывают всех аспектов, связанных с упомянутой эффективностью, поскольку относятся лишь к представлению информации в ЭВМ и производству в ней отдельных арифметических операций. Следует помнить также, что эти оценки несут сугубо приближенный характер и сильно зависят от выбранной элементной базы, алгоритмической и схемной реализации соответствующих вычислительных процедур.

Оценим прежде всего количество оборудования, необходимого для представления в ЭВМ чисел в различных системах счисления. Пусть 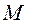- число этих чисел (при представлении целых положительных чисел под можно понимать максимальное представимое число). Тогда для их записи в системе с основанием потребуется разрядов, где

Интуитивно чувствуется, что сложность представления чисел в ЭВМ можно охарактеризовать величиной . Действительно, для представления произвольной цифры в заранее заданном разряде необходимо тем больше единиц оборудования, чем больше S. Правда, прямая пропорциональность между числом единиц оборудования, затрачиваемых на один разряд, и значением S на практике отсутствует, но для грубой оценки можно предположить, что это имеет место. Тогда величина 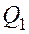характеризует общие затраты оборудования в рассматриваемом случае.

Для исключения произвольной величины введем относительную функцию затраты оборудования

. (3.7)

При соотношение (3.7) можно переписать в виде

.

Легко показать, что 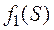имеет минимум при S=e. Её значения для некоторых целых S приведены в табл. 3.11.

3.11

Как видим, наименьшие затраты оборудования имеют место при S=3. Относительно небольшие потери по сравнению с оптимальным случаем получаются при использовании оснований 2 и 4. При основании же S=10 затраты оборудования на 50% больше, чем при S=2.

В формуле предполагается, что для представления информации в одном разряде требуется S единиц оборудования. Практически для этих целей наиболее часто используется двухпозиционных элементов и двоичное неизбыточное кодирование цифр. Тогда число таких элементов для представления различных чисел

а соответствующая относительная оценка

.

Значения приведены в табл. 3.11. Как видим, наибольшую экономию в числе двухпозиционных элементов дают системы с основаниями 2,4,8. При S=10 затраты элементов только на 20% больше, чем при S=2. Если , то , что свидетельствует о целесообразности использования для целей представления информации систем с большими основаниями при двоичном кодировании их цифр. Легко заметить, что при S>6 . Следовательно, в этом случае выгоднее применять двухпозиционные элементы, чем S-позиционные, если последние в S/2 раз сложнее первых.

Интересно также оценить влияние значения S на время выполнения арифметических операций сложения и умножения (вычитание по затратам времени эквивалентно сложению, деление же в ЭВМ используется довольно редко). Однако при оценке влияния величины S на время сложения чисел в ЭВМ пришлось бы затронуть структурные схемотехнические вопросы, что преждевременно. То же справедливо и для операции умножения, поскольку умножение в машинах сводится к последовательности сдвигов и сложений кодов чисел, участвующих в операции. Тем не менее, для одного частного случая суммирования чисел, когда время выполнения последнего не зависит от S, и наиболее распространенного алгоритма умножения такую оценку получить можно.

Предположим, что реализуется следующий алгоритм умножения: при анализе очередного разряда множителя множимое прибавляется к содержимому сумматора столько раз, какова цифра множителя; далее содержимое сумматора сдвигается на один разряд вправо, анализируется следующий старший разряд множителя, и процедура повторяется.

Если положить, что появление в каждом разряде множителя любой цифры от 0 до S-1 равновероятно, то среднее число сложений при умножении на один разряд множителя равно (S-1)/2, общее число сложений, необходимых для перемножения двух чисел в системе с основанием S при фиксированном М,

а соответствующая относительная оценка

. (3.8)

Величина показывает, во сколько раз количество сложений в системе с основанием S в среднем больше, чем в системе с основанием 2. Если далее принять, что время сдвига равно 0, а время сложения не зависит от S, то соотношение (3.8) характеризует относительные затраты времени на умножение. Значения приведены в таблице 3.11. Как видно из таблицы, для рассматриваемого алгоритма умножения при S=2 затраты времени минимальны.

Выполнение операции умножения в ЭВМ можно ускорить, если анализировать несколько разрядов множителя одновременно. Специальные исследования показали, что при этом предпочтение следует отдать канонической двоичной системе счисления.

Все вышеизложенное не позволяет, конечно, раз и навсегда определить систему, наиболее целесообразную для использования в ЭВМ. Применение отдельных систем (например, симметричной троичной) тормозит элементная база, в других случаях (системы счисления в остаточных классах) не закончено решение алгоритмических и структурных вопросов. Кроме того, сколько-нибудь исчерпывающий перечень требований, которым должна отвечать система счисления при ее использовании в ЭВМ настолько велик, что выполнить их все одновременно просто невозможно. Так, к примеру, сторонники единой мировой системы счисления выдвинули идею о переходе при всех измерениях и расчетах на систему счисления с основанием 12, так как основание 12 имеет наибольшее число различных делителей по сравнению с другими небольшими по величине основаниями, близкими к 10, и следовательно, в этой системе будет записываться в конечном виде большее число дробей. Исследования в этом направлении будут продолжаться.

В настоящее время во всех ЭВМ используется двоичная система счисления. При этом в качестве служебных используются, как правило, восьмеричная, десятичная, шестнадцатеричная и двоично-десятичная системы. Все рассмотренные выше оценочные функции дают для неё хорошие результаты. Следует отметить также простоту выполнения в этой системе всех арифметических и логических операций, возможность широкого применения для анализа и синтеза двоичных схем хорошо разработанного аппарата математической логики, развитую двоичную элементную базу, отличающуюся высоким быстродействием и надежностью. Вместе с тем следует отметить, что в машинах, имеющих невысокую производительность, частый ввод и вывод данных и ориентированных на решение бухгалтерских, экономических, информационных и других задач, часто применяется восьмеричная или десятичная система счисления. Известны ЭВМ, в которых двоичная и двоично-десятичная системы используются в качестве основных систем одновременно, а также существуют ЭВМ, работающие в троичной симметричной, минус двоичной, ССОК и других системах.

Дата добавления: 2014-01-20