Показательный (экспоненциальный) закон распределения

Определение 2. Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром 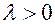, если ее плотность вероятности имеет вид:

(8)

Функция распределения случайной величины, распределенной по показательному закону, равна

(9)

Действительно,

при , ,

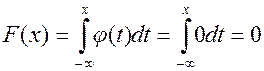при , .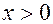

Кривая распределения 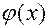и график функции распределения приведены ниже:

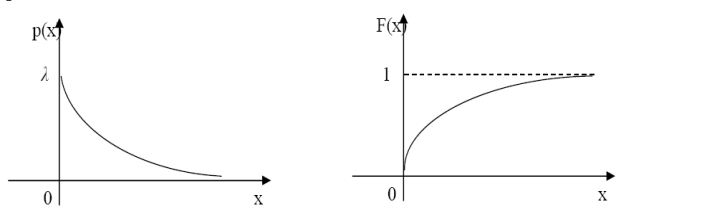
Для случайной величины, распределенной по показательному закону

(10)

Действительно,

=

.

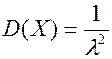, (11)

Вероятность попадания в интервал 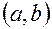непрерывной случайной величины Х, распределенной по показательному закону, находится по формуле

(12)

Замечание 1. Показательный закон распределения вероятностей встречается во многих задачах, связанных с простейшим потоком событий. Под потоком событий понимают последовательность событий, наступающих одно за другим в случайные моменты. Например, поток вызовов на телефонной станции, поток заявок в системе массового обслуживания и др.

Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого

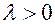, () (13)

определяет вероятность отказа элемента за время длительностью t. Здесь Т – длительность времени безотказной работы элемента, λ − интенсивность отказов (среднее число отказов в единицу времени).

Функция надежности

(14)

определяет вероятность безотказной работы элемента за время длительностью t.

Пример 2. Установлено, что время ремонта магнитофонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт магнитофона потребуется не менее 15 дней, если среднее время ремонта магнитофонов составляет 12 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины Х.

Решение. По условию математическое ожидание =12, откуда параметр и тогда плотность вероятности и функция распределения имеют вид: , (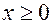). Искомую вероятность 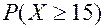можно найти, используя функцию распределения:

.

Среднее квадратическое отклонение 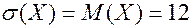дней.

Пример 3. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону:

для первого элемента ;

для второго ;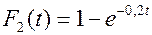

для третьего элемента .

Найти вероятности того, что в интервале времени (0;5) ч. откажут: а) только один элемент; б) только два элемента; в) все три элемента.

Решение. Вероятность отказа первого элемента

.

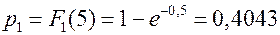Вероятность отказа второго элемента

.

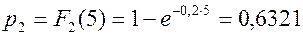Вероятность отказа третьего элемента

.

Искомая вероятность

а) .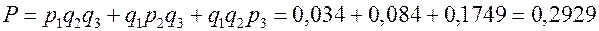

б) .

в) .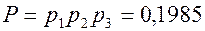

3. Нормальное распределение. В теории вероятностей и математической статистике важнейшую роль играет так называемое нормальное или гауссовское распределение. Оно также широко применяется и при решении прикладных задач. Значимость нормального распределения определяется тем, что оно служит хорошим приближением для большого числа наборов случайных величин, получаемых при наблюдениях и экспериментах. Нормальное распределение почти всегда имеет место, когда наблюдаемые случайные величины формируются под влиянием большого числа случайных факторов, ни один из которых существенно не превосходит остальные.

Определение 3. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и σ, если ее плотность вероятности имеет вид:

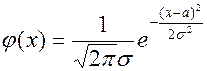, (15)

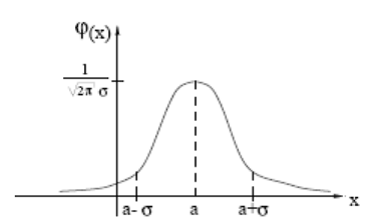
Кривую нормального закона распределения называют нормальной или кривой Гаусса.

График функции плотности нормального закона представляет собой колоколообразную кривую, принимающую наибольшее значение в точке и быстро убывающую при .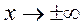

Докажем, что 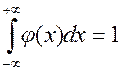. Действительно

.

Используя несобственные двойные интегралы можно доказать, что

. (16)

Этот интеграл называется интегралом Пуассона. Подставив этот результат в последнее выражение, получим .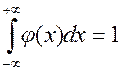

Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, и вероятности ее попадания на некоторый промежуток связана с тем, что интеграл от функции (15) не берется в элементарных функциях. Поэтому ее выражают через функцию Лапласа (интеграл вероятностей), для которой составлены таблицы.

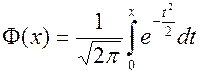(17)

Найдем функцию распределения случайной величины Х, распределенной по нормальному закону:

.

Так как 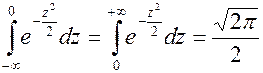(подынтегральная функция четная).

Таким образом,

(18)

Для случайной величины, распределенной по нормальному закону,

, (19)

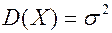. (20)

Выясним как будет меняться нормальная кривая при изменении параметров a иσ. Если и меняется параметр a – центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы.

Если 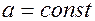и меняется параметр – разброс значений случайной величины от центра симметрии распределения, то при увеличении уменьшается, но т.к. площадь под любой кривой распределения должна оставаться равной 1, то кривая становится более плоской, растягиваясь вдоль оси Ox. При уменьшении увеличивается и нормальная кривая вытягивается вверх, одновременно сжимаясь с боков.

В соответствии со свойством функции распределения, вероятность попадания значений нормальной случайной величины Х в интервал определяется формулой

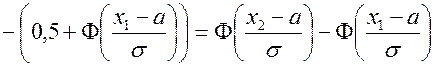. (21)

4. Вероятность заданного отклонения для нормального распределения. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину (по абсолютной величине), равна

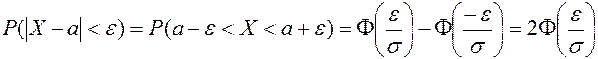. (22)

«Правило трех сигм»: Если случайная величина Х имеет нормальный закон распределения с параметрами а и , т.е. 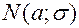, то практически достоверно, что ее значения заключены в интервале :

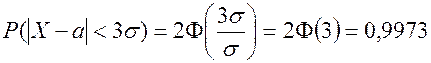(23)

Отклонение по абсолютной величине нормально распределенной СВ X больше, чем на 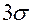, является событием практически невозможным, т.к. его вероятность весьма мала:

Т.к. кривая Гаусса симметрична относительно математического ожидания, то коэффициент асимметрии нормального распределения . Эксцесс нормального распределения Е =0 и крутость других распределений определяется по отношению к нормальному.

Замечание 2. Случайная величина, имеющая нормальное распределения с параметрам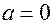и и 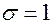, называется стандартной (нормированной) нормальной случайной величиной, а ее распределение – стандартным (нормированным) нормальным распределением.

Плотность и функция стандартного нормального распределения даются формулами:

, .

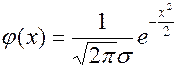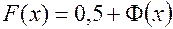Пример 4. Определить закон распределения случайной величины Х, если ее плотность распределения вероятностей задана функцией:

.

Найти математическое ожидание, дисперсию и функцию распределения случайной величины Х.

Решение. Сравнивая данную функцию 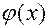с функцией плотности вероятности для случайной величины, распределенной по нормальному закону, заключаем, что случайная величина Х распределена по нормальному закону с параметрами а = 1 и .

Тогда, 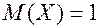, , . Функция распределения случайной величины Х имеет вид:

.

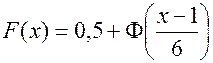Пример 5. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден.ед. и средним квадратическим отклонением 0,2 ден. ед. Найти вероятность того, что цена акции: а) не выше 15,3 ден. ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед. Найти границы, в которых будет находиться текущая цена акции.

Решение. Так как а = 15 и 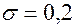, то

а) ,

б) ,

в)

.

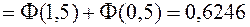По правилу трех сигм и, следовательно, . Окончательно имеем

.

Пример 6. Автомат изготавливает детали, контролируя их диаметры Х. Считая, что случайная величина Х распределена нормально с параметрами мм и 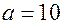мм, найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных деталей.

Решение. Найдем отклонение по известным вероятности отклонения и среднему квадратическому отклонению (по формуле (22)):

.

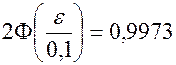По таблице значений функции Лапласа находим, что 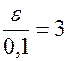. Следовательно, .

Из неравенства получаем или .

Пример 7. Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Пусть математическое ожидание ее равно 175 см, а среднее квадратическое отклонение – 6 см. Определить вероятность того, что хотя бы один из наудачу выбранных пяти мужчин будет иметь рост от 170 до 180 см.

Решение. Найдем вероятность того, что рост мужчины будет принадлежать интервалу (180;170):

.

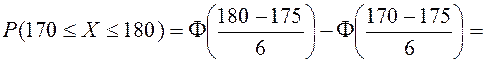
Тогда вероятность того, что рост мужчины не будет принадлежать интервалу (170; 180): . Вероятность того, что хотя бы один из 5 мужчин будет иметь рост от 170 до 180 см равна: .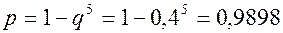

Дата добавления: 2014-01-20