Трендовые модели на основе кривых роста

ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ

МОДЕЛИ ПРОГНОЗИРОВАНИЯ

Основная цель создания трендовых моделей экономической динамики – на их основе сделать прогноз о развитии изучаемого процесса на предстоящий промежуток времени. Прогнозирование на основе временного ряда экономических показателей относится к одномерным методам прогнозирования, базирующимся на экстраполяции, то есть на продлении на будущее тенденции, наблюдавшейся в прошлом.

Предполагается: прогнозируемый показатель формируется под воздействием большого количества факторов, выделить которые либо невозможно, либо по которым отсутствует информация.

Использование метода экстраполяции на основе кривых роста для прогнозирования базируется на двух предположениях:

1. временной ряд экономического показателя действительно имеет тренд, то есть преобладающую тенденцию;

2. общие условия, определявшие развитие показателя в прошлом, останутся без существенных изменений в течение периода упреждения.

Наиболее часто в экономике используются полиномиальные, экспоненциальные и S-образные кривые роста.

Простейшие полиномиальные кривые роста имеют вид:

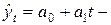полином первой степени;

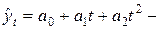полином второй степени;

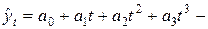полином третьей степени;

и так далее.

Параметр 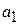называют линейным приростом, а параметр 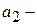ускорением роста, параметр 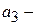изменение ускорения роста.

Для полинома первой степени характерен постоянный закон роста. Если рассчитать первые приросты по формуле

,

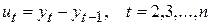то они будут постоянной величиной и равны 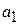. Если первые приросты рассчитать для полинома второй степени, то они будут иметь линейную зависимость от времени и ряд из первых приростов 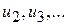на графике будет представлен прямой линией. Вторые приросты: 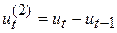для полинома второй степени будут постоянны.

Для полинома третьей степени первые приросты будут полиномами второй степени, вторые приросты – линейными функциями времени, а третьи приросты, рассчитываемые по формуле 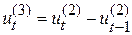, будут постоянными величинами.

На основе сказанного можно отметить следующие свойства полиномиальных кривых роста:

1. от полинома высокого порядка можно путем расчета последовательных разностей (приростов) перейти к полиному более низкого порядка;

2. значения приростов для полиномов любого порядка не зависят от значений самой функции .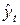

Полиномиальные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня.

Использование экспоненциальных кривых роста предполагает, что дальнейшее развитие зависит от достигнутого уровня, например, прирост зависит от значения функции. В экономике чаще всего применяются две разновидности экспоненциальных (показательных) кривых: простая экспонента и модифицированная экспонента.

Простая экспонента:

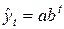, (1)

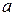где и 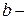положительные числа, при этом, если 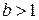, то функция возрастает с ростом времени 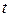, в противном случае – убывает.

Ордината данной функции изменяется с постоянным темпом прироста:

.

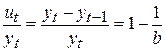Логарифмы ординат простой экспоненты линейно зависят от времени:

.

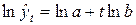Модифицированная экспонента:

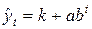, (2)

где постоянные величины: 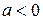, , 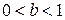а постоянная 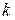носит название асимптоты этой функции, то есть значения функции неограниченно приближаются (снизу) к величине .

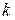Если прологарифмировать первые приросты данной функции, то получится функция, линейно зависящая от времени, при этом:

.

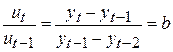В экономике достаточно распространены процессы, которые сначала растут медленно, затем ускоряются, а затем вновь замедляют свой рост, стремясь к какому-либо пределу, например, процесс ввода некоторого объекта в промышленную эксплуатацию. Для моделирования таких процессов используются так называемые S- образные кривые роста, среди которых выделяют кривую Гомперца и логистическую кривую.

Кривая Гомперца:

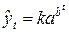, (3)

где 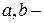положительные параметры, причем 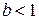; параметр 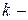асимптота функции.

В кривой Гомперца выделяют четыре участка: на первом – прирост функции незначительный; на втором – прирост увеличивается; на третьем – прирост примерно постоянный; на четвертом – происходит замедление темпов прироста и функция неограниченно приближается к значению .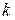

Логарифм данной функции является экспоненциальной кривой; логарифм отношения первого прироста к самой ординате функции – линейная функция времени.

На основе кривой Гомперца описывается, например, динамика показателей уровня жизни, модификация этой кривой используется в демографии для моделирования показателей смертности и т.п.

Логистическая кривая (кривая Перла-Рида):

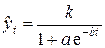; (4)

другой вид этой кривой:

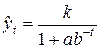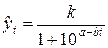; (5)

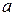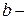В этих выражениях и положительные параметры; 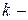предельное значение функции при бесконечном возрастания времени.

Конфигурация графика логистической кривой близка графику кривой Гомперца, но в отличие от последней логистическая кривая имеет точку симметрии, совпадающую с точкой перегиба.

Дата добавления: 2014-01-20