
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частотный критерий Михайлова
|
|
|
|
Критерий Михайлова – это частотный критерий, позволяющий судить об устойчивости замкнутой системы по поведению ее характеристического вектора на комплексной плоскости. Характеристический вектор получают путем подстановки в выражение для характеристического полинома
 ,
,
Значения  . Тогда характеристический вектор представляется комплексной величиной, определяемой как:
. Тогда характеристический вектор представляется комплексной величиной, определяемой как:
 ,
,
где

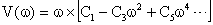
Если задаваться различными значениями  и откладывать значения
и откладывать значения 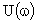 по горизонтальной, а
по горизонтальной, а  – по вертикальной осям декартовой системы координат, то будет получена кривая, называемая годографом характеристического вектора или годографом Михайлова. Другая формулировка: годографом Михайлова называется множество точек, образованных при движении характеристического вектора САУ при изменении частоты от 0 до
– по вертикальной осям декартовой системы координат, то будет получена кривая, называемая годографом характеристического вектора или годографом Михайлова. Другая формулировка: годографом Михайлова называется множество точек, образованных при движении характеристического вектора САУ при изменении частоты от 0 до  .
.
То есть для устойчивости САУ необходимо выполнение условия вида:
 .
.
Для вывода этого утверждения представим характеристический полином в виде
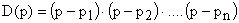 ,
,
где 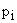 – корни характеристического уравнения
– корни характеристического уравнения  .
.
На комплексной плоскости каждому корню соответствует определенная точка. Подставив  , получаем
, получаем
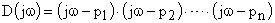 .
.
Каждый вектор 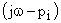 может быть представлен в виде вектора, начало которого лежит в точке, определяющей корень
может быть представлен в виде вектора, начало которого лежит в точке, определяющей корень 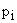 а конец лежит на мнимой оси. Следовательно,
а конец лежит на мнимой оси. Следовательно, 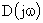 можно представить суммарным вектором, равным произведению элементарных векторов. Модуль суммарного вектора будет равен произведению модулей отдельных векторов, а фаза – сумме фаз этих векторов. При изменении частоты конец каждого вектора будет перемещаться вдоль мнимой оси. При изменении частоты от
можно представить суммарным вектором, равным произведению элементарных векторов. Модуль суммарного вектора будет равен произведению модулей отдельных векторов, а фаза – сумме фаз этих векторов. При изменении частоты конец каждого вектора будет перемещаться вдоль мнимой оси. При изменении частоты от 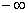 до
до  каждый составляющий вектор, начало которого лежит на вещественной оси, повернется на угол, равный
каждый составляющий вектор, начало которого лежит на вещественной оси, повернется на угол, равный  , если его начало лежит в левой полуплоскости, и равный –
, если его начало лежит в левой полуплоскости, и равный –  , если его начало лежит в правой полуплоскости. Каждая пара комплексно-сопряженных корней – соответственно на угол +
, если его начало лежит в правой полуплоскости. Каждая пара комплексно-сопряженных корней – соответственно на угол + .
.
|
|
|
Если характеристическое уравнение имеет m корней в правой полуплоскости, то в левой полуплоскости число этих корней будет равно n-m. При изменении частоты от 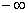 до
до  суммарный угол поворота вектора характеристического полинома определяется как
суммарный угол поворота вектора характеристического полинома определяется как
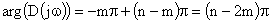 .
.
Для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой полуплоскости, то есть чтобы  . Таким образом, если вектор характеристического полинома замкнутой САУ порядка "n" при изменении частоты от
. Таким образом, если вектор характеристического полинома замкнутой САУ порядка "n" при изменении частоты от 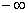 до
до  описывает в положительном направлении угол n
описывает в положительном направлении угол n , то такая система регулирования будет устойчива. В противном случае САУ будет неустойчива.
, то такая система регулирования будет устойчива. В противном случае САУ будет неустойчива.
В силу симметричности кривой, описываемой концом вектора характеристического полинома, можно ограничиться рассмотрением лишь ее части, соответствующей положительным значениям частоты. При этом угол, описываемый вектором характеристического полинома при изменении частоты от 0 до  , уменьшится вдвое и будет определяться как
, уменьшится вдвое и будет определяться как
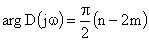 .
.
Формулировка критерия: для устойчивости системы необходимо и достаточно, чтобы ее характеристический вектор при изменении частоты от 0 до  повернулся в положительном направлении (против часовой стрелки), начиная с положительной вещественной оси на число квадрантов, равное порядку характеристического уравнения.
повернулся в положительном направлении (против часовой стрелки), начиная с положительной вещественной оси на число квадрантов, равное порядку характеристического уравнения.
На рис. 3 приведены годографы Михайлова для устойчивых и неустойчивых САУ. Изменение коэффициента 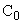 вызывает сдвиг годографа Михайлова вдоль горизонтальной оси без его деформации. Это дает возможность оценить предельное значение этого коэффициента, при котором сохраняются условия устойчивой работы САУ.
вызывает сдвиг годографа Михайлова вдоль горизонтальной оси без его деформации. Это дает возможность оценить предельное значение этого коэффициента, при котором сохраняются условия устойчивой работы САУ.

Рис. 3. Годографы Михайлова для устойчивых и неустойчивых САУ
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 636; Нарушение авторских прав?; Мы поможем в написании вашей работы!