Гармонический осциллятор. Теперь рассмотрим обобщенную задачу о гармоническом осцилляторе, т.е

Теперь рассмотрим обобщенную задачу о гармоническом осцилляторе, т.е. о какой-либо системе, совершающей колебания, описываемые уравнением вида (9.6) или (9.14):

. (9.18)

Примерами гармонического осциллятора являются пружинный, физический и математический маятники, электрический колебательный контур без потерь и т.п. системы без потерь энергии.

1. Пружинный маятник: В простейшем случае пружинный маятник представляет собой груз (материальную точку) массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = ─kх, где k – жесткость пружины.

Естественно, что уравнение движения такого маятника будет описываться уравнением (9.14):

, или . (9.19)

Из уравнений (9.18) и (9.1) следует, что груз, подвешенный на пружине, т.е. физический маятник, совершает гармонические колебания по закону х (t) =

= А соs (ω_о t + φ) с циклической частотой ω₀, равной

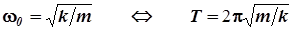. (9.20)

Формула (9.20) справедлива для упругих колебаний груза на пружине, т.е. при деформации пружины в пределах, когда выполняется закон Гука, т.е. когда масса пружины мала по сравнению с массой тела, а груз не вызывает необратимой деформации пружины.

Максимальная потенциальная энергия пружинного маятника (а также полная энергия системы) может быть найдена по формуле:

(9.21)

Математический маятник:

Математический маятник – это идеализированная система, состоящая из материальной точки массой m, подвешенной на невесомой нерастяжимой нити (стержне) длиной l, и колеблющаяся под действием силы тяжести (см. рис. 9.3).

Рис. 9.3. К выводу формулы для периода колебаний математического маятника: точка О – положение равновесия; ВО=ВС= l – длина невесомой нити (подвеса); точка В – точка подвеса

Отклоним шарик (материальную точку) на малый угол φ и отпустим – под действием составляющей силы тяжести Fв (возвращающая сила) материальная точка будет совершать колебания.

Покажем, что при малых углах отклонения эти колебания будут гармоническими и найдём период этих колебаний.

Разложим мысленно силу тяжести , действующую на материальную точку в положении С на две составляющие , направленные соответственно вдоль стержня и перпендикулярно к нему. Сила = m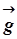Cos α будет растягивать стержень у уравновесится силой реакции стержня 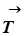. Неуравновешенной останется составляющая силы тяжести . Когда груз придет в наинизшее положение, т.е. в точку О, силы и полностью уравновесятся, т.е. точка О есть положение равновесия материальной точки.

При колебаниях материальная точка будет двигаться по дуге окружности ОС, но для малых углов с большой степенью точности можно заменить дугу ОС хордой ОС, которая в точке С будет эквивалентна касательной к дуге окружности ОС в точке С. Поэтому условно можно будет считать что материальная точка совершает колебания вдоль прямой на которой находится хорда ОС. Совместим ось оХ с хордой ОС, поместив начало координат в точу О и запишем 2-й закон Ньютона для движения точки:

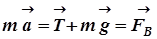
(9.22)

Для малых углов справедливы соотношения:

, (9.23)

поэтому уравнение (9.22) в проекции на ось оХ запишется в виде:

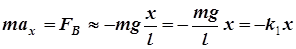. (9.24)

Сравнивая уравнение (9.24) с уравнением (9.14), видим, что возвращающая сила F_B является квазиупругой силой с коэффициентом k₁ = mg / l. Но для уравнения (9.14) мы уже знаем решение:

, (9.25)

так что для математического маятника:

. (9.26)

Амплитуда колебаний А и начальная фаза колебаний φ₀ математического маятника будут зависеть от начального смещения материальной точки от положения равновесия и от её начальной скорости в момент времени t=0. Формула (9.26) для периода колебаний математического маятника при малых углах отклонения от положения равновесия носит название формулы Гюйгенса.

3. Физический маятник:

Это твёрдое (материальное) тело, которое может совершать гармонические колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, расположенной выше центра масс маятника (см. рис. 9.4).

Рис. 9.4. К выводу формулы для периода колебаний физического маятника:

точка О – горизонтальная ось вращения; точка С – центр масс физического маятника.

Отклоним физический маятник (например, в виде однородного стержня массой m и длиной l, точка подвеса которого находится на одном из концов, как это изображено на рис. 9.4.) на малый угол φ – в этом положении маятника у силы тяжести появится плечо ОD = а. Поэтому мы можем записать основное уравнение динамики вращательного движения:

. (9.27)

Если обозначить ОС = d – расстояние от оси вращения до центра масс физического маятника, то a = d sin φ ≈ dφ при малых углах φ. Тогда уравнение (9.27) перепишется в виде:

, (9.28 а)

или

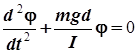(9.28 б)

(отсчёты угла φ и возвращающей силы Fв всегда направлены противоположно, отсюда и знак «─» в уравнении). Но уравнение (9.28б) нам уже известно – это и уравнение (9.14) и уравнение (9.19), так что мы можем сразу записать соотношения:

. (9.29)

По аналогии с пружинным маятником:

. (9.30)

Иногда формулу (9.29) записывают в форме, которую мы получили для математического маятника:

, (9.31)

где ─ приведенная длина физического маятника.

Если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников будут одинаковы. Следовательно, приведенная длина физического маятника ─ это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

Дата добавления: 2014-01-20