
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 20. Основные теоремы о пределах. Понятие о неопределенностях и способах их раскрытия
Упражнения.
1. Доказать, что 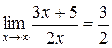 .
.
2. Найти пределы:
1)  ; 2)
; 2)  ; 3)
; 3) 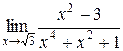 ; 4)
; 4) 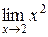 ;
;
5) 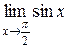 ; 6)
; 6) 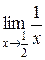 ; 7)
; 7)  ; 8)
; 8) 
Ответы: 1) 8; 2) 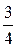 ; 3) 0; 4) 4; 5) 1; 6) 6; 7) 3; 8) 3.
; 3) 0; 4) 4; 5) 1; 6) 6; 7) 3; 8) 3.
На прошлой лекции мы дали определение бесконечно малой функции. Функция f(x) называется бесконечно малой при  или
или  , если
, если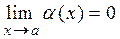 или
или  . Запишем это определение в другом виде: если
. Запишем это определение в другом виде: если 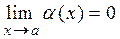 , то это значит, что для любого наперед заданного произвольно малого положительного числа
, то это значит, что для любого наперед заданного произвольно малого положительного числа 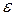 найдется
найдется 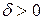 такое, что для всех х, удовлетворяющих условию
такое, что для всех х, удовлетворяющих условию 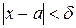 , будет удовлетворяться условие
, будет удовлетворяться условие 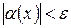 . Теперь обсудим некоторые свойства бесконечно малых функций, позволяющие доказать основные теоремы о пределах.
. Теперь обсудим некоторые свойства бесконечно малых функций, позволяющие доказать основные теоремы о пределах.
Свойство 1: Если функция y = f(x) представляется в виде суммы постоянного числа b и бесконечно малой : y = b+
: y = b+  (1), то limy=b (при
(1), то limy=b (при или
или  ). Обратно, если limy=b, то можно написать y = b+
). Обратно, если limy=b, то можно написать y = b+  , где
, где  - бесконечно малая.
- бесконечно малая.
Доказательство: из равенства (1) следует 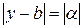 . Но при произвольном
. Но при произвольном 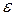 все значения
все значения  , начиная с некоторого, удовлетворяют соотношению
, начиная с некоторого, удовлетворяют соотношению  , следовательно, для всех значений y, начиная с некоторого, будет выполняться неравенство
, следовательно, для всех значений y, начиная с некоторого, будет выполняться неравенство 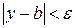 . Что и означает, что limy=b.
. Что и означает, что limy=b.
Обратно: если limy=b, топри произвольном 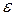 для всех значений y, начиная с некоторого, будет
для всех значений y, начиная с некоторого, будет 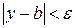 . Но если обозначим y - b=
. Но если обозначим y - b=  , то следовательно, для всех значений
, то следовательно, для всех значений  , начиная с некоторого будет выполняться
, начиная с некоторого будет выполняться  , а это значит, что
, а это значит, что  - бесконечно малая.
- бесконечно малая.
Свойство 2: Если 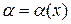 стремится к нулю при
стремится к нулю при  (или при
(или при  ) и не обращается в нуль, то
) и не обращается в нуль, то  стремится в бесконечность.
стремится в бесконечность.
Доказательство: при любом как угодно большом М>0 будет выполняться неравенство  , если только будет выполняться неравенство
, если только будет выполняться неравенство  . Последнее неравенство будет выполняться для всех значений
. Последнее неравенство будет выполняться для всех значений  , начиная с некоторого, так как
, начиная с некоторого, так как  .
.
Свойство 3: Алгебраическаясумма двух, трех и вообще определенного числа бесконечно малых есть функция бесконечно малая.
Доказательство: пусть 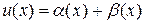 , где
, где 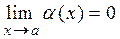 ,
,  . Докажем, что при произвольном, как угодно малом
. Докажем, что при произвольном, как угодно малом  найдется
найдется 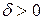 , такое, что при удовлетворении неравенства
, такое, что при удовлетворении неравенства 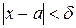 будет выполняться неравенство
будет выполняться неравенство  . Так как
. Так как 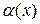 есть бесконечно малая, то найдется такое
есть бесконечно малая, то найдется такое  , что в окрестности с центром в точке а и радиусом
, что в окрестности с центром в точке а и радиусом  будет
будет  . Так как
. Так как 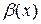 есть бесконечно малая, то найдется такое
есть бесконечно малая, то найдется такое 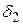 , что в окрестности с центром в точке а и радиусом
, что в окрестности с центром в точке а и радиусом 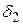 будет
будет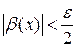 . Возьмем
. Возьмем 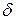 равным меньшему из величин
равным меньшему из величин  и
и 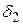 , тогда в окрестности точки а с радиусом
, тогда в окрестности точки а с радиусом 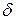 будут выполняться неравенства
будут выполняться неравенства  ;
; 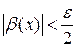 . Следовательно в этой окрестности мы имеем
. Следовательно в этой окрестности мы имеем 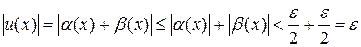 , т.е.
, т.е.  , что и требовалось доказать. Аналогично проводится доказательство и для случая, когда
, что и требовалось доказать. Аналогично проводится доказательство и для случая, когда  ,
,  .
.
Введем понятие ограниченной функции и приведем без доказательства еще два свойства. Функция y=f(x) называется ограниченной в данной области изменения аргумента х, если существует положительное число М такое, что для всех значений х, принадлежащих к рассматриваемой области, будет выполняться неравенство  . Если же такого числа не существует, то функция y=f(x) называется неограниченной в данной области. Функция y=f(x) называется ограниченной при
. Если же такого числа не существует, то функция y=f(x) называется неограниченной в данной области. Функция y=f(x) называется ограниченной при  , если существует окрестность с центром в точке а, в которой данная функция ограничена.
, если существует окрестность с центром в точке а, в которой данная функция ограничена.
Свойство 4: Произведение бесконечно малой функции 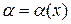 на функцию ограниченную z=z(x) при
на функцию ограниченную z=z(x) при  (или при
(или при  ) есть бесконечно малая функция.
) есть бесконечно малая функция.
Свойство 5: Частное 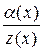 от деления бесконечно малой функции
от деления бесконечно малой функции 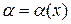 на функцию, предел которой отличен от нуля, есть бесконечно малая функция.
на функцию, предел которой отличен от нуля, есть бесконечно малая функция.
Вычислить предел функции, изучая поведение последовательности значений аргумента и функции, довольно легко для основных функций, таких, как  sinx, cosx, tgx, ctgx, arcsinx, arccosx, arctgx, arcctgx в их области определения, поскольку они непрерывны в своей области определения. Таким образом, в области определения предельное значение этих функций равно ее значению при предельном значении аргумента:
sinx, cosx, tgx, ctgx, arcsinx, arccosx, arctgx, arcctgx в их области определения, поскольку они непрерывны в своей области определения. Таким образом, в области определения предельное значение этих функций равно ее значению при предельном значении аргумента:
 .
.
В тех случаях, когда функция имеет сложный вид, т.е. составлена из нескольких других основных функций при помощи конечного числа алгебраических операций, вычисление значений функции может быть весьма утомительным и установление ее предела непосредственно затруднительным. При нахождении предела таких функций пользуются свойствами пределов функций. Сформулируем их.
1) Предел постоянной равен самой постоянной.
2) Постоянный множитель можно выносить за знак предела.
3) Пусть функции  имеют в точке
имеют в точке  конечные пределы, соответственно равные
конечные пределы, соответственно равные 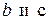 . Тогда функции
. Тогда функции

| 
| 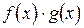
| 
| 
|
имеют в точке  пределы, соответственно равные
пределы, соответственно равные
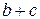
| 
| 
| 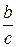
| 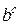
|
Докажем некоторые из этих свойств из пункта 3.
Теорема 1. Предел алгебраической суммы двух функций равен алгебраической сумме пределов этих функций.
Доказательство: пусть lim f(x)=b и limg(x)=c, тогда на основании первого свойства бесконечно малых функций можем написать: f(x)=b+ , g(x)=c+
, g(x)=c+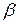 , где
, где  и
и 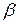 - бесконечно малые функции. Значит f(x)+g(x)= (b+c) +(
- бесконечно малые функции. Значит f(x)+g(x)= (b+c) +( ), т.к. (b+c) – есть постоянная величина, а (
), т.к. (b+c) – есть постоянная величина, а ( ) – величина бесконечно малая, тогда на основании того первого свойства бесконечно малых функций заключаем, что lim(f(x)+g(x))=b+c= lim f(x)+lim g(x), что и требовалось доказать.
) – величина бесконечно малая, тогда на основании того первого свойства бесконечно малых функций заключаем, что lim(f(x)+g(x))=b+c= lim f(x)+lim g(x), что и требовалось доказать.
Теорема 2. Предел произведения двух функций равен произведению пределов этих функций.
Доказательство: пусть lim f(x)=b и limg(x)=c, тогда на основании первого свойства бесконечно малых функций можем написать: f(x)= b+ , g(x)= c+
, g(x)= c+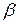 , где
, где  и
и 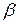 - бесконечно малые функции. Значит f(x)*g(x)=
- бесконечно малые функции. Значит f(x)*g(x)=  . Произведение bc – есть величина постоянная, а
. Произведение bc – есть величина постоянная, а 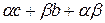 - бесконечно малая, на основании свойств бесконечно малых функций. Таким образом, по свойству 1 бесконечно малых функций получаем что lim(f(x)*g(x))=b*c= lim f(x)*lim g(x), что и требовалось доказать.
- бесконечно малая, на основании свойств бесконечно малых функций. Таким образом, по свойству 1 бесконечно малых функций получаем что lim(f(x)*g(x))=b*c= lim f(x)*lim g(x), что и требовалось доказать.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля.
Доказательство: пусть lim f(x)=b и limg(x)=c, тогда на основании первого свойства бесконечно малых функций можем написать: f(x)= b+ , g(x)= c+
, g(x)= c+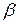 , где
, где  и
и 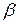 - бесконечно малые функции. Произведем следующие преобразования:
- бесконечно малые функции. Произведем следующие преобразования:  . Дробь
. Дробь  есть постоянное число, а дробь
есть постоянное число, а дробь  - бесконечно малая, на основании свойств бесконечно малых функций. Таким образом, по свойству 1 бесконечно малых функций получаем что lim(f(x)/g(x))=b/c= lim f(x)/lim g(x), что и требовалось доказать.
- бесконечно малая, на основании свойств бесконечно малых функций. Таким образом, по свойству 1 бесконечно малых функций получаем что lim(f(x)/g(x))=b/c= lim f(x)/lim g(x), что и требовалось доказать.
В тех случаях, когда либо 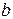 , либо
, либо 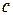 , либо оба вместе равны
, либо оба вместе равны 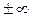 , или в частном
, или в частном  , применение указанных правил не дает возможности найти предел составной функции. Рассмотрим пример. Пусть
, применение указанных правил не дает возможности найти предел составной функции. Рассмотрим пример. Пусть
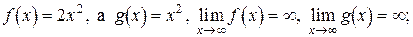
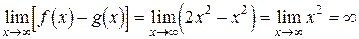 .
.
Возьмем теперь
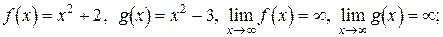
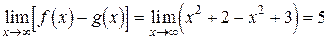 .
.
Рассмотрим и такой вид функций:
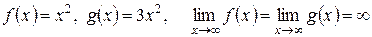 ,
,
 .
.
Такие ситуации, где значение предела зависит от конкретного вида функций участвующих в выражении, называются непределенностями.
Предел разности двух стремящихся к  функций, значение которого зависит от конкретного вида функций, называется неопределенностью вида
функций, значение которого зависит от конкретного вида функций, называется неопределенностью вида 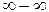 .
.
Предел частного двух функций, стремящихся к нулю, значение которого зависит от конкретного вида функций, называется неопределенностью вида 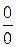 .
.
Аналогично определяются и другие неопределенности: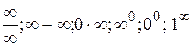 .
.
Пример 2. Найти  .
.
Решение. Воспользоваться равенством 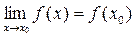 здесь нельзя, так как при
здесь нельзя, так как при  функция
функция 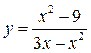 не определена (при
не определена (при  выражение
выражение 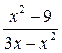 дает неопределенное выражение
дает неопределенное выражение  ). Значит, нужно анализировать поведение функции при
). Значит, нужно анализировать поведение функции при 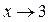 .
.
Функция 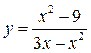 представляет собой дробь, у которой при
представляет собой дробь, у которой при 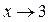 и числитель, и знаменатель одновременно стремятся к нулю. Но стремление числителя дроби к нулю ведет к уменьшению этой дроби, а стремление знаменателя к нулю – наоборот, к ее увеличению. Какой фактор перевесит – пока неясно, в разных случаях бывает по-разному. То есть в данном пределе имеется неясность (неопределенность) типа
и числитель, и знаменатель одновременно стремятся к нулю. Но стремление числителя дроби к нулю ведет к уменьшению этой дроби, а стремление знаменателя к нулю – наоборот, к ее увеличению. Какой фактор перевесит – пока неясно, в разных случаях бывает по-разному. То есть в данном пределе имеется неясность (неопределенность) типа  . Кстати, это не единственный возможный тип неопределенности, но о прочих типах – позже.
. Кстати, это не единственный возможный тип неопределенности, но о прочих типах – позже.
Неопределенность, встретившуюся при вычислении предела, нужно раскрывать. То есть как-то так преобразовать выражение под знаком предела, чтобы неопределенность исчезла и предел стал очевиден. В частности, раскроем нашу неопределенность:
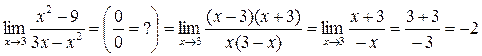
Пример 3. Найти 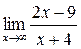 .
.
Решение. Здесь при 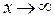 и числитель, и знаменатель дроби стремятся к бесконечности. Но стремление числителя дроби к бесконечности ведет к неограниченному росту дроби, а стремление знаменателя дроби к бесконечности, наоборот, ведет к неограниченному уменьшению дроби (к стремлению ее к нулю). Эти два фактора, как и в предыдущем примере, работают друг против друга, приводя к неопределенности типа
и числитель, и знаменатель дроби стремятся к бесконечности. Но стремление числителя дроби к бесконечности ведет к неограниченному росту дроби, а стремление знаменателя дроби к бесконечности, наоборот, ведет к неограниченному уменьшению дроби (к стремлению ее к нулю). Эти два фактора, как и в предыдущем примере, работают друг против друга, приводя к неопределенности типа  . Раскроем её:
. Раскроем её:
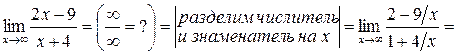
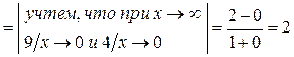 .
.
Неопределенности типа  и
и 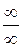 принадлежат к числу наиболее часто встречающихся при вычислении пределов неопределенностей. Но есть как уже говорилось есть и другие типы неопределенностей. Всего этих типов семь:
принадлежат к числу наиболее часто встречающихся при вычислении пределов неопределенностей. Но есть как уже говорилось есть и другие типы неопределенностей. Всего этих типов семь:
1) 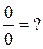 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; (1)
; (1)
5)  ; 6)
; 6)  ; 7)
; 7) .
.
Эти записи нужно понимать не буквально, не как арифметические операции с символами 0 и ¥, а как предельные ситуации при вычислении пределов. Для сравнения приведем другие предельные ситуации, неопределенностями не являющиеся:
1)  ; 2)
; 2) 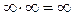 ; 3)
; 3)  ; 4)
; 4) 
( ;
;  ;
;  ;
; 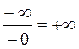 )
)
5)  ; 6)
; 6)  .
.
Если при вычислении предела функции возникает какая-либо из неопределенностей (1), ее нужно как-то раскрывать. Если неопределенности нет, значит, ситуация ясная, и результат следует записать сразу.
Пример 4. Найти  .
.
Решение.

Пример 5. Найти  .
.
Решение.
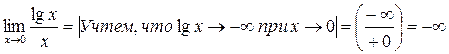
Помимо теорем о пределах функций, непосредственно позволяющих вычислять пределы, интерес представляют еще ряд теорем о пределах. Они используются далее при выводе замечательных пределов и при исследовании функций. Приведем их без доказательства.
Теорема 4. Если между соответствующими значениями функций u=u(x), z=z(x), v=v(x) выполняются неравенства 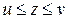 , при этом u(x) и v(x) при
, при этом u(x) и v(x) при  (или при
(или при  ) стремятся к одному и тому же пределу b, то z=z(x) при
) стремятся к одному и тому же пределу b, то z=z(x) при  (или при
(или при  ) стремится к тому же пределу.
) стремится к тому же пределу.
Теорема 5. Если при  (или при
(или при  ) функция y принимает неотрицательные значения
) функция y принимает неотрицательные значения 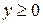 и при этом стремится к пределу b, то b есть неотрицательное число:
и при этом стремится к пределу b, то b есть неотрицательное число:  .
.
Теорема 6. Если между соответствующими значениями двух функций u=u(x), v=v(x), стремящихся к пределам при  (или при
(или при  ), выполняется неравенство
), выполняется неравенство  , то имеет место
, то имеет место  .
.
Теорема 7. Если функция возрастает v=v(x), т.е. всякое её последующее значение больше предыдущего, и если она ограничена, т.е.  , то эта функция имеет предел lim v=a, где
, то эта функция имеет предел lim v=a, где 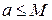 .
.
|
Дата добавления: 2014-01-20; Просмотров: 361; Нарушение авторских прав?; Мы поможем в написании вашей работы!