
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод переменных состояния
|
|
|
|
Это единственный из методов формирования ММС, который позволяет получить математическую модель в нормальной форме Коши. Рассмотрим получение ММС на примере механической системы (рис.1)

|
Рис. 1.
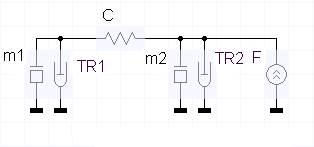
1. Составляем эквивалентную схему (рис.2).
|
Рис. 2.
2. Строим граф эквивалентной схемы (рис.3) Граф практически повторяет эквивалентную схему, но без условных изображений ветвей.

|
Рис. 3.
3. Выбираем нормальное дерево графа. Нормальное дерево — это фундаментальное дерево (не образующее контуров), в которое ветви включены согласно приоритету E,C,R,L,I (в соответствии с аналогиям физических однородных подсистем). В данном случае в качестве ветвей дерева нужно использовать ветви m1 и m2. (рис.4)

|
Рис. 4.
4. Строим матрицу контуров и сечений, где столбцы соответствуют ветвям дерева, а строки — хордам.
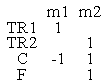
5. Для получения топологических уравнений сканируем М-матрицу по строкам и столбцам. При сканировании по строкам получаем уравнения непрерывности (неразрывности), при сканировании по столбцам - уравнения равновесия. При получении уравнений непрерывности знаки элементов матрицы меняются на противоположный.
VTR1=-Vm1
VTR2=-Vm2
Vc=Vm1-Vm2
VF=-Vm2
Fm1=FTR1-Fc
Fm2=FTR2+Fc+F
6. Добавляем компонентные уравнения всех ветвей.
FTR1= КTR1VTR1
FTR2= КTR2VTR2
 =
= Fm1
Fm1
 =
=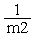 Fm2
Fm2
 =CVc
=CVc
7. Получаем нормальную форму Коши, раскрывая правые части последних трех уравнений
 =
= (FTR1-Fc)=
(FTR1-Fc)= (КTR1VTR1-Fc)=
(КTR1VTR1-Fc)= (КTR1(-Vm1)-Fc)
(КTR1(-Vm1)-Fc)
 =
=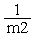 (FTR2+Fc+F)=
(FTR2+Fc+F)=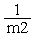 (КTR2VTR2+Fc+F)=
(КTR2VTR2+Fc+F)=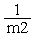 (КTR2(-Vm2)+Fc+F)
(КTR2(-Vm2)+Fc+F)
 =C(Vm1-Vm2)
=C(Vm1-Vm2)
Далее, используя численный метод интегрирования, получаем переходные процессы.
Примечание 1. Нормальная форма Коши не может быть получена если в ветви дерева попадет ветвь типа L или в хорды - ветвь типа C.
Узловой метод получения ММС (var1)
|
|
|
Метод развивался в домашинное время в электротехнике как метод узловых потенциалов и в строительной механике как метод перемещений.
1. Исходная информация вводится в виде эквивалентной схемы.
2. Составляется матрица инцидентности А=(aij), которая содержит информацию о структуре схемы (что с чем соединено). Если i – номер узла, j – номер ветви,
aij =(+/-)1, если узел i и ветвь j инцидентны. Иначе 0.
(+) если в ветви направление тока к узлу
(-) если направление тока от узла.
Пример: принц схема??
Эквивалентная схема
Узлы C1 C2 R1 R2 R3 L1 J
1 0 0 -1 0 0 0 1
2 -1 0 +1 -1 0 0 0
3 0 0 0 +1 -1 +1 0
4 0 -1 0 0 +1 0 0
Матрица инцидентности
3. Составляется матрица проводимости ветвей y = dI/dU
- Резистивная ветвь yi =1/Ri
- Источник тока yi = 0
- Емкостная ветвь Iс = С dU/dt. Производится замена конечными разностями In = C (Un –Un-1)/h, h – шаг интегрирования. In = y Un + q, где y = c/h,
q = - c/h Un-1 .
- Индуктивная ветвь Un = L (In – In-1)/ h. In = y Un + q, где y = h/L и
q = In-1
В общем виде I = Y U + Q -набор компонентных уравнений.
В развернутом виде:
Uc1 Uc2 UR1 UR2 UR3 UL1 UJ1
IC1 C1/h -C1/h U1n-1
IC2 C2/h -C2/h U2n-1
IR1 1/R1 1/R1 U1
IR2 1/R2 1/R2 U2
матрица узловых проводимостей вектор невязок
A – матрица узловых проводомостей В – вектор невязок
4. Записываем топологические уравнения в матричной форме: сумма токов - узла равна 0
A I = 0
Подставляем вместо тока его значение из матричной формы компонентных уравнений
A Y U + A Q = 0
Переходим от напряжений к потенциалам
U = Aт Фи(фи1, фи2, …)
A Y Aт Фи = A Q
или Я Фи = A Q, где Я – матрица Якоби
Эта система и решается на каждом шаге интегрирования.
Ограничения классического узлового метода:
- в схемах не должно источников напряжения
- в аргументах зависимых ветвей могут быть только потенциалы
В программах анализа, использующих модифицированный узловой метод, эти ограничения сняты за счет усложнения СЛАУ
Модифицированный узловой метод лежит в основе блоков анализа эквивалентных схем программ PA-9, OrCad, МicroCap, Adams.
|
|
|
Узловой метод (var2)
Базис узлового метода составляют переменные типа потенциала, в дальнейшем узловые потенциалы. В основе узлового метода лежит уравнение равновесия
 (
( )=
)=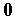 - сумма переменных типа потока в узлах эквивалентной схемы равна нулю.
- сумма переменных типа потока в узлах эквивалентной схемы равна нулю.
Данное выражение представляет собой систему нелинейных алгебраических уравнений, для решения которой воспользуемся методом Ньютона. Для нахождения неизвестного вектора  поступим следующим образом. Будем считать, что известно некоторое приближеное решение
поступим следующим образом. Будем считать, что известно некоторое приближеное решение  и необходимо найти поправку к нему
и необходимо найти поправку к нему  , то есть
, то есть
 =
=  +
+ 
Разложим функцию в ряд Тейлора и оставим в разложении только два члена
 (
( ) =
) =  (
( +
+  )=
)= (
( )+
)+ =
= 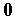
Для нахождения поправки необходимо решить систему линейных алгебраических уравнений
 (
( )
) =-
=- (
( ) (1)
) (1)
где  (
( )=
)= - матрица узловых проводимостей,
- матрица узловых проводимостей,  (
( ) - вектор невязок
) - вектор невязок  вектор поправок.
вектор поправок.
после этого считаем  =
= +
+ и снова формируем и решаем систему (1).Цикл заканчивается при выполнении условия
и снова формируем и решаем систему (1).Цикл заканчивается при выполнении условия

 ε1 или
ε1 или  (
( )
)
 ε2 или по комбинации этих условий или неудачно по превышению числа итераций.
ε2 или по комбинации этих условий или неудачно по превышению числа итераций.
Выражение (1) и есть математическая модель объекта в узловом базисе. То есть, для его получения необходимо сформировать матрицу узловых проводимостей и вектор невязок.
Рассмотрим формирование ММС для схемы представленной на рис.1
|
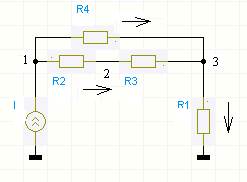
Рис. 1.
Будем считать ток положительным, если он вытекает из узла, в противном случае - отрицательным. Направления токов в пассивных элементах могут быть заданы произвольно, если они не совпадут с действительным направлением, то получим значение тока со знаком минус. Размерность математической модели определяется числов узлов схемы минус 1, то есть в нашем случае равна трем.

 = -
= -
G=1/R с соответствующим индексом.
Отдельный элемент тоже можно рассматривать как схему, например резистор (рис.2)

|
Рис. 2.
Математическая модель этого объекта будет выглядеть следующим образом:

 = -
= - 
Как можно видеть для ММС схемы рис.1 каждый элемент типа R дает аддитивный вклад в общую математическую модель, в соответствии с узлами подключения.
Такой же аддитивный вклад можно определить для произвольного многополюсного элемента.
Как следует из (1) допустимый вид компонентного уравнения - I=I(φ). То есть напрямую узловой метод может быть применен к анализу статических состояний. Но одна из основных задач анализа объекта на макроуровне - это получение временных диаграмм работы устройств, то есть анализ динамики. Динамические процессы в объекте определяются реактивными элементами типа С и L. Если привести компонентные уравнения элементов С и L к виду I=I(φ),то можно говорить и об анализе динамики. Компонентное уравнение элемента типа С I= C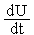 дискретизируем с помощью какого-либо метода численного интегрирования, например, с помощью с помощью неявного метода Эйлера
дискретизируем с помощью какого-либо метода численного интегрирования, например, с помощью с помощью неявного метода Эйлера 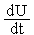 =
=
|
|
|
I=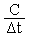 (U-Un-1)=
(U-Un-1)=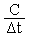 (φi-φj)-
(φi-φj)-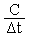 Un-1
Un-1
Таким образом, на одном шаге численного интегрирования получили компонентное уравнение в допустимом виде, и модель элемента типа С может быть представлена следующим образом:

 = -
= - 
Аналогично для элемента типа L.
U=L =
= (I-In-1) или I=In-1+
(I-In-1) или I=In-1+ (φi-φj)
(φi-φj)

 = -
= - 
Достоинства узлового метода:
1. Малая размерность математической модели
2. Простой алгоритм формирования ММС
3. Простые алгоритмы работы с многополюснымии элементами, что позволяет разрабатывать библиотеки ММЭ с вложенными элементами
Недостатки узлового метода:
1. Ограничение на вид компонентного уравнения.
2. Методы численного интегрирования ОДУ растворены в компонентных уравнениях реактивных ветвей.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 851; Нарушение авторских прав?; Мы поможем в написании вашей работы!