Холл эффектісі

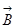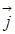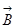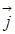Сыртқы магнит өрісінің индукция сызықтарына перпендикуляр орналастырлыған өткізгіш пластинаның (1.2-сурет) бойымен тығыздығы ток жүргенде, пластинаның астыңғы және үстіңгі жақтары арасында потенциалдар айырымы, яғни мен бағыттарына перпендикуляр бағытта электр өрісі пайда болады. Бұл құбылыс Холл эффектісі деп аталады. Бұл эффектіні магнит өрісінде қозғалатын электр зарядтарына әсер етуші Лоренц күші арқылы түсіндіруге болады.

1.2-сурет. Холл эффектісінің сұлбасы.

Ток тығыздығының 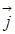бағыты суреттегідей белгілі болса,оңнан солға қарай қозғалыс жасайтын электронға әсер ететін Лоренц күші жоғары қарай бағытталған. Пластинаның жоғарғы жағында – электрондардың молдығы, ал пластинаның төменгі жағында – электрондардың жетіспеушілігі болады. Сонымен, пластиналардың арасында төменнен жоғары қарай бағытталған көлденең электр өрісі пайда болады.Бұл өрістің кернеулігі Лоренц күшін теңгере алатын шамаға жеткенде, көлденең бағытта зарядтардың стационар таралып жайғасуы орнайды. Бұл жағдайда:

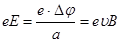немесе 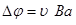, (1.14)

мұндағы 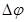– Холл эффектісі нәтижесінде пайда болатын көлденең потенциалдар айырмасы; а – пластинаның қалыңдығы; u – электрондардың реттелген қозғалысының орташа жылдамдығы. Ток күшін І, өткізгіштің бірлік көлеміндегі зарядтар санын n және олардың қозғалыс жылдамдығы арасындағы қатынасты пайдаланып, өткізгіштегі электрондардың реттелген қозғалысының орташа жылдамдығын табамыз:

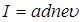, бұдан ,

мұндағы d – пластина ені, n – электрондардың концентрациясы. Жылдамдықтың u бұл мәнін (1.14) теңдеуіне қоятын болсақ:

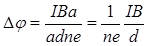. (1.15)

Бұл (1.15) формулада – затқа тәуелді Холл тұрақтысы.

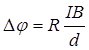. (1.16)

Көлденең потенциалдар айырымы ток күшіне (І), магнит өрісі индукциясына (B) тура пропорционал да, пластина қалыңдығына (d) кері пропорционал. Холл тұрақтысы белгілі болса, ол арқылы өткізгіштік сипаты мен тасымалдаушылардың заряды белгілі жағдайда, өткізгіштегі ток тасымалдаушылардың концентрациясын анықтауға болады. Холл тұрақтысының таңбасы ток тасымалдаушылардың зарядының е таңбасымен бірдей болғандықтан, Холл тұрақтысы бойынша шала өткізгіштердің өткізгіштік табиғаты туралы тұжырым айтуға болады.

1.5 Вакуумдағы магнит өрісі үшін 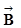векторының циркуляциясы.

Толық ток заңы

Берілген тұйық контур бойымен 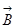векторының циркуляциясы деп мына интегралды айтады:

(1.17)

мұндағы 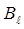=Вcosa - контурға жанама бағытындағы 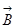векторының құраушысы, - контурдың элементар ұзындық векторы (контурды айналып өту бағытындағы), a - 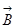және векторлары арасындағы бұрыш. Бұл интеграл тогы бар түзу өткізгіштің магнит өрісі үшін оңай есептелінеді. Бұл контурдың әрбір нүктесінде 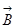векторы модуль бойынша бірдей, шеңберге жанама бойымен бағытталған. 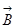векторының циркуляциясы мынаған тең:

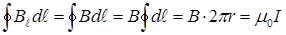. (1.18)

Егер контур токты қамтымаса, 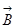векторының циркуляциясы нөлге тең болады. Кез келген пішінді өткізгіш арқылы жүретін ток үшін де бұл теңдеуді пайдалануға болатынын дәлелдеуге болады. Вакуумдағы магнит өрісі үшін толық ток заңын тұжырымдайық: кез- келген тұйық контур бойынша 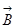векторының циркуляциясы магнит тұрақтысын m₀ осы контурды қамтитын токтардың алгебралық қосындысына көбейткенге тең болады:

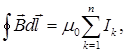(1.19)

мұндағы n – пішіні еркін алынған контурмен қамтитын тогы бар өткізгіштердің жалпы саны.

1.6 Магнит индукциясы векторының ағыны.

Магнит өрісі үшін Гаусс теоремасы

dS ауданы арқылы өтетін магнит индукциясының ағыны (не магнит ағыны) деп 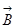магнит индукциясын ds ауданы мен ауданға түсірілген нормаль және магнит индукциясы векторының арасындағы a бұрышының косинусына көбейткенге тең скаляр физикалық шаманы айтады:

=BScosα, (1.20)

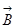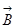мұндағы B_n = Bcosa – векторының dS ауданына түсірілген нормаль бағытына түсірілген проекциясы, a – мен векторларының арасындағы бұрыш, – бағыты ауданға түсірілген нормальдің бағытымен бағыттас бірлік аудан векторы, вектордың модулі dS-ке тең.

Магнит ағыны – алгебралық шама, ол оң (dФ>0) және теріс (dФ<0) болуы мүмкін. Ағынның таңбасы cosa-нің таңбасына тәуелді және нормальдің оң бағытын таңдап алынумен анықталады. Егер ағын ток жүретін контурмен байланысты болса, контурға түсірілген нормальдің оң бағыты ток бағытымен оң бұрғы ережесі бойынша байланысқан. Бұл кезде cosa>0 және магнит ағыны dФ>0.

Еркін алынған бет S арқылы өтетін магнит индукциясы векторының ағыны:

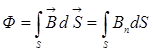. (1.21)

Өріс біртекті болса (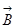=const), ал бет жазық болып және 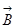векторына перпендикуляр орналасса, онда B_n=B=const және

. (1.22)

Магнит ағынының өлшем бірлігі – «Вебер»

(Вб): 1Вб – индукциясы 1 Тл біртекті магнит өрісіне перпендикуляр орналасқан ауданы 1м² жазық бетті қиып өтетін магнит ағыны .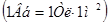

Магнит индукциясы векторының ағыны контур ауданын қиып өтетін магнит өрісі күш сызықтарының санына тең.

Магнит өрісі 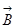үшін Гаусс теоремасы: кез келген тұйық бет арқылы өтетін магнит индукция векторының ағыны нөлге тең:

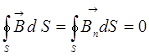. (1.23)

Бұл тұжырым табиғатта магнит зарядтарының жоқ екендігін және магнит индукция сызықтарының тұйықталғандығын көрсетеді.

1.7 Магнит өрісінде тогы бар өткізгішті

орын ауыстырғанда атқарылатын жұмыс

Қозғалмайтын сымдар мен олардың үстімен жылжитын сым бөлігінен тұратын тогы бар контурды қарастырайық. Егер мұндай контур оның жазықтығына перпендикуляр болатын біртекті магнит өрісінде орналасатын болса, онда сым бөлігі Ампер күші әсерінен орын ауыстыра бастайды. Демек, магнит өрісі - тогы бар өткізгіш орын ауыстырғанда жұмыс атқарады.

Өткізгіш бөлігіне әсер ететін күш 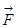оңға қарай бағыттылған, ол F = ІВ l, мұндағы l – өткізгіш бөлігінің ұзындығы.

Өткізгіш бөлігі dx -қа орын ауыстырғанда, Ампер күші оң жұмыс атқарады:

dA = Fdx =І Bldx = ІBdS = ІdФ,

мұндағы dS=ldx – магнит ағыны қиып өтетін аудан, 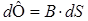– ауданын қиып өтетін магнит индукциясы векторының ағыны.

Сонымен, магнит өрісінде тогы бар өткізгішті орын ауыстырғанда істелетін жұмыс - ток күшін қозғалатын өткізгішті қиып өтетін магнит ағынына көбейткенге тең:

dA = ІdФ. (1.26)

Бұл формуланы бағыты еркін алынған 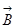векторы үшін де қолдануға болады.

Нег. 2[ 114-148], 7[226-245 ], 8 [ 204-22].

Қос. 22 [ 133-153], 48 [ 183-194].

Бақылау сұрақтары:

1. Тұрақты ток өрісінің магниттік индукциясы қалай есептеледі?

2. Толық ток заңына сүйеніп, қандай жағдайларда магнит индукциясын табу ыңғайлы болып табылады?

3. Орам саны бар дөңгелек токтың центріндегі магнит өрісінің индукциясы неге тең?

2-дәріс

ЗАТТАРДАҒЫ МАГНИТ ӨРІСІ

Магнетиктер деп магниттік қасиеттері қарастырылатын кез-келген денелерді айтады. Магнетиктер магнит өрісін қоздыруға не өзгертуге қабілетті.Магнетиктерді сыртқы магнит өрісіне енгізгенде магнетиктердің магниттелуі өз кезегінде осы өрісті өзгертеді. Әртүрлі магнетиктердің қасиеттерін, олардың магнит өрісінің индукциясының шамасына әсерін түсіндіру үшін, магнит өрісінің заттардың атомдары мен молекулаларына әсерін зерттеу қажет.

2.1 Электрондар мен атомдардың магнит моменттері

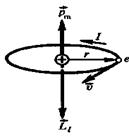Магнит өрісіне енгізілген кез келген зат ерекше күйге келеді – ол магниттелінеді. Бұл құбылысты Ампер гипотезасы негізінде түсіндіруге болады: кез келген денедегі атомдар мен молекулалардағы электрондардың қозғалысы нәтижесінде микроскопиялық токтар пайда болады. Классикалық физиканың қағидаларына байланысты атомдағы электрондар оң зарядтты ядро маңында тұйық орбиталармен қозғалады (2-1.Сурет). Әр электронның мұндай қозғалысы тұйық контурда ағатын токқа эквивалентті. Сондықтан, кез келген атомды не молекуланы олардың магниттік қасиеттері жөнінен магнит өрісі кеңістігіндегі электрондық микротоктардың қайсыбір жиынтығы ретінде қарауға

болады.

2.1-сурет. Электронның тұйық орбита бойымен қозғалысы.

Жаңа физикалық шамалар ұғымын енгізейік. Электронның орбиталық магнит моменті деп тұйық орбитада электрондардың қозғалысынан пайда болатын электр тогының магнит моменті 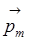айтылады. Электронның орбиталық магнит моменті мынаған тең:

p_m=ІS=eνs, (2.1)

мұндағы S – электрон орбитасымен шектелген аудан; І – ток күші; n – электронның орбитадағы айналу жиілігі; е – электрон зарядының абсолют мәні. Ток күші (І) бірлік уақытта тасымалданатын зарядқа тең болғандықтан, орбита бойымен айналатын электрон мынадай ток күшін тасымалдайды:

І=en. (2.2)

Жиілік 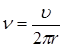, мұндағы 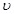– электрон жылдамдығы; r – орбита радиусы. Онда ток күші:

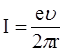. (2.3)

Электронның магнит моменті:

. (2.4)

Бұл формула атомдағы кез келген электрон үшін дұрыс. Магнит моменті 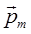– векторлық шама, оның бағыты тогы бар орамның магнит өрісінің индукциясы бағытымен бірдей болады. Магнит моментінің бағыты оң бұранда ережесімен анықталады. 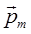векторының ұшынан орамдағы ток сағат тілі қозғалысына қарсы бағытпен айналатын болып көрінеді. Молекуланың не атомның орбиталық магнит моментінің векторы 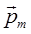деп осы молекулалардағы не атомдардағы барлық электрондардың орбиталық магнит моменттерінің векторлық қосындысын айтамыз:

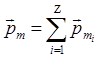, (2.5)

мұндағы z – Д.И. Менделеевтің периодтық жүйесіндегі элементтердің реттік нөмірі, ол әр элементтердегі жалпы электрон санын береді. Орбитамен қозғалатын электрон механикалық импульс моменттеріне де ие, оның модулі:

, (2.6)

мұндағы 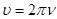r, 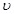– жылдамдық, S = pr² – ауданы десек, онда

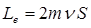. (2.7)

Электронның орбиталық механикалық моменті 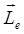векторының бағыты оң бұранда ережесімен анықталады:

, (2.8)

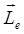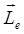(2.8) қатынас гиромагниттік қатынас деп аталады. Мұндағы минус таңбасы және векторларының қарама-қарсы бағытталғанын көрсетеді. Атомдағы әртүрлі орбиталар үшін электронның жылдамдығы мен орбита радиустары r бірдей емес, олай болса мен векторлары да әртүрлі болады, бірақ гиромагниттік қатынас тұрақты шамалармен анықталатындықтан кез-келген орбиталар үшін бір мәнді болады.

2.2 Магниттелу. Заттағы магнит өрісі

Магнетиктердің магниттелу дәрежесі магниттеліну деп аталатын векторлық шамамен сипатталады. Магнетиктің бірлік көлеміндегі магнит моментін- магниттеліну деп атаймыз

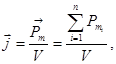(2.9)

мұндағы – магнетиктің магнит моменті, ол сан жағынан жеке молекулалардың магнит моменттерінің қосындысына тең. Магнетиктер токтардың магнит өрісінде магниттеледі де өзінің меншікті магнит өрісі пайда болады. Нәтижесінде өрістің магнит индукциясының векторы

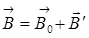, (2.10)

мұндағы 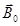– сыртқы өрістің вакуумдегі магнит индукциясы; 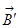– молекулалық токтардың беретін магнит индукциясы. Вакуумдегі токтың туғызған магнит өрісінің индукция векторы макротоктардың магнит өрісін сипаттайтын кернеулікпен былай байланысады:

,

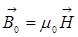мұндағы m₀ – магнит тұрақтысы. Тәжірибеден кеңістікті толығымен толтырып тұрған біртекті нөлден өзгеше өрістегі магнетикте 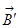- индукция (парамагнетиктер) векторымен бағыттас немесе қарама-қарсы (диамагнетиктер) болуы мүмкін. 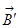векторын 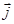магниттелумен байланыстырайық. Бұл байланысты қарапайым дербес жағдай үшін орындайық. Көлденең қимасы S, ұзындығы l,цилиндр тәрізді біртекті магнетикті қарастырайық, ол индукциясы В₀ біртекті магнит өрісінде орналассын. Магнетик реттелген молекулалық токтардың болуынан магниттеледі.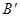пен 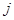арасындағы байланыс:

,

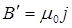немесе векторлық түрде

. (2.11)

Қорытқы өрістің магнит индукциясын табамыз:

(2.12)

немесе

.

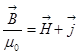Әлсіз өрістерде магниттелу берілген сыртқы токтардың өрістерінің (магниттейтін өрістің) кернеулігіне тура пропорционал екені тәжірибеден белгілі:

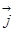= χ , (2.13)

мұндағы χ – заттың магнит сезімталдығы деп аталатын, қарастырылатын магнетикті сипаттайтын өлшемсіз шама. Сонымен,

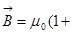χ), (2.14)

бұдан

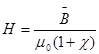. (2.15)

(1 + χ) өлшемсіз шаманы m әрпімен белгілеу қабылданған,

1 + χ = m, (2.16)

оны ортаның магнит өтімділігі деп атайды.Осы айтылғандарды ескерсек:

. (2.17)

Алынған өрнектер тек біртекті магнетиктер үшін ғана орынды. Магнит сезімталдылығы χ – заттардың сыртқы магнит өрісінің әсерінен магнит моментін өзгерте алу қабілеттілігін сипаттайтын физикалық шама. Егер магнит өрісінде зат болмаса, онда 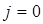, яғни вакуум үшін χ =0. Вакуум үшін m=1 болғандықтан, магнит тұрақтысы m₀ вакуумның магнит өтімділігі деп аталады. Магнит сезімталдылығы χ <0 және абсолют шамасы жағынан аз магнетиктер диамагнетиктер деп аталады. Диамагнетиктер үшін m<1. Магнит сезімталдылығы χ>0 (m>1) және шама жағынан аз болатын магнетиктер парамагнетиктер деп аталады. Магнетиктердің тағы бір түрі бар – олар ферромагнетиктер, олар үшін χ >0 және өте үлкен мәнге ие бола алады. Егер диа- және парамагнетиктерде χ=const болса, ферромагнетиктерде магниттік сезімталдылығы магнит өріс кернеулігінің функциясы болып табылады:

χ =¦(H). Магниттелу векторы парамагнетиктерде бағыты жағынан сыртқы магнит өрісінің бағытымен бағыттас болса, ал диамагнетиктерде қарсы бағытталған болып келеді.

Дата добавления: 2014-01-20