Главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси

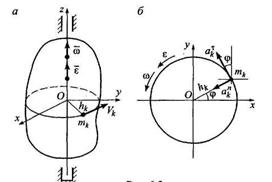Вычислим координаты главного момента сил инерции твердого тела, вращающегося вокруг неподвижной оси. Ось Oz совместим с осью вращения, а оси Ох и Оу скрепим с вращающимся телом, тогда 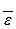(0,0, ε) и (0,0, ω), r_k(x_k;y_k;z_k) - радиус-вектор рассматриваемой точки т_к. При вращении тела вокруг неподвижной оси Oz ускорение любой точки т_к состоит из нормального ускорения и касательного ускорения , где h_k - расстояние точки k от оси вращения Oz:

;

;

.

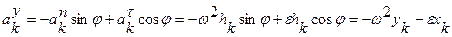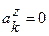Здесь учтено, что h_kcosφ = x_k, h_ksinφ = у_к, х_к и у_к - координаты точки т_к.

Тогда, согласно (6.12), получим,

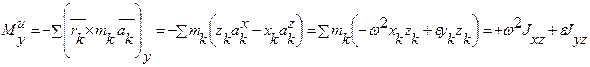
Здесь J_xz, J_yz - центробежные моменты инерции, J_z - осевой момент инерции.

Таким образом, главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси, сводится к паре сил, момент которой равен

где

, ,

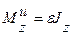
Если ось вращения проходит через центр тяжести тела и оси Oxyz являются главными осями, то

, ,

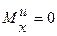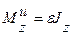
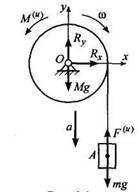Пример 3. Через блок весом Mg и радиу­сом R перекинута нерастяжимая нить, на конце которой подвешен груз А весом mg. Определить ускорение а груза А, натяжение нити Т и давление на подшипник оси блока.

Решение. Пусть груз А опускается вниз, тогда сила инерции груза вверх: F^и = ma.

Поскольку ось вращения диска является осью симметрии, то J_xz=J_yz = 0. Следовательно, момент от сил инерции, равен 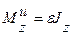и направлен в сторону противоположную вращению диска.

Отбросим опору О, заменим ее действие реакциями подшипника R_x и R_y. Составим уравнения кинетостатики:

, ;

, ;

, .

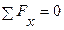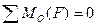Подставим в последнее уравнение значения силы инерции F^(u)=ma и момента от сил инерции 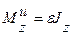= (J/R)a, где t = a/R, и решим его относительно ускорения а.

Получим

, .

Тогда из первых двух уравнений (а) определим

,

Для определения натяжения нити разорвем гибкую связь и заменим ее действие натяжением Т. Добавляя внешнюю силу mg и силу инерции F^(и), имеем

-mg+F^(u)+T = 0,

откуда T = mg- F^(и) = m(g - а) = .

Если считать диск сплошным телом, то J_z - —mR², тогда

, , , .

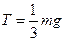Лекция 16 (Аналитическая механика)

«Связи и их классификация. Обобщенные координаты,

Работа силы на возможном перемещении»

В основу классической механики положены понятия пространства, времени, силы и массы. Она оперирует векторными величинами, векторными уравнениями и их проекциями на координатные оси. Аналитическая механика построена на основных принципах, основанных на сравнении движений. Этот принцип изучает мгновенное состояние движения и возможные отклонения от этого состояния, допускаемые связям в данный момент времени. В аналитической механике широко применяются скалярные меры движении материальных объектов и меры их действия (кинетическая энергия, работа сил и т.д.).

Основы изложения аналитической механики составляют некоторые общие принципы, из которых аналитическим путем получаются дифференциальные законы движения на основе которых изучается движение твердых тел и системы материальных точек.

СВЯЗИ И ИХ КЛАССИФИКАЦИЯ

Система материальных точек называется свободной, если положение отдельных её точек и их скорости могут принимать произвольное значение. Несвободной - если на положение и скорости точек системы наложены ограничения геометрического или кинематического характера, называемыми связями.

Связями называют любого вида ограничения, налагаемые на положения (координаты) и скорости точек механической системы.

Конструктивно связи осуществляются в виде нитей, стержней, шарниров, опор, поверхностей и т.д. Аналитически связи выражаются уравнениями или неравенствами, т.е. соотношениями между радиус - векторами точек системы, их скорости и времени. Связи можно разделить на два типа: удерживающие (двухсторонние) и неудерживающие (односторонние). Удерживающими связями называются связи, которые сохраняют свое действие во все время движения точек системы. Аналитически эти связи выражаются уравнениями, связывающие координаты точек, их скорости и время

,

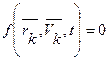здесь - радиус вектор, определяющий положение k -той точки системы, - ее скорость, t - время.

Примером удерживающей связи может служить система из двух материальных точек т₁ и т₂, которые соединены стержнем постоянной длины L. В этом случае уравнение связи имеет вид

.

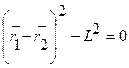Неудерживающими связями называются связи, которые могут в некоторые промежутки времени меняться. Аналитически они выражаются неравенством, связывающим координаты точек системы, их скорости и время

.

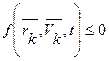Примером неудерживающей связи может служить система из двух материальных точек, которые соединены гибкой нитью длинной L. В этом случае уравнение связи имеет вид

/

В дальнейшем будем рассматривать только удерживающие связи.

Связь называется стационарной, если она не меняется с течением времени. В уравнение стационарной связи не входит время t в явном виде.

Примером механизма, имеющего стационарные связи, может служить кривошипно-шатунный механизм. Механизм состоит из кривошипа ОА длинной r, шатуна АВ длинной L и ползуна В.

Уравнения связи данного механизма запишутся:

,

.

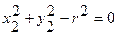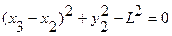Первое уравнение определяет постоянную длину кривошипа, второе - постоянную длину шатуна.

Связь называется нестационарной, если она меняется с течением времени. Уравнение такой связи содержит время t явно.

Например, материальная точка может двигаться только по поверхности. Пусть уравнение поверхности задано в виде функции f(х,у,z) = 0. Это стационарная связь. Если поверхность подвижная или деформирующаяся, то в уравнение поверхности время г войдет явно: f(х,у,z,t) = 0. В этом случае связь нестационарная. Примером нестационарной связи является, также деформируемое твердое тело.

Связь называется конечной или геометрической, если она накладывает ограничения только на координаты точек системы. Уравнение конечной (геометрической) связи имеет вид

.

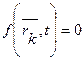Эта связь не налагает ограничение на скорости точек системы.

В общем случае удерживающая связь называется кинематической или дифференциальной. Эта связь налагает ограничения на положение координат точек системы и на скорости этих точек.

Если кинематическая (дифференциальная) связь интегрируется, то после интегрирования связь перестает быть таковой и становиться конечной (геометрической) связью. Следовательно, связь будет кинематической (дифференциальной) только в том случае, если она неинтегрируемая.

Система называется склерономной, если на нее наложены только стационарные связи. В противном случае система называется реономной.

Голономной называется всякая свободная система материальных точек, а также несвободная система с конечными или дифференциальными, но интегрируемыми связями. При наличии дифференциальных неинтегрируемых связей, система называется неголономной.

Рассмотрим пример голономной связи. Колесо радиуса R катиться без скольжения по прямолинейному рельсу.

Положение колеса в плоскости движения хОу определяется координатами центра колеса (полюса) х_с, у_с и углом поворота φ. Если

ось Ох направить вдоль рельса, то у_с = R, следовательно, наложено ограничение на координату у, связь - конечная (геометрическая).

Кроме того, должна быть равна нулю скорость точки Р, точки касания колеса с рельсом. Это условие запишется в виде уравнения .. Последнее уравнение накладывает ограничения на скорости, поэтому связь будет дифференциальной (кинематической). Но это уравнение сразу интегрируется и приводит к соотношению между координатами х_с и φ, имеющему вид х_с=Rφ. Таким образом, рассмотренная система является голономной.

В качестве примера неголономной связи рассмотрим движение конька по поверхности льда. При отсутствии скольжения вектор скорости центра тяжести конька С должен быть направлен по касательной к траектории движения - по оси т

Имеем: 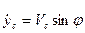, где φ - угол, образованный осью х и касательной к траектории движения в точке С - осью 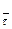. Разделив второе соотношение на первое, получим 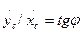, откуда 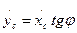. Таким образом получено уравнение, накладывающее ограничения на скорость. Это уравнение не может быть проинтегрировано, поскольку угол φ - переменный (угол φ=φ(t) определяет направление оси 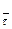, поэтому это уравнение является уравнением неголономной связи.

Дата добавления: 2014-01-20