Пример 3. Для системы образующих примера 2 формулы обратных преобразований имеют вид:

Для системы образующих примера 2 формулы обратных преобразований имеют вид:

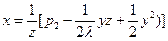
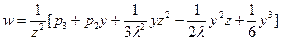
В качестве примера этих преобразований рассмотрим задачу выражения собственного полинома 2-ой степени 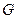от переменных 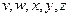через систему образующих . Пусть

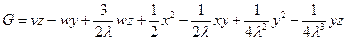
Вычислим преобразования каждого из мономов 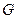. Получим:

.

.

.

.

.

.

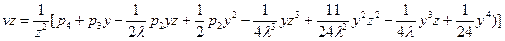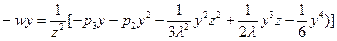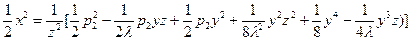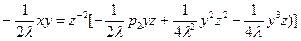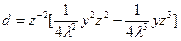Просуммируем полученные равенства и выделим полином, не зависящий от :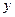

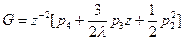
Это и есть представление 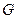в системе собственных образующих 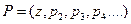. Осталось проверить, что все коэффициенты при мономах, зависящих от 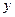, равны .

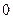4. Собственные полиномы и 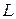-инварианты линейных операторов

Пусть - произвольный невырожденный линейный оператор, действующий на векторном пространстве однородных многочленов как линейное преобразование переменных , 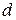- натуральное число и . Множество собственных полиномов степени 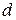от переменных из 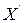образует конечномерное векторное подпространство, которое мы обозначим через 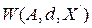. Базис этого подпространства состоит из конечного числа полиномов .

Отметим, что для операторов – жордановых клеток теорема 4 дает описание этого базиса через полиномы набора 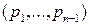. Именно,

,

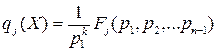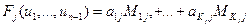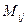, , - мономы от переменных .

Пусть 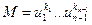- такой моном. Тогда 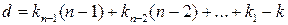. В принципе, базис подпространства 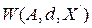можно вычислить методом неопределенных коэффициентов, однако вычислительная сложность этого алгоритма – полином от 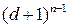. Поэтому задачу эффективного конструктивного описания базиса 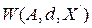следует считать открытой.

В частности, один из вопросов может быть сформулирован таким образом: пусть множество базисных мономов задано формулой

.

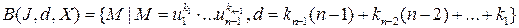Очевидно, 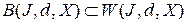. Является ли это множество базисом 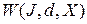? Например, является ли множество

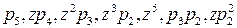
(примеры 2, 3) базисом подпространства ?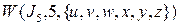

Для каждой жордановой клетки 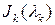жордановой формы оператора определена своя последовательность подпространств собственных полиномов. Пусть 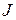- одна такая клетка. Тогда, в обозначениях, используемых выше при рассмотрении операторов – жордановых клеток, эта последовательность имеет вид

.

Собственным числом подпространства 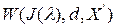назовем число 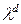. Последовательность собственных чисел рассматриваемых подпространств имеет вид . Если жорданова форма оператора состоит из нескольких клеток, в определении подпространств собственных полиномов , очевидно, имеет смысл рассматривать только подмножества переменных вида , где - подмножества переменных, соответствующих данной жордановой клетке оператора , а объединение берется по всем жордановым клеткам оператора .

Рассмотрим линейный оператор, образованный двумя жордановыми клетками 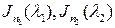. Любое подпространство собственных полиномов оператора в этом случае является прямым произведением подпространств жордановых клеток:

.

Через 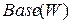обозначим базис подпространства 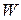. Тогда

.

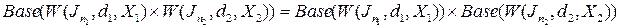Если

,

,

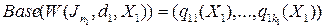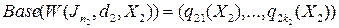то

,

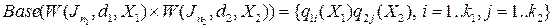а собственное число этого подпространства равно 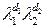. Эта конструкция непосредственно распространяется на операторы, содержащие произвольное количество жордановых клеток произвольных размеров.

Если жорданова форма линейного оператора состоит из жордановых клеток 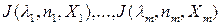, т.е.

,

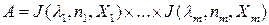для оператора можно выделить систему подпространств собственных полиномов, каждое из которых характеризуется собственным числом , .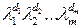

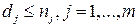Теорема 5. Если собственные числа двух подпространств собственных полиномов линейного оператора равны, их сумма также образует подпространство собственных полиномов:

.

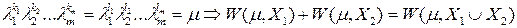Доказательство очевидно.

Ниже мы покажем, что определение подпространств собственных полиномов – одна из наиболее важных задач теории программных инвариантов линейных операторов.

Рассмотрим теперь задачу построения 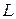- инвариантов линейных операторов (см. определение 1). Пусть оператор состоит из одной жордановой клетки и 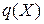- собственный полином с собственным числом 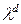. Тогда, очевидно, рациональное выражение

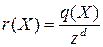
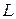- - инвариант . Таким образом, для жордановой клетки размера 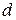существует по крайней мере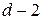 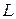- инварианта

. (18).

Эти инварианты мы будем называть внутриклеточными.

Замечание 3. Система L-инвариантов (18), определяемая через собственные многочлены, задает т.н. орбиту линейного оператора 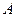в пространстве 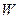. В самом деле, если вектор 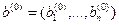выбран как начальный, последовательность векторов, заданная рекуррентным соотношением 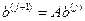, лежит в двумерном алгебраическом многообразии, заданном системой уравнений

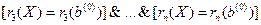(19)

Можно ожидать, что орбита 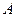, как бесконечная последовательность, лежит в одномерном многообразии, причем недостающим членом системы (19) должно быть уравнение, задаваемое L-инвариантом, зависящим от 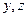. Следствие к лемме 1 показывает, что таких инвариантов не существует. Однако, легко проверить, что неалгебраическая функция

удовлетворяет соотношению (6): 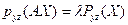. Поэтому к алгебраической системе (19) можно добавить неалгебраическое уравнение, получив описание одномерного многообразия, содержащего орбиту :

.

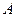Теорема 5 определяет так называемые межклеточные инварианты. Именно, пусть пространство собственных полиномов произвольного линейного оператора содержит два различных подпространства 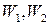с равными собственными значениями (т.е. удовлетворяют теореме 5), . Тогда

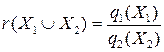
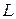- - инвариант оператора .

Теорема 6. Пусть 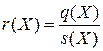- L-инвариант линейного оператора . Тогда - собственные полиномы с равными собственными числами.

Доказательство. Мы можем считать, что дробь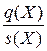несократима.

.

Поскольку несократимые дроби в поле рациональных выражений 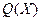представляются в виде отношения целых выражений единственным образом с точностью до числового множителя,

.

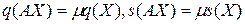Теорема доказана.

В заключение сформулируемосновную теорему об 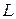- инвариантах линейных операторов:

Теорема 7. Пусть 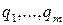- множество всех базисных полиномов всех жордановых клеток линейного оператора и 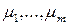- совокупность их собственных чисел. Предположим, что существуют такие целые числа 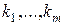, что

. (20)

Тогда

- L-инвариант линейного оператора .

Доказательство очевидно.

Таким образом, проблема описания L-инвариантов линейного оператора сводится к проблеме описания всех соотношений (20). В [10, 11] доказано, что это множество имеет конечный базис.

Если все собственные числа линейного оператора - рациональные числа, проблема построения этого базиса алгоритмически разрешима с помощью теоретико-числового алгоритма.

В случае, когда 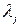- алгебраические числа, проблема построения базиса множества соотношений (2) остается открытой.

Литература

1. Годлевский А.Б., Капитонова Ю.В., Кривой С.Л., Летичевский А.А. Итеративные методы анализа программ // Кибернетика. – 1984. – №2, С.23-28.

2. A.Letichevsky, M.Lvov. Discovery of invariant Equalities in Programs over Data fields. Applicable Algebra in En­­­gi­neering, Communi­ca­tion and Computing. – 1993. – №4. – pp. 21-29

3. Львов М.С. Инвариантные равенства малых степеней в программах, опеределенных над полем. // Кибернетика. – 1988. - №1. – С. 108 – 110.

4. Львов С.М. О реализации вычислений в задачах анализа программ, определенных над векторными пространствами // Проблемы программирования – 2004.-№№2-3. Специальный выпуск. С. 95-101.

5. Львов М.С. Инвариантные неравенства в програм­мах, интерпретированных над упоря­до­ченными полями. // Кибернетика. – 1986. – №5. – С.22-27

6. Müller-Olm M., Seidl H. Computing polynomial program invariants. // Inf. Process. Lett. September 2004.- Vol 91, Issue 5. Elsevier North-Holland, Inc. Amsterdam. - pp. 233-244.

7. Sankaranarayanan S., Sipma H., Manna Z. Non-linear loop invariant generation using Gröbner bases.// Proc. of Symposium on Principles of Programming Languages. - Venice, Italy, January 14-16, 2004. ACM: New York, NY, USA, 2004.- pp. 318-329.

8. Rodríguez-Carbonell E., Kapur D. Automatic generation of polynomial loop invariants: algebraic foundations. // Proc. Of International Symposium on Symbolic and Algebraic Computation.- Santander, Spain, July 4-7, 2004.- ACM: New York, NY, USA 2004.- pp. 266-273.

9. Rodríguez-Carbonell E., Kapur D. Automatic generation of polynomial invariants of bounded degree using abstract interpretation. // Sci. Comput. Program. Volume 64, Issue 1 (January 2007).- Elsevier North-Holland, Inc. Amsterdam, The Netherlands.- 2007.-pp.54-75.

Дата добавления: 2014-01-20