Определение I

Истинность высказывания с квантором существования устанавливается при помощи конкретного примера. Чтобы убедиться в ложности такого высказывания, необходимо провести доказательство.

Истинность высказывания с квантором общности устанавливается путем доказательства. Показать ложность таких высказываний можно, приведя контрпример.

Доказательство истинности высказываний, содержащих квантор общности, можно выполнять различными методами (рассуждения, перебор всех возможных вариантов и др.). Привести пример.

Заметим, что убедиться в ложности высказывания – это значит опровергнуть его.

В начальной школе высказывания с кванторами общности изучаются в неявном виде. Например, изучая свойства арифметических действий, дети узнают, что:

Ø Делить на 0 нельзя

Ø При умножении на 1 получается то же самое число, что и умножали ("аÎN) а×1=а

Ø При вычитании разность всегда меньше уменьшаемого (а-b=c, где с< а)

Ø При сложении, если к какому-либо (т.е. любому) числу прибавить 1, то получится последующее число.

При изучении данных правил учитель делает акцент на то, что все эти свойства арифметических действий характерны для любых чисел натурального ряда, и приводит в пример свои примеры:

Ø 2×1=2, 3×1=3, 5×1=5, 28×1=28 и т.д.

Ø 15-7=8, где 8<15; 32-11=21, где 21<32 и т.д.

Ø 3+1=4, 4+1=5, 47+1=48, 632+1=633 и т.д.

При изучении свойств геометрических фигур, например в теме «Квадрат. Площадь квадрата» дети знакомятся с признаком квадрата:

Ø «у квадрата все стороны равны, у квадрата 4 угла», который также характерен для любого (каждого) квадрата;

Ø также учитель показывает детям, что формула нахождения площади применима для квадрата любого размера. В качестве доказательства учитель рисует на доске несколько квадратов разного размера, показывая в каждом квадрате его признак, а затем находит площади этих фигур, показывая тем самым, что формулу эту можно применять к абсолютно любому квадрату.

При изучении правил в математике, учитель на основе закона коммутативности сложения (в начальных классах этот закон рассматривается как правило) «от перемены мест слагаемых сумма не меняется», тоже использует высказывание с квантором общности, т.к. это правило подходит для любых чисел натурального ряда. Учащиеся могут самостоятельно доказать это правило своими примерами:

15+8=23 17+4=21 6+19=25

8+15=23 4+17=21 19+6=25 и др.

Важно, чтобы дети сами сказали, что это свойство выполняется при сложении любой (всякой, каждой) пары чисел.

Или, например, при изучении правила прибавления числа к сумме (для того, чтобы прибавить число к сумме, можно прибавить это число к первому слагаемому суммы, а затем к полученному результату прибавить 2 ^е слагаемое. Учитель также подчеркивает, что данное правило характерно для любых чисел из натурального ряда, и показывает это на примере: (17+21)+3=(17+3)+21=41 и т.д.

Задания на знание точного смысла слов: и, или, все, каждый, некоторые.

Для уточнения смысла указанных слов целесообразно использовать первые уроки.

С помощью контрольных вопросов (заданий) выясняется, правильно ли дети понимают смысл слов: и, или, все, каждый. В случае затруднений учащихся необходимо раскрыть смысл указанных слов. Ввести слова все, каждый при выполнении, например, следующих заданий:

1) Обведите на одной строчке 3 клетки. Раскрасьте их. Вопросы: сколько клеток обвели? Сколько клеток раскрасили? (3 клетки обвели и 3 раскрыли. Можно сказать также, что обвели 3 клетки и все раскрасили, а можно сказать и по-другому: обвели 3 клетки и каждую раскрасили).

Для проверки понимания смысла введенных слов можно предложить следующие задания:

2) У Маши было 4 яблока. Все яблоки она отдала сестре?

3) Нарисуйте 5 флажков. Каждый из них раскрасьте красным карандашом. Сколько флажков нарисовали? Сколько флажков раскрасили? Почему? (Нарисовали 5 флажков и каждый раскрасили. Значит, раскрасили 5 флажков).

Умение правильно использовать слова: и, или, все, каждый, некоторые формируется при выполнении заданий, аналогичных следующим:

4) а) Верно ли, что все треугольники – красные; все круги – синие; некоторые круги – синие; каждый треугольник – красный; все квадраты – белые?

б) Выбери из слов все, некоторые, каждый нужное и запиши его вместо точек, чтобы предложения были верными:

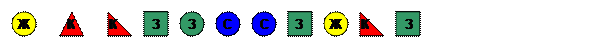
…… треугольники – красные, …… круги – синие, …… квадрат – зеленый.

5) Учитель дал детям задание. Один ученик выполнил задание так:

Другой ученик выполнил то же самое задание так:

Учитель проверил и сказал, что оба ученика выполнили задание правильно.

Подумайте, каким было задание. Выберите правильный ответ из предложенных:

а) нарисуйте 3 квадрата и 2 треугольника. Раскрасьте 3 квадрата и 2 треугольника;

б) нарисуйте 3 квадрата или 2 треугольника. Раскрасьте 3 квадрата и 2 треугольника;

в) нарисуйте 3 квадрата или 2 треугольника. Раскрасьте 3 квадрата или 2 треугольника

г) нарисуйте 3 квадрата и 2 треугольника. Раскрасьте 3 квадрата или 2 треугольника.

Для нахождения ответа учащиеся могут для каждого из предложенных ответов дать интерпретацию и путем сравнения с данными рисунками указать правильный ответ.

Вопрос 3. Понятие дедуктивного умозаключения. Простейшие схемы дедуктивных умозаключений. Примеры дедуктивных умозаключений из начального курса математики. Обучение доказательству младших школьников.

Дедукция (от лат. deductio – выведение) – вывод по правилам логики; цель умозаключений (рассуждений), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) Д. являются аксиомы, постулаты или просто гипотезы, имеющие характер общих утверждений (“общее”), а концом – следствия из посылок, теоремы (“частное”). Если посылки Д. истинны, то истинны и её следствия. Д. – основное средство доказательства.

Дата добавления: 2014-01-20