Поиск и составление плана решения задачи

Анализ задачи.

Основное назначение этапа – понять в целом ситуацию, описанную в задаче; назвать известные и искомые объекты, выделить все отношения (зависимости) между ними.

Известно несколько приёмов, которые можно использовать при анализе задачи.

а) Задать официальные вопросы и ответить на них:

О чем задача?

Что требуется найти в задаче?

Что обозначают те или иные слова в тексте задачи?

Что в задаче неизвестно?

Что является искомым?

б) Приём перефразировки текста задачи.

Он заключается в замене данного в задаче описания некоторой ситуации другим, сохраняющим все отношения, связи, качественные характеристики, но более явно их выражающим. Отбрасывается несущественная, излишняя информация, заменяются описания некоторых понятий соответствующими терминами; преобразовывается текст задачи в форму, удобную для поиска плана решения. Перефразированный текст часто бывает полезно записать в таблице.

Назначение этапа: установить связь между данными и исходными объектами, наметить последователь­ность действий. Одним из наиболее известных приемов поиска плана решения является разбор задачи по тексту или по ее вспомогательной модели:

От данных к вопросу.	От вопроса к данным.
Решающий выделяет в тексте задачи 2 данных и на основе связи между ними определяет, какое неизвестное м.б. найдено по этим данным и с помощью какого арифм. действия. Затем, считая это это неизв. данными вновь выделяет 2 взаимосвязанных данных, опред. неизвестные и т.д., пока не будет выяснено, какое действие приводит к получению искомого в задаче объекта.	Нужно обратить внимание на вопрос задачи и установить, что достаточно узнать для ответа на этот вопрос. Затем выяснить, есть ли для этого необходимые данные. Если нет, то установить, что нужно знать, чтобы найти недостающие данные и т.д.

Поиск плана решения задачи может производиться по вспомогательной модели, выполненной при анализе задачи.

3. Осуществление плана решения.

Назначение этапа: найти ответ на требование задачи, выполнив все действия в соответствии с планом.

Приемы:

- запись по действиям (с пояснением, без пояснения, с вопросами);

- запись в виде выражения.

4. Проверка решения задачи.

Назначение этапа: установить правильность или ошибочность выполнения решения.

Приемы:

- Установление соответствия между результатом и условиями задачи (результат вводится в текст задачи и на основе рассуждений устанавливается, не возникает ли противоречия).

- Решение задачи другим способом.

Понятие «задача» в начальном курсе математики.

При обучении младших школьников математике решению текстовых задач уделяется большое внимание, т.к.:

1. В сюжетах находят отражение практические ситуации, имеющие место в жизни ребёнка.

2. Решение этих задач позволяет ребёнку осознать практическую значимость тех математических понятий, которыми он овладевает в начальном курсе математики.

3. В процессе их решения у ребёнка можно формировать умения, необходимые для решения любой математической задачи.

Вот, например, простейшая схема – введение в анализ задачи (1 класс.).

2 3	условие
?	вопрос
2+3=5	решение
	ответ

Она создается на первых уроках при разборе задачи в картинках: В вазе лежало 2 яблока. Мама положила туда еще 3 яблока. Сколько яблок стало в вазе? Цель таблицы – оставить наглядный след при первом объяснении элементов задачи. Выводу схемы сопутствуют вопросы учителя – “Что в задаче известно? Что мы знаем?" Хором говорим – “Мы знаем, что в вазе было 2 яблока, и мы знаем, что мама положила туда еще 3 яблока”. При этом учитель заполняет рамку таблицы на доске и сообщает, что это условие задачи. Мы выделили условие задачи. Что спрашивается в задаче? Сколько яблок стало в вазе? (Схема на доске дополняется знаком вопроса). Это вопрос задачи. Мы выделили вопрос задачи. Сколько же яблок стало в вазе? – спрашивает учитель. Пять, - отвечают дети. Как узнали? Что сделали? К двум прибавили три. Запись на доске продолжается (2+3=5). Это решение. Вы сказали решение задачи. Сколько же стало яблок в вазе, скажите еще раз. (5). “5“ – это ответ. Мы сказали ответ задачи. Далее учитель подводит детей к обобщению только что проведенного анализа задачи: Какие же части, элементы задачи мы выделили? (условие, вопрос, решение, ответ). Схема дополняется этими словами. На следующем уроке схема перед глазами детей. Задание учителя: Назовите части задачи. Далее ребята учатся составлять задачу по картинке, выделять условие, вопрос, решение и ответ задачи.

В настоящее время существует множество методических рекомендаций, связанных с обучением младших школьников решению задач.

Вопрос о том, как научить детей устанавливать связи между данными и искомыми в текстовой задаче и в соответствии с этим выбрать, а затем выполнить арифметические действия, решается в методической науке по-разному. Все многообразие методических рекомендаций, связанных с обучением младших школьников решению задач рассматривается с точки зрения 2^х принципиально отличающихся друг от друга подходов.

Один подход нацелен на формирование у учащихся умения решать задачи определенных типов (видов). Дети сначала учатся решать простые задачи, а затем составные, включающие в себя различные сочетания простых задач. При этом подходе многие учащиеся решают задачи лишь по образцу. А, встретившись с задачей незнакомого типа, заявляют: “А мы такие задачи не решали”. В этом огромный недостаток первого подхода.

Дети сначала учатся решать простые задачи, а затем составные, включающие в себя различные сочетания простых задач. М.А. Бантова и Г.В. Бельтюкова выделяют 3 группы простых задач:

1. Задачи, при решении которых дети усваивают конкретный смысл каждого из арифметических действий.

2. Задачи, при решении которых учащиеся усваивают связь между компонентами и результатами арифметических действий.

3. Простые задачи, при решении которых раскрывается понятия разности и кратного отношения.

Разнообразить урок позволяют следующие виды задач (по Царевой)

1) Задачи, не требующие полного решения.

2) Установление соответствия между задачей и графической моделью.

3) Выбор среди данных задач нужной (3 задачи – 1 рисунок)

4) Выбор подходящей схемы (1 задача – 3 схемы)

5) Нахождение ошибок в схеме.

6) Классификация простых задач по действиям, которыми они могут быть решены.

7) Выбор задач, ответ на вопрос которых может быть найден в заданной последовательности действий.

8) Обнаружение ошибок в решении.

9) В качестве творческого задания можно предлагать детям придумать задачу по графической схеме.

Цель другого подхода – научить детей выполнять семантический и математический анализ текстовых задач, выявить взаимосвязи между условием и вопросом, данными и искомыми и представлять эти связи в виде схематических и символических моделей. При этом подходе процесс решения задач (простых и со-ставных) рассматривается как переход от словесной модели к модели математической или схематической. В основе осуществления этого подхода лежит математический анализ текста. Учащиеся должны быть подготовлены к этой деятельности, поэтому знакомству младших школьников с текстовой задачей должна предшествовать специальная работа по формированию математических понятий и отношений. Также необходимо сформировать у младших школьников (до знакомства с задачей) те логические приемы мышления (анализ и синтез, сравнение, обобщение), которые обеспечивали бы их мыслительную деятельность в процессе решения задач. При этом подходе значительно сложнее подготовительная работа, но решение задач более осмысленно.

Вопрос 5. Определение отношений "больше на…" и "меньше на…" на множестве натуральных чисел, их теоретико-множественный смысл и способы моделирования. Методика формирования понятий "больше на…" и "меньше на…" в начальном курсе математики. Обучение младших школьников решению текстовых задач с данными отношениями.

В основе определения отношений «больше на» и «меньше на» лежит. понятие равночисленности множеств Например, чтобы утверждать, что 6 больше 4 на 2, сравнивают два множества, устанавливая взаимно-однозначное соответствие между множеством Х, в котором 4 элемента, и подмножеством У₁ другого множества У, в котором 6 элементов, и делают вывод: треугольников столько же, сколько кружков, и еще 2. Другими словами, треугольников на 2 больше, чем кружков.

Для установления отношений «больше», «меньше», «равно» между числами младшие школьники могут использовать предметные, графические и символические модели. Установление взаимно-однозначного соответствия между элементами двух множеств выступает в качестве математической основы действий на предметном уровне.

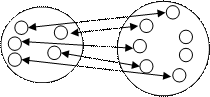С понятиями «больше на» и «меньше на» учащиеся знакомятся на первых уроках в первом классе в процессе установления взаимно-однозначного соответствия между предметными множествами. Для установления взаимно-однозначного соответствия между предметными множествами используют:

1. Наложение элементов одного множества на элементы другого:

Каких фигур больше?

Каких фигур меньше?

На сколько больше?

На сколько меньше?

2. Расположение элементов одного множества под элементами другого:

Каких фигур больше?

Каких фигур меньше?

На сколько больше?

На сколько меньше?

3. Образование пар, т. е. соединение элемента одного множества с одним элементом другого:

Каких фигур больше?

Каких фигур больше?

На сколько больше?

На сколько меньше?

Понятия «больше на», «меньше на» используются для случаев присчитывания и отсчитывания по единице при знакомстве с новым числом. В результате выполнения различных упражнений на каждом отрезке натурального ряда чисел, связанных с получением следующего числа (5+1=6; 6-1=5), дети убеждаются в том, что числа упорядочены по величине: после числа 1 называют при счете число 2, которое больше него на 1; перед числом 2 называют число 1, которое меньше него на 1 и т.п.

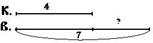
При обучении младших школьников решению текстовых задач с данными отношениями используют графическое моделирование и установление взаимно-однозначных соответствий. Например, задача: «Коля сделал 4 флажка, а Витя – 7 флажков. На сколько флажков Витя сделал больше».

1. Рисунок: 2.Условный рисунок:

3. Чертеж: 4.Схематичный чертеж:

Отношение «больше на» означает, что во множестве флажков, сделанных Витей, столько же элементов, сколько их во множестве флажков, сделанных Колей и еще 4.

Учителю необходимо подвести детей к выводу: чтобы узнать, на сколько одно число больше или меньше другого, можно из большего вычесть меньшее.

Дата добавления: 2014-01-20