Погрешности полунатурного моделирования

При полунатурном моделировании система управления замыкается через преобразующее устройство,как показано на рис.2.3, где обозначено: Wo(p) – передаточная функция разомкнутой системы управления (вместе с объектом управления), Wp(p) – передаточная функция преобразующего устройства [Л5.1].?

Пусть

Wo(p) = B(p)/A(p), Wp(p) = (1+G(p))/(1+Q(p))

B(p) =, A(p) =, an= 1 (2.3.1)

G(p) =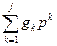, Q(p) =,

При идеальном преобразующем устройстве, когда Wp(p) = 1, передаточная функция замкнутой системы имеет вид:

WI(p) = B(p)/[A(p) + B(p)],

а характеристическое уравнение

RI(p) = A(p) +B(p) =0. (2.3.2)

Корни характеристического уравнения (23) будем считать известными и обозначим

pI1, pI2, …pIn (2.3.3)

Характеристическое уравнение передаточной функции преобразующего устройства, и его корни, в соответствии с (22), запишем:

Rp(p) = 1 + Q(p) = 0,

pp1, pp2…ppr (2.3.4)

Коэффициенты полинома Q(p) будем считать малыми, так, что модули корней (25) много больше модулей корней (24).В пределе, при Q(p) => 0,

limQ=>0[pIj] =

Передаточная функция замкнутой системы (см.рис. 2.3.) с учетом преобразующего устройства и ее характеристическое уравнение имеют вид:

W(p) = B(p)(1 + Q(p))/[A(p)(1+Q(p))+B(p)(1+G(p))]

R(p) = [A(p)(1+Q(p))+B(p)(1+G(p))] = 0 (2.3.5)

Характеристическое уравнение (5) имеет n + r корней:

p1, p2…pn,pn+1…pn+r

Представляется очевидным, что при Q(p)0 и G(p)0 первые n корней уравнения (5) стремятся к корням уравнения (2), а последние r корней стремятся в бесконечность по отрицательной полуоси, как и корни уравнения (4).

Это позволяет предположить, что характеристический полином R(p) (5) при малых Q(p) и G(p) незначительно отличается от произведения:

R1(p) = RI(p)Rp(p) (2.3.6)

Введем мало измененные полиномы R, входящие в (6):

RI (p) = RI(p) + d RI(p), Rp (p) = Rp(p) + d Rp(p), (2.3.7)

R1 (p) = RI (p) Rp (p), dRI(p) = dA(p) + dB(p), dRp(p) = dQ(p)

Здесь

dA(p) =, dB(p) =,

dQ(p) =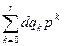. (2.3.8)

Величины dak…dqkявляются малыми приращениями соответствующих коэффициентов.

Приравняем теперь характеристический полином (5) измененному полиному (6):

R(p) = RI (p), (2.3.9)

Подставив сюда выражения (7) для приращений полиномов, сокращая одинаковые слагаемые и пренебрегая произведениями малых приращений, получим:

dA +dB + QdB + AdQ +BdQ = - B(Q – G) (2.3.10)

Левая и правая части этого уравнения являются полиномами по p с наибольшей степенью pn+r. Для выполнения равенства (10) при любых p нужно приравнять коэффициенты при одинаковых степенях p в левой и правой частях уравнения, что даст n+r соотношений между приращениями dak, dbk, dqk. Количество этих приращений, в соответствии с выражениями (8), равно n+r+m+1. Следовательно, для выполнения равенства (10) можно задать произвольно m+1 приращение, что позволяет принять

dB = 0. Тогда соотношение (10) приобретет следующий вид:

(1 + Q)dA + (A + B)dQ = - B(Q – G) (2.3.11)

Система алгебраических уравнений, эквивалентная полиномиальному уравнению (11), - линейная и, в общем случае, неоднородная. Однако, при выполнении условий

Q(p) = G(p), (2.3.12)

она станет однородной, т.е. будет иметь тривиальное нулевое решение dA(p) = 0, dQ(p) = 0. Этот результат становится очевидным, если вспомнить, что при выполнении условий (12) передаточная функция преобразующего устройства

Wp(p) = 1, что видно из (1).

Другой способ решения уравнения (11) исходит из того, что для обеспечения равенства двух полиномов степени (n+r) достаточно обеспечить их равенство в (n+r) точках по аргументу p. Для p, равных корням (3) уравнения(2), соотношение (11) приобретает вид:

dA(pIj)(1 + Q(pIj)) = -B(pIj)(Q(pIj) – G(pIj)); j = 1…n (2.3.13)

С учетом обозначений (7), систему уравнений (13) можно записать:

da0+ da1pIj+…dan-1pIjn-1= (2.3.14)

= -{ B(pIj)(Q(pIj) – G(pIj))}/ (1 + Q(pIj)); j = 1…n

Решение системы уравнений (14) дает приращения коэффициентов полинома A(p) и, в силу соотношения dB = 0, приращения коэффициентов полинома RI(p) = 0 (2).

Зная приращения коэффициентов полинома (2), можно вычислить приращения его корней по соотношениям (2.2.8).

Сравнивая (2.2.8) с (14) можно видеть, что в них входят одинаковые комбинации приращений коэффициентов, поэтому не нужно решать (14) относительно dak, а можно сразу вычислять приращения основных корней системы по формуле

dpIj= {B(pIj)(Q(pIj) – G(pIj))}/ (1 + Q(pIj))(pIj- pI1)*

*(pIj- pI2)… (pIj- pIn), j = 1…n (2.3.15)

Подставив в (11) корни (4), получим:

dQ(ppj)[A(ppj) + B(ppj)] = -B(ppj)(Q(ppj) – G(ppj));

j = 1…r (2.3.16)

Проведя аналогичные предыдущим рассуждения и выкладки, получим приращения остальных корней:

dppj= B(ppj)(Q(ppj) – G(ppj))/ [A(ppj) + B(ppj)]*

*(ppj– pp1) … (pIj- pIn); j = 1…r (2.3.17)

Итак, включение в моделирующий комплекс динамического преобразующего устройства приводит к тому, что характеристическое уравнение модели имеет две группы корней: основные - мало измененные корни уравнений идеальной системы, и дополнительные - мало измененные корни характеристического уравнения преобразующего устройства.

Задавая допустимое смещение основных корней, а также допустимое сближение основной и дополнительной групп, можно предъявить требования к быстродействию преобразующего устройства.

Раздел 3 Упражнения

Колебательное звено без затухания описывается дифференциальным уравнением:

(3.1)

При идеальном выполнении математических операций такое звено совершает незатухающие гармонические колебания с частотой w. Использование вычислительной техники для моделирования такого звена может привести к затухающим или раскачивающимся колебаниям с измененной частотой. Изменение частоты и декремент затухания (раскачки) при моделировании могут являться мерой погрешности выполнения математических операций.

Определить теоретически погрешность по частоте и декремент затухания (раскачки) в зависимости от шага интегрирования для первых четырех порядков метода рядов Тейлора.

Решить уравнение (3.1) методами Рунге – Кутта первых четырех порядков. Определить фактическую частоту и декремент затухания (раскачки), сравнить с результатами п.1).

Произвести предварительную коррекцию уравнения (3.1), определить теоретические значения частоты и затухания (раскачки).

Решить скорректированное уравнение (3.1) методами Рунге – Кутта первых четырех порядков, сравнить с результатами п.3).

Вычислить смещение корней уравнения (3.1) при аналоговом моделировании с передаточной функцией интегратора (2.2.15). Найти границу по моделируемой частоте w, отделяющую затухание от раскачки.

Промоделировать уравнение (3.1) на аналоговой модели, сравить с результатами п.5).

Включить в схему моделирования уравнения (3.1) преобразующее устройство с передаточной функцией

W(p) = 1/(1+Tp)

Вычислить изменение частоты и декремент раскачки. Предъявить требования к допустимому значению T в зависимости от w.

Литература

Л5.1. Боевкин В.И. Оценка точности математического моделирования динамических систем. – М.: Изд. МГТУ, 1990. – 54 с.

Л5.2. Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.

Л5.3. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. - М.: Мир, 1980. – 279 с.

Л5.4. Беки Дж., Карплюс У. Теория и применение гибридных вычислительных систем. – М.: Мир, 1970. – 483 с.

Л5.5 Боевкин В.И., Багдамян О. Н. Оценка точности решения задачи Коши по смещению корней характеристического уравнения. – Труды №474. – М.: МВТУ, 1987. – 82 с.

Л5.6 Стренг Г. Линейная алгебра и ее применения. – М.: Мир, 1980. - 454 с.

Л5.7. Анисимов В.В., Голубкин В. Н. Аналоговые вычислительные машины. – М.: Высш. школа, 1971. – 447 с.

Л5.8. Боевкин В.И., Айнутдинова И. Н., Кучминская А.И. Чувствительность динамических свойств линейной системы к изменению ее параметров. – Труды № 284. – М.: МВТУ, 1979. – 170 с.

Л5.9. Боевкин В.И. Моделирование при испытаниях автоматических информационных устройств. – М.: МВТУ, 1985. – 72 с.

Оглавление

Глава 5. Моделирование системы управления при лабораторных испытаниях (1)

Аннотация

5.1. Введение (3)

5.2. Цифровое моделирование непрерывныхдинамических систем

5.2.1 методы цифрового моделирования (3)

5.2.2. Численное решение линейных дифференциальных уравнений методом разложения в ряд Тейлора (4)

5. 2.3. Выражение ошибки численного решения через изменения коэффициентов дифференциального уравнения (6)

5.2.4. Выражение ошибки численного решения через изменение корней характеристического уравнения (8)

5.2.5. Устойчивость численного решения (10)

5.2.6. Повышение точности численного решения методом

коррекции уравнений движения (12)

5.3. Погрешности аналогового и полунатурного моделирования (14)

5.3.1. Особенности аналоговой вычислительной техники

5.3.2. Взаимосвязь приращений корней и коэффициентов

характеристического уравнения (15)

5.3.3. Влияние аналогового интегратора на корни

характеристического уравнения (17)

5.3.4. Погрешности полунатурного моделирования (21)

5.4 Упражнения Литература

Дата добавления: 2014-01-20