
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства интегрируемых функций
|
|
|
|
I.Если функция  интегрируема в
интегрируема в  , то и функция
, то и функция  и
и 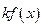 (где
(где  ) интегрируемы в
) интегрируемы в  .
.
Доказательство:
Проведём для функции  . Так как для любых двух точек
. Так как для любых двух точек 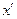 и
и 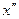 промежутка
промежутка  , имеем:
, имеем:  , то и колебание
, то и колебание  функции
функции  в этом промежутке не превосходит
в этом промежутке не превосходит 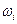 . Отсюда
. Отсюда
 ;
;
так как последняя сумма стремиться к нулю (при 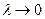 ), то первая и подавно, что влечёт интегрируемость функции
), то первая и подавно, что влечёт интегрируемость функции  .
.
Ч.т.д.
II.Если функции  и
и 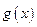 интегрируемы в
интегрируемы в  , то их сумма, разность и произведение также интегрируемы.
, то их сумма, разность и произведение также интегрируемы.
Доказательство:
Ограничимся случаем произведения  . Пусть
. Пусть 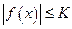 ,
, 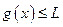 . Взяв в
. Взяв в  любые две точки
любые две точки 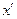 и
и 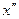 , рассмотрим разность:
, рассмотрим разность:
 ,
,
Где через 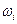 и
и 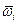 обозначены колебания функций
обозначены колебания функций  и
и 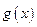 в
в  .
.
Но тогда для колебания 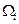 функции
функции  в
в  будем иметь:
будем иметь:  , откуда:
, откуда: 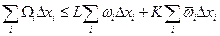 . Так как две последние суммы стремятся к нулю при
. Так как две последние суммы стремятся к нулю при 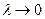 , то первая и подавно, что и доказывает интегрируемость функции
, то первая и подавно, что и доказывает интегрируемость функции  .
.
Ч.т.д.
III.Если функция  интегрируема в
интегрируема в  , то она интегрируема и в любой части
, то она интегрируема и в любой части  . Наоборот, если
. Наоборот, если  разложен на части, и в каждой части в отдельности функция
разложен на части, и в каждой части в отдельности функция  интегрируема, то она интегрируема и во всём промежутке
интегрируема, то она интегрируема и во всём промежутке  .
.
Доказательство:
Предположим, что функция  интегрируема в
интегрируема в  , и постоим для этого промежутка сумму
, и постоим для этого промежутка сумму 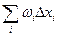 , считая, что
, считая, что 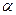 и
и 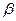 входят в состав точек деления. Аналогичная сумма для
входят в состав точек деления. Аналогичная сумма для 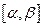 получиться отсюда, если опустить ряд (положительных) слагаемых; она наверно стремится к нулю, если стремится к нулю первая сумма.
получиться отсюда, если опустить ряд (положительных) слагаемых; она наверно стремится к нулю, если стремится к нулю первая сумма.
Пусть теперь  разложен, скажем, на две части
разложен, скажем, на две части  и
и  ,
, 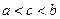 , и в каждой из них функция
, и в каждой из них функция  интегрируема. Возьмём снова сумму
интегрируема. Возьмём снова сумму 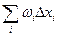 для
для  ; если точка
; если точка  оказалась в числе точек деления, то названная сумма составится из двух подобных же сумм для
оказалась в числе точек деления, то названная сумма составится из двух подобных же сумм для  и
и  и вместе с ними стремится к нулю.
и вместе с ними стремится к нулю.
Заключение. Это остаётся в силе и для случая, когда точка  не является точкой деления; присоединив эту точку, мы изменим лишь один член суммы, который сам, очевидно, стремится к нулю.
не является точкой деления; присоединив эту точку, мы изменим лишь один член суммы, который сам, очевидно, стремится к нулю.
|
|
|
Ч.т.д.
IV.Если изменить значения интегрируемой функции в конечном числе точек равных  , то интегрируемость её не нарушится.
, то интегрируемость её не нарушится.
Доказательство очевидно, ибо упомянутые изменения коснутся не более, чем  членов суммы
членов суммы 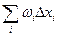 .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1663; Нарушение авторских прав?; Мы поможем в написании вашей работы!