
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства, выражаемые равенствами
|
|
|
|
I.Пусть  интегрируема в наибольшем из промежутков
интегрируема в наибольшем из промежутков 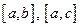 и
и  . Тогда она интегрируема в двух других, и имеет место равенство:
. Тогда она интегрируема в двух других, и имеет место равенство:
 ,
,
каково бы ни было взаимное расположение точек a,b и c.
Доказательство:
Положим сначала, что 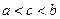 и функция интегрируема в
и функция интегрируема в  . То, что функция интегрируема в
. То, что функция интегрируема в  и
и  следует из III интегрируемых функций.
следует из III интегрируемых функций.
Рассмотрим разбиение  на части, причём точку
на части, причём точку  будем считать одной из точек деления. Составим интегральную сумму, будем иметь (смысл обозначений ясен):
будем считать одной из точек деления. Составим интегральную сумму, будем иметь (смысл обозначений ясен): 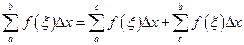 .
.
Переходя к пределу при 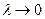 , мы получим требуемое равенство.
, мы получим требуемое равенство.
Пусть, например,  и функция
и функция  интегрируема в
интегрируема в  . Тогда, по доказанному, будем иметь:
. Тогда, по доказанному, будем иметь:

 .
.
II.Если  интегрируема в
интегрируема в  , то и
, то и 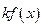 (где
(где  ) также интегрируема в этом промежутке, причём
) также интегрируема в этом промежутке, причём
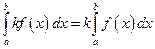 .
.
III.Если  и
и 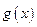 - обе интегрируемы в
- обе интегрируемы в  , то и
, то и 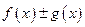 также интегрируема в
также интегрируема в  , причём
, причём
 .
.
В обоих случаях доказательство строится аналогично, исходя из интегральных сумм и переходя к пределу. Проведём его, например, для утверждения III.
Разобьём  произвольно на части и составим интегральную сумму для всех трёх интегралов. При этом точку
произвольно на части и составим интегральную сумму для всех трёх интегралов. При этом точку 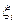 в каждом частичном промежутке выбираем произвольно, но для всех сумм одни и те же; тогда будем иметь
в каждом частичном промежутке выбираем произвольно, но для всех сумм одни и те же; тогда будем иметь  .
.
Пусть теперь 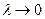 ; так как для обеих сумм справа пределы существуют, то существует и предел и для сумм слева, чем устанавливается интегрируемость функции
; так как для обеих сумм справа пределы существуют, то существует и предел и для сумм слева, чем устанавливается интегрируемость функции 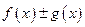 . Переходя в предыдущем равенстве к пределам, приходим к требуемому соотношению.
. Переходя в предыдущем равенстве к пределам, приходим к требуемому соотношению.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 339; Нарушение авторских прав?; Мы поможем в написании вашей работы!