Основная формула интегрального исчисления

.

Доказательство:

Можно применить свойство V к функция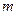м , и или непосредственно воспользоваться очевидными неравенствами:

, (*)

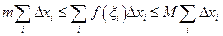(*) Так как , то все .

Доказанным соотношением можно создать более удобную форму равенства, освобождаясь в то же время от ограничения .

Теорема о среднем значении. Пусть интегрируема в , () и пусть во всём этом промежутке ; тогда

,

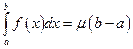где .

Доказательство:

Если , то по свойству VIII будем иметь

. Положив , получаем требуемое равенство. Для случая, когда 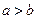, проводим то же рассуждение для , а затем, переставив пределы, приходим к прежней формуле.

Ч.т.д.

При дополнительном предположении о непрерывности на можно утверждать, что на этом промежутке найдётся точка такая, что

Обобщённая теорема о среднем значении. Пусть:

1)и и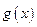нтегрируемы в ;

2);

3)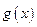во всём промежутке не меняет знака: .

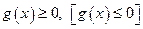Тогда

,

где .

Доказательство:

Пусть сначалаи ; тогда имеем

.

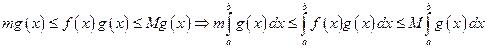В силу предположения о функции 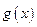имеем .

Если этот интеграл равен нулю, то из предыдущих неравенств ясно, что одновременно также , и утверждение теоремы становиться очевидным.

Если же интеграл больше нуля, то, разделив на него все части полученного выше двойного неравенства, положим

и придём к требуемому результату.

От случая легко можно перейти к случаю 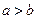, равно как от предположения - к предположению : перестановка пределов или изменение знака 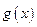не нарушает равенства.

Если непрерывна, то эта формула может быть записана следующем образом:

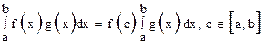
Определённый интеграл как функция верхнего предела.

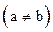Если функция интегрируема в , , то они интегрируемы в , где x – любое значение из . Заменив предел “b” определённого интеграла переменной x, получим выражение: 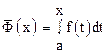, (7)

которое, очевидно, является функцией от x. Эта функция обладает следующими свойствами:

I.Если интегрируема в , то будет непрерывной функцией от .

Доказательство:

Придав x произвольное приращение (с тем, чтобы 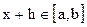), получим новое значение функции (7) ,

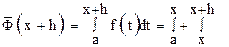так что .

Применим к этому интегралу теорему о среднем значении

, (8)

Здесь 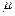содержится между точными границами 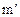и функции в , а следовательно, и подавно между (постоянными) границами её m и M в основном промежутке . Если устремить теперь h к нулю, то, очевидно, или 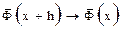, что и доказывает непрерывность функции .

II.Если функцию предположить непрерывной в точке t=x, то в этой точке функция имеет производную, равную , .

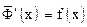Доказательство:

Действительно, из (8) имеем 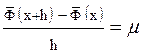, где .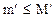

Но, ввиду непрерывности функции в точке t=x, по любому 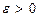найдётся такое , что при 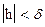, для всех значений t в промежутке , так что

.

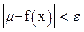Теперь ясно, что

.

Ч.т.д.

Мы пришли к заключению, имеющему огромное принципиальное и прикладное значение. Если предположить функцию непрерывной во всём промежутке , то она интегрируема и предыдущее утверждение оказывается приложим любой точке x этого промежутка: производная от интеграла (7) по переменному верхнему пределу x везде равна значению подынтегральной функции на этом пределе. Иными словами, для непрерывной в функции всегда существует первообразная; примером её является определённый интеграл (Ф) с переменным верхним пределом.

Для непрерывной в функции интеграл 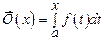является первообразной функцией. Если F(x)есть любая первообразная для , то

.

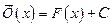Постоянную С легко определить, положив здесь x=a, ибо 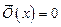; будем иметь:

.

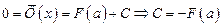Окончательно

.

В частности, при x=b получим

, (A)

Это – основная формула интегрального исчисления или формула Ньютона-Лейбница.

Если применить к интегралу теорему о среднем и вспомнить, что 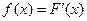, то получим

, ;

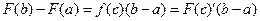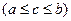Здесь легко узнается формула Лагранжа для функции F(x). Таким образом, с помощью основной формулы (А) устанавливается связь между теоремами о среднем в дифференциальном и интегральном исчислении.

Формула (А) даст эффективное и простое средство для вычисления определенного интеграла от непрерывной функции f(x).

Приведем примеры использования формулы (А). Заметим, что разность справа в формуле (А) обычно изображают символом «двойной подстановки от a до b» и формулу пишут в виде

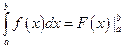, (А*)

Примеры:

1)

2), (a>0,b>0)

И другие.

Дата добавления: 2014-01-20