Интегрирование некоторых тригонометрических функций

1. Интегралы вида 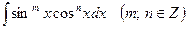можно свести к табличным, применяя:

а) формулы понижения степени

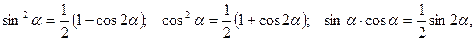
в случае, есл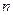и и неотрицательные четные числа.

Пример. Вычислить интеграл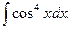

Решение. Здесь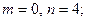

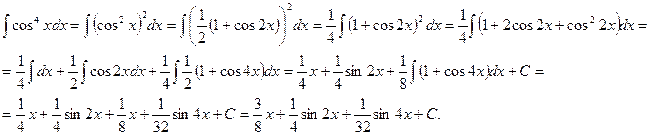б) подстановку 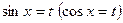, ес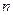ли или нечетные числа.

Допустим, для определенности, что 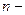нечетное 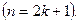Тогда,

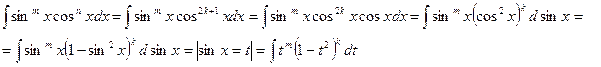
Полученный интеграл стал табличным.

Пример.. Вычислить интеграл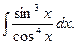

Решение. Здесь 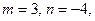и имеет место подстановка Тогда

2. Интегралы вида

С помощью замены переменной которая называется универсальной тригонометрической подстановкой, данный интеграл всегда сводиться к интегралу от рациональной функции. При такой замене имеем

Тогда,

Пример … Вычислить интеграл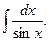

Решение. Произведем универсальную тригонометрическую подстановку. Получим

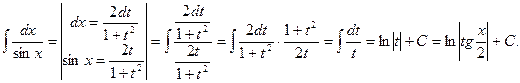
3. «Неберущиеся» интегралы

К настоящему времени разработано множество методов интегрирования. Мы рассмотрели лишь некоторые из них. Интеграл от элементарной функции который сам является элементарной функцией, называют «берущимся». Оказывается, что берущихся интегралов мало на фоне всех интегралов. Большинство интегралов являются «неберущимися», то есть не представимыми через элементарные функции, Так, например, нельзя взять интеграл 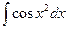, так как не существует элементарной функции, производная от которой была бы равна Приведем примеры «неберущих» интегралов:

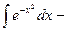интеграл Пуассона;

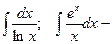интегральный логарифм и экспонента;

интегралы Френеля;

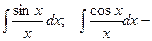интегральный синус и косинус;

Неберущиеся интегралы имеют богатую историю и многочисленные практические приложения. Интеграл Пуассона, например, описывает один из важнейших законов теории вероятности, а интегралы Френеля применяются в физике.

Дата добавления: 2014-01-20