Способ 2

Способ 1.

Представляем заданный интеграл в виде суммы двух интегралов по дугам 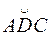и 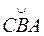и производим вычисления

Используя параметрические уравнения окружности: , , находим

Для вычисления интегралов по замкнутой кривой может быть полезна формула Грина, устанавливающая связь между криволинейным и двойным интегралами

,

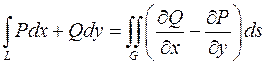где 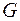– область, ограниченная кривой 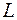; обход кривой 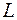производят таким образом, что область 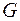остается слева.

Пример.

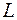Вычислить криволинейный интеграл по кривой , показанной на рис.18, пользуясь формулой Грина

.

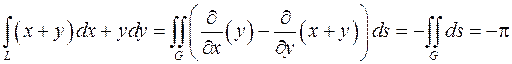Двойной интеграл от единицы равен площади области 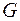, то есть площади круга.

Пример.

При помощи криволинейного интеграла вычислить площадь фигуры ограниченной эллипсом: , .

Запишем площадь фигуры через двойной интеграл и при помощи формулы Грина выразим его через криволинейный интеграл по эллипсу

.

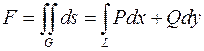При этом 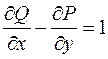. Примем , , тогда

.

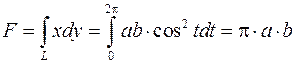В физических приложениях часто встречается криволинейный интеграл, подынтегральное выражение которого является полным дифференциалом некоторый функции , то есть

.

Условием полного дифференциала является равенство частных производных

.

Согласно формулы Грина отсюда следует равенство нулю криволинейного интеграла от полного дифференциала, взятого по любой замкнутой кривой. Это значит, что значение такого интеграла не зависит от пути интегрирования, соединяющего две заданные точки. Это свойство широко используется при вычислении интегралов.

Пример.

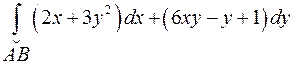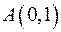Вычислить по дуге кривой , соединяющей точки и .

Вследствие равенства частных производных

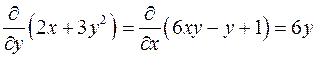
заключаем, что подынтегральное выражение является полным дифференциалом. Интеграл от полного дифференциала не зависит от пути интегрирования, поэтому в качестве такового можно взять любую удобную для нас кривую. Выбираем ломаную линию, состоящую из горизонтального отрезка 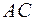, соединяющего точк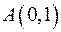и и 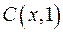, и вертикального отрезка .

Имеем

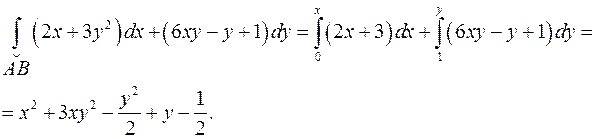
Принимая в качестве дуги интегрирования ломаную, соединяющую точк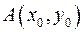и , и , выводится формула Ньютона-Лейбница

.

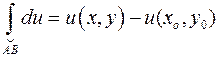Из формулы Ньютона-Лейбница следует способ нахождения функции по ее полному дифференциалу через криволинейный интеграл

.

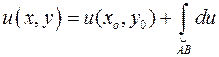Например, из рассмотренного примера находим

,

где 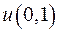– произвольная постоянная.

Дата добавления: 2014-01-20