Интегрирование по частям. Теорема.Пусть функции u(x) и v(x) дифференцируемы на множестве М и, кроме того, на этом множестве существует первообразная для функции

Теорема. Пусть функции u(x) и v(x) дифференцируемы на множестве М и, кроме того, на этом множестве существует первообразная для функции 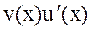. Тогда на множестве М существует первообразная для функции и справедлива формула

(1)

Замечание 1. В концевых точках множества М (если М - сегмент) рассматриваются односторонние производные.

Замечание 2. Определение дифференциала и свойство инвариантности его формы позволяют записать эту формулу в виде

Доказательство теоремы. Запишем формулу для производной произведения функций u(x) и v(x).

.

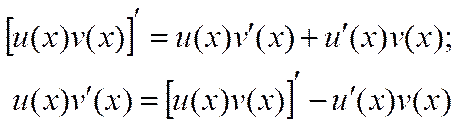Умножим последнее равенство на dx и возьмем интеграл от обеих частей полученного равенства. Так как по условию на М существует

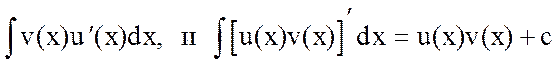, то на М существует

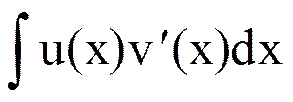и справедлива формула

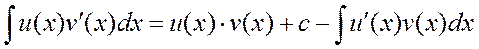
Включая произвольную постоянную С в 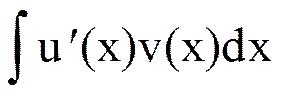, получим формулу (1).

Формула (1) сводит вопрос о вычислении интеграла 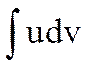к вычислению интеграла 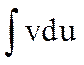. В ряде конкретных случаев этот последний интеграл проще исходного.

Вычисление интеграла 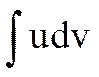посредством применения формулы (1) называют интегрированием по частям.

Примеры:

1⁰.

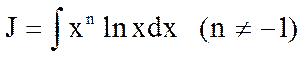
u=lnx, dv=xⁿdx;

2⁰.

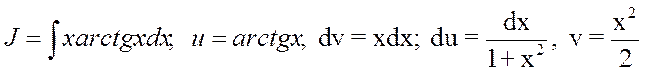
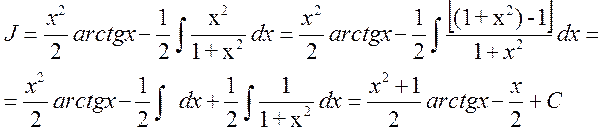
3⁰.

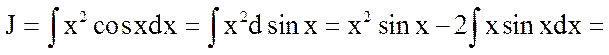
Еще раз применим формулу интегрирования по частям

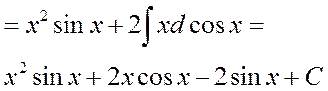
4⁰.

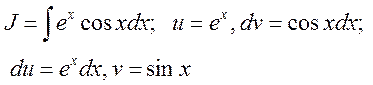
Еще раз применим формулу интегрирования по частям

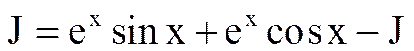
Это равенство понимается как равенство множеств (т.е. как равенство представителей множеств J и e^xsinx+e^xcosx-J) c точностью до произвольной постоянной, поэтому отсюда получаем

5⁰.

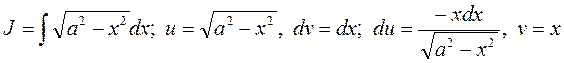
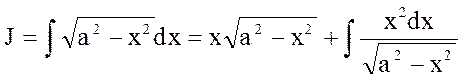
Добавим и вычтем а² в числителе подынтегральной функции интеграла, стоящего в правой части равенства; тогда, произведя деление на , будем иметь

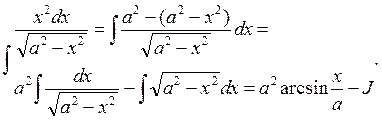Подставим это выражение в формулу (2), получим

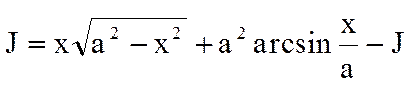
Отсюда

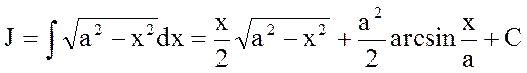
6⁰. Проводя аналогичные вычисления, легко получить, что

.

Теорема 3. Пусть 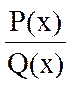- правильная рациональная дробь с вещественными коэффициентами, знаменатель которой имеет вид:

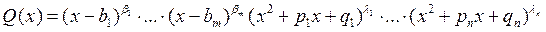
Тогда для этой дроби справедливо следующее разложение на сумму простейших дробей:

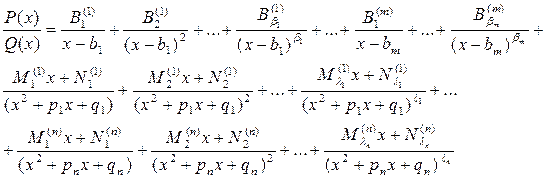(1)

В этом разложении - некоторые вещественные постоянные, часть которых может быть равна 0.

Замечание. Для определения постоянных в общем случае следует привести равенство (l) к общему знаменателю и после этого сравнить коэффициенты при одинаковых степенях в числителях. При этом, если степень многочлена Q(x) равна s, то вообще говоря, в числителе правой части равенства (1) после приведения к общему знаменателю получается многочлен степени s-1, т.е. многочлен с s коэффициентами, число же неизвестных также равняется s.

Таким образом, мы получаем систему s уравнений с s неизвестными. Существование у нее решения вытекает из доказательства теоремы.

Рассмотрим основные методы разложения на простейшие дроби.

Дата добавления: 2014-01-20