Высота гайки и глубина завинчивания

Равнопрочность резьбы и стержня винта является условием назначения высоты стандартных гаек. По тем же соображениям

 

устанавливают глубину завинчивания

винтов и шпилек в

детали.

Высоту нормальных стандартных гаек крепежных изделий принимают

H = 0,8 d.

Кроме нормальных, стандартом предусмотрены высокие H= 1,2 d и низкие H = 0,5 d гайки. Прочность резьбы при нормальных и высоких гайках превышает прочность стержня винта. То же имеем при стандартной глубине завинчивания: в стальные детали H1=d, в чугунные и силуминовые Н1= 1,5 d.

Стандартные высоты гаек (за исключением низких) и глубины

завинчивания исключают необходимость расчета на прочность резьбы стандартных крепежных деталей.

Расчет на прочность стержня винта (болта) при различных случаях нагружения

Рассмотрим четыре случая работы соединения.

1. Стержень винта нагружен только внешней растягивающей силой F.

2. Болт затянут, внешняя нагрузка отсутствует.

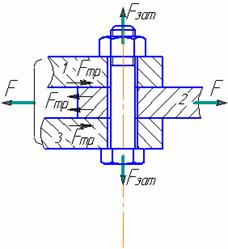
3. Болтовое соединение нагружено силами, сдвигающими детали в стыке.

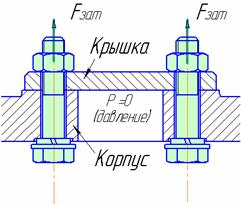
4. Болт затянут, внешняя нагрузка раскрывает стык деталей.

 

Первый случай. Примером служит резьбовой участок грузового болта для подвешивания груза. Опасным является сечение, ослабленное резьбой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d1 резьбы. Условие прочности по напряжениям растяжения в стержне

F

s =[(p)

2 ]£[ s ],

/ 4 d 1

где допускаемое напряжение для растягивающей внешней нагрузки без затяжки болтов [σ] = 0,6 σT.

 

Второй случай. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин. В этом случае стержень болта растягивается осевой силой Fзат, возникающей от затяжки болта, и закручивается моментом сил трения в резьбе Тр, т.е. работает на кручение. Прочность болта определяют по эквивалентному напряжению

sэкв =

s 2 + 3 t 2

£[ s ].

Для стандартных метрических резьб расчеты показывают, что σэкв»1,3 σ. Это позволяет производить расчет прочности болтов по упрощенной формуле

s = [(p

) 2 ]£

[ s ]

1, 3 × F зат

экв

/4 d 1.

В среднем и тяжелом машиностроении не рекомендуют применять болты малых диаметров (меньше М8), т.к. их можно разрушить при недостаточно квалифицированной затяжке.

 

Третий случай. Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах: первый, болт поставлен с зазором; второй – болт поставлен без зазора. Начнем рассмотрение с варианта, когда болт поставлен с зазором.

Внешняя нагрузка уравновешивается силами трения в стыке, которые образуются от затяжки болта. Без затяжки

болтов детали могут сдвигаться на

величину зазора, что недопустимо. Рассматривая равновесие детали 2, получаем условие отсутствия сдвига деталей

F £ i Fтр = i Fзат f, или Fзат=KF/(if),

где i – число плоскостей сдвига деталей (на рисунке i = 2); f – коэффициент трения в стыке; (f = 0,15…0,20); K – коэффициент запаса (K = 1,3…1,5 при статической нагрузке, K = 1,8…2 при переменной нагрузке).

Прочность болта оценивают по эквивалентному напряжению σэкв. Замечание: В соединении, в котором болт поставлен с зазором,

внешняя нагрузка не передается на болт. Поэтому болт

рассчитывают только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают путем выбора повышенных значений коэффициента запаса.

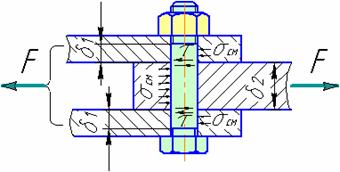
Болт поставлен без зазора.

 

В этом случае отверстие под болт калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности соединения не учитывают

силы трения в стыке, так как затяжка болта не обязательна. В общем

случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия.

Условие прочности по напряжениям среза

F

t =[(p / 4) d 2 i ]£

[ t ].

Расчет на смятие производится по условным напряжениям из-за сложности установить точный закон распределения напряжений по цилиндрической поверхности деталей. При этом для средней детали

[ s

(и при соединении только двух деталей)

Для крайних деталей

sсм

F

=

(d × d 2)

£ см ].

=

sсм

F

£

2 (d × d 1)

[ s см ].

Из двух значений σсм расчет прочности выполняют по наибольшему, а допускаемое напряжение определяют по более слабому материалу болта или детали.

Четвертый случай. Болт затянут, внешняя нагрузка

 

раскрывает стык деталей. Примером служат болты для крепления крышек цилиндров (резервуаров), нагруженных давлением р жидкости или газа.

Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой. Обозначим: Fзат – сила затяжки болта; F1 = F/z – внешняя нагрузка соединения (от давления), приходящаяся на один

болт; z – число болтов. Приложение внешней нагрузки вызывает дополнительную нагрузку на болт

Fd = c × F 1,

где χ – коэффициент внешней нагрузки, который определяется по условию равенства деформаций болта и деталей:

c = lд

l д

+ ld

где λδ – податливость болта, равная его удлинению при единичной нагрузке; λд – суммарная податливость соединяемых деталей. Расчетная (суммарная) нагрузка болта:

Fp = Fзат + χ F1.

Для большинства практических случаев расчет податливостей

деталей связан с большими трудностями. Между тем расчеты и испытания конструкций показывают, что χ можно принять равным или меньше (0,2….0,3) для соединений без мягких прокладок.

а) Прочность болта при статической нагрузке:

s = ()

£[ s ].

1,3 Fp

p × d 1

Здесь коэффициент 1,3 по-прежнему учитывает напряжения кручения, которые могут возникнуть при затяжке соединения под нагрузкой.

б) Прочность болта при переменных нагрузках.

=[ F

При переменных нагрузках полное напряжение в болте можно разделить на постоянное (σm) и переменное с амплитудой (σа):

sm зат

+(Fd

/ 2)]/ Ad;

sa =(Fd

/ 2)/ Ad.

Запас прочности по переменным напряжениям подсчитывают по формуле:

s =

s -1

sa × Ks + ys × sm,

где σ-1– предел выносливости материала болта; Kσ – эффективный

коэффициент концентрации напряжений в резьбе; ψ σ

»0,1–

коэффициент чувствительности к асимметрии цикла напряжений.

Переменные напряжения вызывают явление усталости. Чем меньше χ, тем выше сопротивление болта усталости. При этом, упругие болты – хорошая защита от усталостного разрушения.

ЛЕКЦИЯ №26

Дата добавления: 2014-01-20