Приклад. Теорема 11. Якщо функції та мають неперервні похідні для , то

Теорема 11. Якщо функції та мають неперервні похідні для, то

(7.14)

Формули наближеного обчислення
визначених інтегралів

Визначений інтеграл від заданої неперервної функції далеко не завжди можна легко та точно обчислити. Однак, використовуючи геометричний зміст, можна побудувати ряд наближених формул, за допомогою яких інтеграл обчислюється з будь-якою точністю. Розглянемо такі формули.

Нехай від заданої та неперервної на 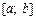функції треба обчислити визначений інтеграл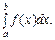

Поділимо 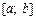точками а = х ₀, х ₁, х ₂,..., х_{n –1}, x_n = b на n рівних частин завдовжки .

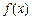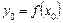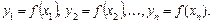Значення функції у точках позначимо так: , Побудуємо для функції на проміжку 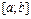інтегральні суми, кожна з яких буде наближено подавати визначений інтеграл:

(7.15)

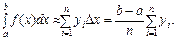(7.16)

Формули (7.15) та (7.16) називаються формулами лівого та правого прямокутників відповідно. Ця назва пов’язана з тим, що криволінійна трапеція наближено замінюється відповідною ступінчастою фігурою (рис. 7.8).

Рис. 7.8

ІІ. Формула трапецій.

Більш точне значення визначеного інтеграла буде, якщо криву замінювати не ступінчастою лінією, а вписаною ламаною, тобто криволінійна трапеція замінюється сумою n прямолінійних трапецій (рис. 7.9). У цьому разі наближене значення інтеграла можна дістати як середнє арифметичне значень, обчислених за формулами (7.15) та (7.16).

(7.17)

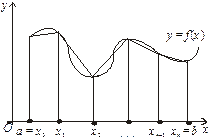
Рис. 7.9

ІІІ. Формула Сімпсона.

Поділимо 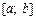на парне число рівних частин точками 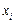так, що а = х ₀, b = x _{2 m} . На кожному із цих проміжків криволінійну сторону трапеції, рівнянням якої є ,

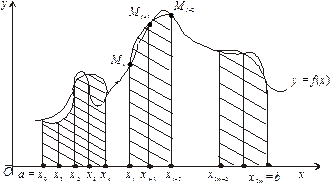
Рис. 7.10

замінюємо певною параболою. Таке наближення для обчислення визначеного інтеграла буде точнішим, ніж за попередніми формулами (рис. 7.10).

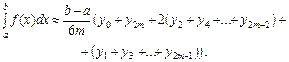(7.18)

Обчислення площ плоских фігур
в прямокутній системі координат

Якою б не була криволінійна фігура, що обмежена неперервними кривими лініями, шляхом її розсікання лініями паралельними осям координат, обчислення площі фігури можна звести до обчислення площ розглянутих нижче фігур.

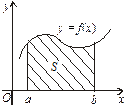
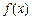І. Фігура обмежена лініями , y = 0, x = a, x = b (рис. 7.11). Функція — неперервна та Площа S такої криволінійної трапеції за геометричним змістом визначеного інтеграла така: .

Якщо при виконанні всіх інших умов 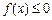(рис. 7.12),

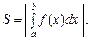(7.20)

Рис. 7.11	Рис. 7.12	Рис. 7.13

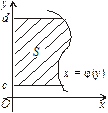
ІІ. Фігура обмежена лініями 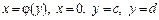(рис. 7.13). Функція 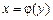— неперервна та 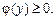Площа S такої фігури буде

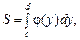(7.21)

а якщо (рис. 7.14), то

(7.22)

ІІІ. Фігура обмежена лініями , 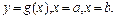Функ­ції та 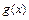— неперервні та 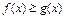для 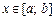(рис. 7.15). Площа S такої фігури визначається як різниця площ фігур аА ₂ В ₁ b та аА ₂ В ₁ b

(7.23)

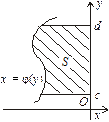
Рис. 7.14 Рис. 7.15

Приклад. Обчислити площу фігури, обмеженої лініями

та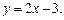

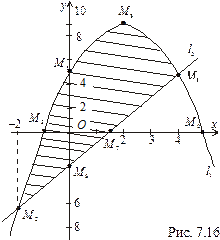
Побудуємо фігуру, обмежену параболою 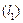та прямою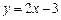 на координатній площині; при цьому знаходимо точки перетину заданих ліній між собою та з осями координат, а також координати вершини параболи (рис. 7.16).

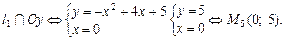
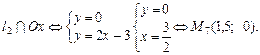
Точка 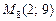— вершина параболи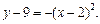

Площа S фігури M ₁ М ₈ М ₂ за формулою (7.23) буде така:

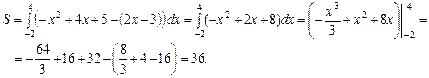
Обчислення об’єму тіла

Задача. Знаючи закон зміни площі поперечного перерізу тіла, знайти його об’єм.

Розв’язання. Нехай функція — площа поперечного перерізу тіла площиною, перпендикулярною до осі Ох у деякій точці 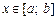. Відрізок 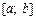дає лінійний розмір тіла в напрямі осі Ох.

Поділимо проміжок 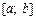на n частин точками так, що 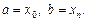Через ці точки проведемо площини перпендикулярно до осі, у результаті чого тіло буде розбито на n частин. Кожну з цих частин наближено замінимо циліндром з висотою та площею основи , де (рис. 7.17).

Рис. 7.17

Тоді об’єм тіла наближено дорівнюватиме інтегральній сумі 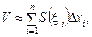а точне значення об’єму тіла подаватиметься границею

(7.24)

якщо ця границя існує за (7.8).

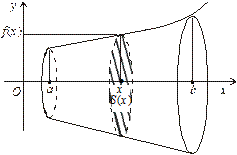
Задача. Знайти об’єм тіла 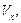утвореного обертанням навколо осі 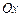фігури, обмеженої лініями (рис. 7.18).

Розглядаючи цю задачу, як частинний випадок попередньої задачі, встановлюємо, що площа поперечного перерізу 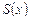в даному випадку є площа круга радіусом , тобто 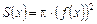, а об’єм тіла обертання за формулою (7.24) буде таким:

(7.25)

Рис. 7.18	Рис. 7.19

Зауваження. Аналогічно, об’єм тіла 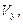утвореного обертанням навколо осі Оу фігури, обмеженої лініями х = 0, , , 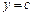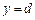(див. рис. 7.13), матиме вигляд

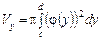. (7.26)

Приклад. Обчислити об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої лініями 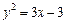, х = 1, х = 4.

l У прямокутній системі координат будуємо фігуру, обмежену даними лініями (рис. 7.19). За формулою (7.25) об’єм тіла буде таким: .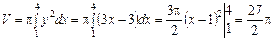

Дата добавления: 2014-01-11