Система нормативного регулирования бухгалтерского учета и отчетности в России

Юча

х_вх х_вих

W(p) = k(τp+1) х_вих = k(τ dх_вх/dt+ х_вх)

Контрольні запитання до лекції 2.

1. Наведіть основні визначення і поняття теорії автоматичного управління; об'єкт управління, вхідні і вихідні впливи.

2. Що розуміється під зміст задач управління динамічними об'єктами?

3. Визначення і склад САУ. Що таке функціональна схема САУ?

4. Стисла характеристика фізичних елементів САУ: об'єкти управління, датчики, підсилювальні і виконавчі елементи, що корегують прилади, елементи порівняння, вхідні і вихідні змінні.

5. Як розрізняються головні і місцеві зворотні зв'язки, жорсткі і гнучкі зворотні зв'язки?

6. Які ви знаєте принципи і закони регулювання?

7. Що таке статичний режими роботи САУ?

8. Основні визначення статики САУ, статична помилка регулювання.

9. Динамічні режими роботи САУ.

10. Які ви знаєте основні показники динамічних режимів роботи систем автоматичного управління?

11. Математичний опис динаміки елементів САУ.

12. Визначення поняття передадаточних функцій.

13. Які ви знаєте передаточні функції елементів, і систем автоматичного управління?

14. Охарактеризуйте типові структурні ланки лінійних САУ.

15. Чим відрізняються передаточні і перехідні функції типових структурних ланок?

16. Як ви розумієте передаточні функції сполучень ланок: послідовного, паралельного, охоплених зворотними зв'язками; загальний випадок сполучення ланок; розімкнені САУ з перехресними зворотними зв'язками?

17. Передаточні функції замкнутих САУ за керуючим і збурюючим впливами.

18. Визначення і призначення частотних характеристик елементів і систем автоматичного управління.

Лекція 3. Стійкість лінійних динамічних систем

Найважливішою задачею аналізу динамічних систем є розв’язання питання про їх стійкість, тобто наявності чи відсутності в системі здатності вертатися до рівноважного стану, з якого вона виводиться обурюючими чи, оскільки будь-який вплив на таку систему викликає неприпустиме зростання фізичних величин, які характеризують роботу системи (струм, електрична напруга, прискорення, механічна напруга, тощо).

Виникнення управляючими впливами. Раніше помічалося, що нестійка система непрацездатнанестійких (розбіжних) коливань у системі можна пояснити, наприклад, прослідкувавши включення системи управління величиною х_вих.. Управляюча величина на вході регулятора х_р в режимі встановленої роботи системи визначається як різниця х_р=х_вх–х_зз. В перший момент включення системи в силу інерційності зворотнього зв’язку(ЗЗ) х_зз=0, отже, х_р=х_вх, тобто х_р>>х_{р.вст .}, де: х_р.вст. – управляючий вплив на вході регулятора. Дійсно, це може викликати значне зростання вихідної величини х_вих››х_{вих.вст .}, яка буде зростати доти, доки сигнал зворотного зв’язку не зменьшить значення х_р. Однак, величина х_вих., яка значно зросла, через ЗЗ передається на вхід системи та суттєво зменшить значення х_р, що може призвести до наступного зниження величини х_{вих .} та виникнення умови х_вих << х_{вих.вст .}. При несприятливому співвідношенні параметрів системи описанні коливальні процеси можуть стати розбіжними.

Задача дослідження систем на стійкість може бути поставлена подвіййно: 1) чи стійка система при заданому значенні її параметрів; 2) в яких діапазонах можна змінювати параметри системи, не порушуючи її стійкості. Друга постановка задачі про стійкість має місце при налагодженні та експлуатації системи автоматичного управління.

Аналіз системи на стійкість та вибір засобів для стабілізації нестійких систем здійснюється із застосуванням критеріїв (ознак) стійкості, які формулюються виходячи із загальних умов стійкості.

Питання про стійкість системи зводиться до з’ясування стійкості вільного руху системи та вимагає аналізу характеру розв’язання рівняння вільного руху, складеного відносно відхилення вихідної величини х від стану,який встановився. На основі диференційного рівняння вільного руху в розімкненій лінійній динамічній системі та операторного рівняння вільного руху в замкненій системі рівняння вільного руху системи може бути приведене до виду:

a₀ dⁿx/dtⁿ + a₁ d^n-1x/dt^n-1 + … + a_n-1 dx/dt + a_nx = 0, (3.1)

де: n – порядок рівняння системи; a_i – коефіцієнти, які визначаються з параметрів системи.

Лінійне однорідне диференційне рівняння (3.1) має загальний розв’язок виду:

x = c₁e^p1t + c₂e^p2t + … + c_ne^pnt, (3.2)

де: с₁, с_i, с_n – постійні інтегрування; р₁, р_i, р_n – корені характеристичного рівняння.

Характеристичне рівняння, яке відповідає диференційному рівнянню (3.1), має вигляд: К(р) + Н(р) = 0, де К(р), Н(р) – характеристичні поліноми, відповідно, чисельника і знаменника передаточної функції розімкненої системи.

Якщо аналізується стійкість розімкненої системи, то як слідує з (2.29), характеристичне рівняння має вигляд: Н(р) = 0. Частіше необхідно аналізувати стійкість замкненої системи.

У всіх випадках характеристичне рівняння вільного руху приводиться до виду:

a₀ pⁿ + a₁ p^n-1 + … + a_i p^n-i + … + a_n-1 p + a_n = 0. (3.3)

Корені рівняння (3.3) можуть бути або дійсними, або комплексними попарно спряженими.

У випадку дійсних коренів позначимо р_i=λ_i. Тоді загальний розв’язок рівняння (3.1) представляється як сума n розв’язків виду: х_i=с_ie^λit. Так як в (3.1) величина х означає відхилення регульованої величини від стану, який встановився, то очевидна умова стійкості при t > 0 має вигляд: x(t)>0. Кожна складова загального розв’язку прямує до нуля лише при від’ємному значенні дійсного кореня, тобто при t_i < 0.

Комплексні корені мають вигляд: p_k = α_k ± jω_k, де: α_k – дійсна частина комплексного кореня; ± jωk- коефіцієнт при уявній частині – кутова частота коливань.

Кожному кореню р_k у випадку, який розглядається, буде відповідати частковий розв’язок:

x_k = X_k sin (ω_kt + φ_k), (3.4)

де: Х_k = B_k e^αkt – амплітуда складової х_k; B_k, φ_k – постійна інтегрування.

Рух, що описується рівнянням (3.4), буде збіжним, якщо при t®¥ рішення x_k(t)®0. Це можливо лише при від’ємному значенні дійсної частини комплексного кореня.

Виходячи з викладеного, можна вивести умову стійкості лінійних динамічних систем: лінійна система буде стійкою, якщо всі дійсні корені і всі дійсні частини комплексних кореней характеристичного рівняння, яке відповідає початковому диференційному равнянню вільного руху системи, будуть від’ємні.

Дуже важливою для практичного аналізу стійкості є геометрична інтерпретація умов стійкості. Вона зводиться до того, що в стійкій лінійній системі всі корені характеристичного рівняння, яке відповідає диференційному равнянню вільного руху системи, на комплексній площині в координатах a-jw розташовуватися зліва від уявної осі. Такі корені будемо називати “лівими”. Отже умова стійкості в такій постановці зводиться до того, щоб корені характеристичного рівняння були лише “лівими”. Виходячи з цього, в теорії управління розроблений ряд ознак – критеріїв стійкості лінійних динамічних систем, які дозволяють винести судження про стійкість системи, не обчислюючи значення коренів характеристичного рівняння. В практиці дослідження лінійних систем автоматичного управління широко використовуються дві групи критеріїв стійкості – алгебраїчні та частотні. Застосування того чи іншого критерію визначається умовою конкретної задачі, наприклад порядком диференційного рівняння вільного руху системи, наявністю чи відсутністю тих чи інших характеристик системи, яка досліджується – передаточних функцій, АФХ, ЛАФЧХ та інших.

Не зупиняючись на доведеннях, які побудовані на твердженні необхідності лівих коренів для забезпечення стійкості лінійної динамічної системи, наведемо деякі з критеріїв стійкості.

Критерій Рауса. Практичне використання алгебраїчного критерія Рауса зводиться до того, що на базі значень коефіцієнтів характеристичного рівняння (3.3) складається таблиця Рауса, коефіцієнти якої b_re назвемо елементами таблиці Рауса, де r – номер рядка таблиці, e – номер стовпчика.

Елементи першого рядка таблиці є коефіцієнтами характеристичного рівняння (3.3) з парними індексами, тобто b₁₁ = a₀, b₁₂ = a₂ і т. д. Елементи другого рядка представляють собою коефіцієнти рівняння (3.3) з непарними індексами, тобто b₂₁ = a₁, b₂₂ = a₃ і т.д. Для знаходження інших елементів таблиці Рауса можна скористатися виразом:

b_re =(b_r-1,1 b_r-2,e+1 – b_r-2,1 b_r-1,e+1 ) / b_r-1,1.

b11	b12	b13	b14	…	…	…
b21	b22	b23	b24	…	…	…
b31	b32	b33	b34	…	…	…
...	...	....	....	...	...	...
...	...	....	....	...	...	...

Критерій Рауса формулюється так: лінійна динамічна система буде стійкою, якщо всі елементи першого стовпчика таблиці Рауса додатні. Форма критерія Рауса дозволяє легко реалізувати його за допомогою ЕОМ.

Критерій Гурвіца.

Для аналізу стійкості лінійної системи по критерію Гурвіца з коефіцієнтів характеристичного рівняння (3.3) складаємо визначники Гурвіца:

а₁ а₀ 0 0

а₁ а₀ а₁ а₀ 0 а₃ а₂ а₁ 0

D₁ = а₁; D₂ = а₃ а₂; D₃ = а₃ а₂ а₁; D₄ = а₅ а₄ а₃ а₂ .

а₅ а₄ а₃ а₇ а₆ а₅ а₄

Кількість визначників Гурвіца дорівнює порядку характеристичного рівняння n.

За критерієм Гурвіца - лінійна динамічна система буде стійкою, якщо всі коефіцієнти характеристичного рівняння та всі визначники Гурвіца додатні.

Будь-який визначник D_i складається за одним загальним правилом: кількість рядків та стовпчиків визначника D_i дорівнює i; по діагоналі визначника розташовуються підряд коефіцієнти характеристичного рівняння від а₁ до a_i; вліво від діагоналей на кожному рядку розташовуються коефіцієнти із зростаючими індексами, вправо – зі спадаючими. Елементи, які розташовуються вправо від а₀, та елементи з індексами, що перевищують ступінь характеристичного рівняння, заміняються нулями.

З критерія Гурвіца випливають прості алгебраїчні вирази, складені з коефіцієнтів характеристичного рівняння, зручні для аналізу стійкості систем невисокого порядку. Так, для системи першого та другого порядків достатньою умовою стійкості є додатність всіх коефіцієнтів характеристичного рівняння. Для систем більш високого порядку ці умови зберігаються, але, крім того, необхідне виконання наступних співвідношень:

- в системах третього порядку а₁а₂ - а₀а₃ > 0;

- в системах четвертого порядку (а₁а₂ – а₀а₃)а₃ – а₁² а₄ > 0.

Недолік критерія Гурвіца – громіздкість обчислень визначника для систем високого порядку.

Частотний критерій стійкості – критерій Михайлова.

Частотні критерії базуються на властивостях частотних характеристик стійких систем. Велику роль в розвитку теорії стійкості зіграв частотний критерій стійкості, запропонований в 1936 р. А.В. Михайловим. Так, як і алгебраїчні критерії, частотні критерії витікають з обов’язкової умови наявності лише лівих коренів в характеристичному рівнянні стійкої лінійної динамічної системи. Не зупиняючись на доведеннях критерію А.В. Михайлова, розглянемо його практичне використання для аналізу стійкості. З цією ціллю характеристичне рівняннязапишемо у вигляді

a₀pⁿ + a₁pⁿ⁺¹ + … + a_n-1p + a_n = F(p). (3.5)

Поклавши в (3.5) p = jp = jw і відокремлюючи дійсну частину від уявної, поліном F(p) приведемо до виду:

F(jw) = U(w) + j V(w), (3.6)

де: U(w) - дійсна частина – сума всіх членів, які містять j в парних ступенях; V – уявна частина виразу.

У відповідності з критерієм Михайлова умова стійкості:

D arg F(jw) = n (p/2), 0 < w < ¥. (3.7)

Геометричне місце точок кінця вектора F(jω) при зміні частоти в діапазоні 0<w<¥ називається годографом вектора, або годографом Михайлова. У відповідності з (3.7) критерій Михайлова формулюється наступним чином: динамічна система, яка описується лінійним диференційним рівнянням n-го порядка, стійка, якщо при зміні w від 0 до ¥ годограф вектора F(jw) послідовно проходить в додатньому напрямку (проти годинникової стрілки) n квадрантів комплексної площини.

V(w) V(w) V(w)

n=2 n=4 n=6

U(w) U(w) U(w)

Рис. 3.1 Годографи стійких систем

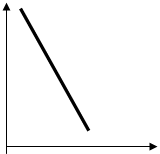V(w) V(w) V(w)

n=2 n=4 n=6

U(w) U(w) U(w)

Рис. 3.2 Годографи нестійких систем

АФХ замкнутої системи описується виразом:

W_з(jω) = W_р(jω) / [1 + W_р(jω)]. (3.8)

Позначимо знаменник отриманого виразу через W₁(jω).

W₁(jω)=1+W_р(jω)=1+ К_р(jω)/Н_р(jω) = Н(jω)/Н_р(jω), (3.9)

де Н(jω)=К_р(jω)+Н_р(jω) – характеристичний поліном замкненої системи при р= jω.

У відповідності з властивостями передаточних функцій порядок полінома Н(р) не перевищує порядка полінома Н_р(jω), так як Н(р) = К(р) + Н(р), а порядок полінома К_р(р) меньше порядка полінома Н_р(р).

Тому критерій Михайлова для замкненої системи можна записати у вигляді:

Δarg Н(jω) = (n – 2m) π/2, 0 < ω < ∞, (3.10)

де: m – число правих коренів системи, яка в замкненому стані має характеристичний поліном Н(р) = 0.

Коефіцієнт 2 перед m введений тому, що кожний правий корінь не тільки не забезпечує додатнього повороту вектора, але й створює його від’ємний поворот (за годинниковою стрілкою).

З (3.9) витікає, що arg W₁(jω) = arg H(jω) - arg H_p(jω).

Або, врахувавши (3.8) та (3.10), отримуємо:

arg W₁(jω) = (n – 2m) π/2 - n π/2 = -m π.

В стійкій замкненій системі правих коренів в характеристичному рівнянні немає, тобто m = 0, отже,умовою стійкості замкненої системи буде:

arg W₁(jω) = 0. (3.11)

Q(ω) Q(ω)

φ₁(ω) ω=0

P(ω) P(ω) W₁(jω)

а б

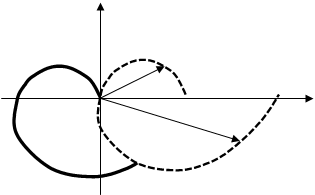
Рис. 3.3 Амплітудно-фазовий критерій стійкості (критерій Найквіста): а – окремий випадок; б – загальний.

Умова (3.11) виконується тільки тоді, коли крива W₁(jω) при зміні частоти від 0 до ∞ не охоплює початку координат на комплексній площині Р(ω); jQ(ω), де Р(ω) – дійсна частина виразу W₁(jω), Q(ω)- уявна частина (рис.3.3).

Як видно з (3.9), перехід на комплексній площині від годографа вектора W₁(jω) до годографа вектора АФХ розімкненої системи W_р(jω) здійснюється зсувом кривої W₁(jω) вліво на -1, так як W_р(jω) = W₁(jω) – 1.

Виконавши цю операцію, отримуємо наступне формулювання амплітудно-фазового критерія стійкості – критерія Найквіста: лінійна динамічна система, стійка в розімкненому стані, стійка і в замкненому стані, якщо АФХ розімкненої системи при зміні частоти від 0 до ∞ не охоплює на комплексній площині точку з координатами (-1;j0) (рис. 3.3 а)).

Більш загальне формулювання критерію Найквіста відноситься до систем, які мають так звану АФХ другого роду (рис. 3.3 б)), коли W_р(jω) декілька разів перетинає дійсну вісь зліва від точки Р(ω)=1. Додатнім будемо вважати перехід годографа через дійсну вісь, якщо він здійснюється знизу вгору. Тоді формулювання критерію Найквіста приймає вигляд: лінійна динамічна система, стійка в розімкненому стані, стійка і в замкненому стані, якщо при зміні частоти від 0 до + ∞ різниця між числом додатніх переходів годографа АФХ розімкненої системи через ділянку дійсної осі (-1, 0) та числом від’ємних переходів рівна нулю. З цієї умови видно, що система, стійка в розімкненому стані і яка має АФХ в формі кривої, показаної на рис.3.3 б), стійка і в замкненому стані.

Q(ω)

В

-1

Р(ω)

А

3 2 1 а

L,φ 1 L,φ 2 L,φ 3

L(ω) L(ω) L(ω)

Ω ω ω φ(ω) φ(ω) φ(ω)

б в г

Рис 3.4. Логарифмічний критерій стійкості

Логарифмічний критерій стійкості.

Цей критерій заснований на зв’язку властивостей стійкої замкненої динамічної системи з формою ЛАФЧХ розімкненої системи (рис3.4).

У відповідності з критерієм Найквіста стійка розімкнена система, яка має АФХу формі кривої 1, стійка з запасом по фазі, що дорівнює α. При цьому під запасом по фазі розуміється кут між від’ємними напрямами дійсної осі й прямої, яка з’єднує початок координат з точкою А – точкою перетину АФХ розімкненої системи з окружністю одиничного радіуса.

Система, яка має в розімкненому стані АФХ в формі кривої 2, будучи стійкою в розімкненому стані, в замкненому стані знаходиться на межі стійкості (запас по фазі дорівнює нулю). Накінець, розімкнена стійка система, яка має АФХ в формі кривої 3, в замкненому стані буде нестійкою з недоліком фази, що відповідає кривій 2. Аналізуючи форми ЛАФЧХ для стійких і нестійких систем, можеа сформулювати наступний логарифмічний критерій стійкості: динамічна лінійна система, стійка в розімкненому стані, стійка і в замкненому стані, якщо на всьому діапазоні частот, на якому L(ω)>0, значення фази φ(ω)>-180°. Під частотою зрізу ω _зр розуміється частота, при якій L(ω) перетинає вісь частот.

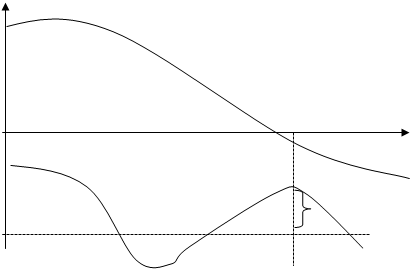
Для стійких розімкнених лінійних систем, які мають АФХ другого роду (рис 3.3 б)), логарифмічний критерій стійкості може бути сформульований так: лінійна динамічна система, стійка в розімкненому стані, буде стійкою і в замкненому стані, якщо на всьому діапазоні частот, на якому L(ω) > 0, кількість додатніх переходів фазової характеристики (ФХ) через лінію OX рівна кількості від’ємних переходів (рис 3.5).

L(ω)

0 ω

φ(ω) (+) α

(-)

Рис 3.5 Загальний випадок логарифмічного критерія стійкості

Виділення областей стійкості. Критерій Вишнеградського.

При налагоджуванні та експлуатації лінійних динамічних систем виникає необхідність змінювати окремі параметри системи, отже, неодноразово перевіряти систему на стійкість. Тому важливе значення мають методи, які дозволяють визначити область зміни тих чи інших параметрів, припустиму з точки зору умов стійкості. Так як коефіцієнти характеристичного рівняння системи визначаються через її параметри,то поставлена задача визначення припустимого по умовам стійкості діапазона зміни коефіцієнтів характеристичного рівняння.

Така задача для діапазона зміни двух параметрів була вперше поставлена і вирішена російським інженером та вченим І.А. Вишнеградським. Результат розв’язку відомий під назвою діаграми Вишнеградського, які широко і успішно застосовуються на практиці аналізу та синтезу лінійних систем автоматичного управління.

Критерій Вишнеградського обгрунтований для систем, які описуються лінійними рівняннями третього порядку, але ідеї, закладені в цьому критерії, дуже вплинули на розвиток теорії стійкості лінійних динамічних систем.

Нехай є система, характеристичне рівняння якої має вигляд

а₀ р³ + а₁ р² + а₂ р + а₃ = 0, (3.12)

або р³ + с₁ р² + с₂ р + с₃ = 0. (3.13)

де: с₁ = а₁ / а₀ ; с₂ = а₂ / а_0; с₂ = а₃ / а₀.

Зробимо підстановки р = Z³v c₃; c₁ = X ³v c₃; c₂ = Y ³v c₃² або Z = p/ ³v c₃; X = c₁/ ³v c₃; Y = c₂/ ³v c₃².

З урахуванням цих позначень рівняння (3.13) прийме вигляд:

Z³ + X Z³ + YZ + 1 = 0.

Якщо система знаходиться на межі стійкості, то рівняння (3.13) буде мати один дійсний від’ємний корінь та два уявних кореня:

р₁ = - α; р₂ = - jβ; р₃ = jβ.

Ліву частину рівняння (3.13) можна розкласти на множники:

р³ + с₁ р² + с₂ р + с₃ = р³ + р²α рβ² + αβ²

Прирівнюючи в цьому рівнянні коефіцієнти при однакових ступенях р, знаходимо с₁ = α, с₂ = β², с₃ = αβ².

З урахуванням цих співвідношень справедливо:

с₁ с₂ – с₃ = 0 (3.14)

Виразивши в (3.14) коефіцієнти через X і Y, отримаємо

XY – 1 = 0, тобто XY = 1. (3.15)

Це рівняння є рівнянням гіперболи, коефіцієнти якого виражені через коефіцієнти характеристичного рівняння системи, тобто через її параметри. При цьому, як слідує з приведених міркувань, всі точки в площині Y,Z, які лежать на гіперболі (3.15), відповідають таким значенням параметрів системи, при яких ця система знаходиться на межі стійкості. Геометричне місце точок на площині параметрів лінійної динамічної системи, яка описується диференціальним рівнянням третього порядку, відповідне стану системи на межі стійкості, називається гіперболою Вишнеградського – рівняння (3.15). Гіпербола Вишнеградського розбиває площину Y, X на дві області: XY < 1 (область І) і XY > 1 (область ІІ). Для з’ясування питання про стійкість системи з параметрами, які лежать в областях І і ІІ, приймемо в рівнянні (2.73) с₃ = 0. Тоді отримаємо: р=0; р² + с₁ р + с₂ = 0. Друге рівняння буде мати корені з від’ємними дійсними частинами при умові: с₁>0; с₂>0. Враховуючи, що с₃=0, приходимо до висновку, що два кореня мають від’ємні дійсні частини при умові:

с₁ с₂ – с₃ > 0. (3.16)

Ця умова залишається справедливою й у випадку, коли с₃ відрізняється від нуля, так як при малій зміні с₃ корені рівняння (3.15) змінюються мало, згідно теореми про неперервність залежності коренів характеристичного рівняння від його коефіцієнтів. Отже, умова (3.16) є умовою стійкості системи, яка, з урахуванням значень с₁, с₂, с₃, може бути замінена умовою: XY > 1.

Таким чином, область параметрів системи, розташована вище гіперболи Вишнеградського, відповідає області стійкості, а область, розташована нижче гіперболи - нестійка область.

На основі сказаного критерій стікості Вишнеградського формулюється так: лінійна динамічна система, яка описується диференційним рівнянням третього порядку, стійка, якщо про додатніх коєфіцієнтах характеристичного рівняння виконується умова XY > 1.

Стійку область на діаграмі Вишнеградського можна розбити на ряд підобластей з однаковим характером стійкого перехідного процесу. Наприклад, аналіз рівняння (3.16) з умов наявності трьох дійсних від’ємних коренів дозволяє виділити криву ECD, яка описується рівнянням 4(x³ + y³) – x² y² – 18xy + 27 = 0, яка на діаграмі виділяє область ІІІ. В межах цієї області параметри системи забезпечують від’ємні дійсні корені, тобто забезпечують аперіодичний перехідний процес в системі.

Розмірковуючи анатогічно, можна отримати рівняння кривої FCE (2x³ – 9xy + 27 = 0), яка виділяє в площині X, Y область IV з параметрами системи, які забезпечують один дійсний від’ємний корінь та два комплексних кореня з від’ємною дійсною частиною. При цьому дійсні частини комплексних коренів по абсолютному значенню більше дійсного кореня, що відповідає монотонним перехідним процесам. Накінець, в області ІІ має місце один дійсний від’ємний корінь та два комплексних кореня з від’ємною дійсною частиною. При цьому дійсний корінь по абсолютному значенню більший дійсних частин комплексних коренів, що відповідає коливальним перехідним процесам.

Таким чином, діаграма Вишнеградського представляє собою площину двух параметрів лінійної динамічної системи третього порядку з виділеними стійкими та нестійкими областями парметрів системи та областями, які відповідають аперіодичним та коливальним перехідним процесам. По діаграмі легко визначається діапазон зміни двух параметрів лінійної динамічної системи, який забезпечує той чи інший перехідний процес в системі.

Виділення областей стійкості на площині лінійної динамічної системи, яка описується диференційним рівнянням n-го порядку, здійснюється на базі загального методу D – розподілу, який розглядається в спеціальних курсах по теорії автоматичного управління. Цей метод базується на аналізі характеристичного рівняння лінійної системи. Він дозволяє порівнянно легко визначити припустимі з точки зору стійкості діапазони зміни одного чи двух коефіцієнтів характеристичного рівняння, які виражаються через параметри системи.

Контрольні запитання до лекцйї 3

1. Яким чином реалізується лінеарізація рівнянь?

2. Вкажіть на особливості математичного опису лінійних систем автоматичного управління?

3. Як відбувається ідентифікація об'єктів управління?

4. Що таке управляємість і споглядання?

5. Використання перетворень Лапласа і Фурье для укладання і рішення динаміки елементів і систем автоматичного управління.

6. В чому суть практичного використання алгебраїчного критерія Рауса?

7. Аналіз стійкості лінійної системи за критерієм Гурвіца.

8. Яким чином і коли необхідно використовувати частотний критерій стійкості – критерій Михайлова?

9. Що представляє собою діаграма Вишнеградського?

Лекція 4. Якість управління в ланайних динамічних системах

Під якістю управління розуміється характер перехідних процесів в системі, викликаних управляючими та збурюючими впливами. Закони зміни величин, які характеризують систему, задаються. Дослідження якості процесу управління зводиться, таким чином, до визначення дійсного характеруперехідних процесів в системі та порівнянню його з заданими законами. Якщо система не задовольняє потрібним показникам якості управління, то в неї вводяться додаткові елементи – корегуючі пристрої, які, не порушуючи основного призначення системи, забезпечують потрібну якість управління.

Для оцінки якості управління необхідно мат кількісні та якісні показники, які характеризують форми перехідних процесів в системі.

Оцінки якості управління можуть бути непрямими або прямими.

Непрямі оцінки отримують на основі аналізу тих чи інших характеристик системи, наприклад частотних. Непрямі методи оцінки дозволяють отримати деякі параметри перехідного процесу, наприклад встановити його принциповий характер – збіжний він чи розбіжний.

Серед непрямих методів оцінки якості процесу управління отримали розповсюдження кореневі, інтегральні та частотні методи.

Кореневі методи витікають з наявності зв’язку між формою перехідного процесу в системі і характером розподілу на комплексній площині коренів характеристичного рівняння. Наприклад, раніше було показано, що якщо є хоча б один правий корінь, то перехідний процес в системі буде розбіжним. Кореневі методи найбільш ефективні, якщо вдається виконати аналіз не тільки полюсів, а й нулів передаточної функції, тобто характеристичного полінома Н(р) = 0, а під нулями – корені чисельника передаточної функції, тобто полінома К(р) = 0.

Разом з тим кореневі методи найбільш повно розроблені для систем з передаточними функціями виду W(p) = k / H(p), тобто з передаточними функціями, які не містять нулів.

В інтегральних методах оцінками якості служать визначені інтеграли по часу від деякої функції фізичних величин, що характеризують систему, які обчислюються без розв’язку диференційного рівняння системи. Інтегральні методи найбільш зручні для порівняльної оцінки узагальнених показників якості в системах управління, близьких за деякими властивостями.

Частотні методи базуються на зв’язку між формою перехідного процесу в системі та дійсною частиною частотної характеристики. Ці методи дозволяють приблизно побудувати всю криву перехідного процесу, не розв’язуючи диференційних рівнянь, які описують систему, яка досліджується.

До прамих оцінок відносяться кількісні показники форми перехідного процесу фізичних змінних в системі при заданих впливах на неї. Пряма оцінка якості може бути отримана лише після того, як побудована залежність x(t), яка нас цікавить.

Побудова перехідних процесів операторним методом

Операторний метод аналізу якості управління базується на використанні передаточної функції системи, з якої можна отримати зображення шуканої величини:

x(p)=K(p)/H(p)F(p), (4.1)

де: F(p) – перетворена за Лапласом фукція впливу на систему (управляючого чи збурюючого).

Маючи зображення шуканої змінної x(p) та застосовуючи зворотнє перетворення Лапласа, можна визначити перехідний процес в системі, тобто функцію x(t).

Вираз (4.1) дозволяє знайти зображення функції перехідного процесу лише при нульових початкових умовах, що витікає з визначення передаточної функції системи. Як відомо, початкові умови будуть нульовими тоді, коли в початковтй момент впливу на систему сама функція x(t) та всі її похідні до (n-1)-ї включно рівні нулю. Початкові умови залежать від стану системи в момент прикладення збурюючого впливу та від його форми, яка визначається видом полінома К(р) – полінома чисельника передаточної функції системи. Можна виділити наступні обставини, які забезпечують нульові початкові умови:

1) початкові умови будуть нульовими при будь-якому впливі на систему, якщо в момент його прикладення система знаходилася в рівноважному стані, і поліном К(р) = k, тобто не містить р;

2) система в момент прикладення впливу знаходилась в рівноважному стані, в числі членів полінома К(р) маються такі, які містять р, але всі похідні функції впливу на систему, аж до m-ї включно, при t = 0 рівні нулю (тут m – порядок полінома К(р));

3) система знаходилась в нерівноважному стані, поліном К(р) містить члени, які містять р, але форма збурюючого впливу така, що при t = 0 кожний член правої частини диференційного рівняння руху системи, що містить похідну впливу на систему до m-ї включно, врівноважується відповідним членом лівої частини рівняння, який містить похідну збурення того ж порядку.

При ненульових початкових умовах зображення вихідної величини системи має вигляд:

x(p)=K(p)/H(p)F(p)+M(p)/H(p), (4.2)

де: M(p) – поліном, який враховує вплив ненульових початкових умов.

Для множини випадків зображення функції впливу на систему має вид дробно-раціонального виразу F(p) = F₁(p) / F₂(p). Тоді (4.2) прийме вигляд:

x(p) = (K(p)F₁(p) + F₂(p)M(p)) / (H(p)F₂(p))

Лінійні динамічні системи часто досліджуються в режимі впливу в формі одиничного стрибка f:

0 при t < 0

f = f (t) F при t > 0.

В цьому випадку:

F(p) = f / p; F₁(p) = f; F₂(p) = p.

Тоді (4.2) прийме вигляд:

x(p)=(K(p)f+pM(p))/(pH(p)). (4.3)

Якщо в (4.3) корені поліному Н(р) = 0 будуть простими (не кратними) і при t = 0 система знаходиться в рівноважному стані, то, використовуючи формулу розкладення Хевісайда, отримаємо:

x(t)=K(0)/H(0)+Σ[K(p)/ (p H΄(p))] _p=pk ^epkt, (4.4)

де: H΄(p) = [ d /dt H(p)] _p=pk, n – порядок полінома Н(р) = 0; р₁, р₂,…р_n – корені полінома Н(р)= 0; К(0) = К(р) і Н(0) = Н(р) при р = 0.

На основі властивостей полінома Н(р)=0, його можна представити у виді:

Н(р) = а₀ (р - р₁) … (р – р_k) … (p – р_n) = a₀ Π (p – р_k);

H΄(p) = (р_k - р₁) … (р_k – р_n) = Π (р_k – р_q).

Тоді (4.4) можна переписати так:

x(t)=K(0)/H(0)+Σ[K(р_k)/(р_kΠ(р_k–р_q)) e^pkt ]. (4.5)

Вираз (2.81) дозволяє побудувати перехідний процес x(t) в лінійній динамічній системі при одиничному впливу.

Операторний метод побудови перехідних процесів стає незручним для систем високого порядку, так як вимагається великий об’єм обчислень.

Побудова перехідних процесів частотним методом

Метод базується на використанні частотної характеристики Р(ω) дійсної частини виразу передаточної функції W(p) системи при р= jω:

W(jω) = P(ω) + jQ(ω). (4.5)

Не зупиняючись на доведенні, вкажемо, що між функціями x(t) і Р(ω) має місце наступні залежності:

x(t)=2/πω_0іP(ω)/ωsin(ωt)dω, (4.6)

або:

x(t)=P(0)+2/πω_0іQ(ω)/ωcos(ωt)dω (4.7)

Функції P(ω) та Q(ω) важко описати аналітично. Тому перехідні процеси безпосередньо по виразам (4.6) і (4.7) на практиці не розраховуються. Проте розрахунок суттєво спрощується, якщо криву P(ω) замінити сукупністю трапецій:

P(ω) = Σ P_і(ω), (4.8)

де: і – номер трапеції.

Кожній складовій P_і(ω) відповідає перехідний процес вигляду:

x_і(t) = 2/π ω_0і P_i(ω) / ω sin(ωt) dω.

Таким чином, x(t)=Σx_і(t). (4.9)

Вираз (4.9) лежить в основі методу розрахунку перехідних процесів в лінійних динамічних системах з використанням дійсної частотної характеристики P(ω). Для практичної реалізації метода кожну і-ту трапецію визначимо наступними параметрами: P_0і - висота; ω_0і - інтервал пропускання частот; ω_dі – інтервал рівномірного пропускання частот; ν=ω_dі/ω_0і - коефіцієнт нахилу. Крім того, вводиться поняття типової одиничної трапеції, для якої прийнято Р₀ = 1, ω₀ = 1 при будь-якому значенні ν.

Залежність (4.6) для випадку, коли Р(ω) заінюється типовою одиничною трапецією, дає наступні вирази перехідного процеса:

h(t)=2/(π(1-ν))[Si(T)-νSi(νT)+(cos(T)-cos(νT)/T], (4.10)

де: Si(τ) – інтегральний сінус виразу sin τ / τ)dt.

Функція h_i(t) легко перетворюється у відповідну функцію х_i(t) шляхом перахунку масштабу по осям. Грунтуючись на зв’язку характера функції Р(ω) і функції переходного процесу цей перерахунок здійснюється так:

х_i(t)=h_i(τ)ω_0і; t=τ/ω_0i (4.11)

Значення функції h(τ) для різних значень ν і τ розраховані та зведені в таблиці, які дозволяють легко отримати точки кривої х_i(τ).

На основі викладеного порядок побудови графіка перехідного процесу в лінійній динамічній системі при одиничному впливі на вході з використанням дійсної частотної характеристики зводиться до такої послідовності операцій:

1) на основі передаточної функції системи W(p) шляхом заміни р на jω та відокремлення дійсної частини від уявної знаходиться характеристика Р(ω);

2) функція Р(ω) розподіляється на трапецієвидні складові, для кожної з яких визначаються параметри Р_0і, ω_0і, ω_dі, ν;

3) за допомогою таблиць знаходяться h -функції для відносного часу тьсвикористовуючи співвідношення маштабів;

4) визначається крива перехідного процесу в системі як алгебраїчна сума кривих х_i(t): x(t) = Σ x_і(t), де: n – число трапецій, якими замінена характеристика Р (ω)_. Розглянутий метод можна розповсюдити на побудову перехідних процесів при впливу, що відрізняється від одиничного, про що піде мова нижче.

Як, відмічалося, перехідні процеси в лінійних динамічних системах будуються звичайно для замкнених систем. Тому найбільш трудомісткою частиною розрахунку є визначення характеристики Р(ω) замкненої системи. Ця частина розрахунку суттєво спрощується при використанні для визначення дійсної частотної характеристики Р(ω) замкненої системи характеристик L(ω) і ν(ω) розімкненої системи. В теорії автоматичного управління широко використовуються номограми для визначення функції Р(ω) замкненої системи за логарифмічними амплітудно-фазовим частотним характеристикам розімкненої системи.

Від перехідного процесу, викликаного одиничним вхідним впливом, можна перейти до перехідного процесу від довільного впливу u(t), використовуючи інтеграл Дюамеля, або згортання:

x(t)=u(t-τ)ω(τ)dτ, (4.12)

або:

x(t) = ω (t - τ) u(τ) dτ

де: u(t); ω(t) – імпульсна перехідна функція.

Імпульсна перехідна функція ω(t) представляє собою перехідний процес в системі, до якої прикладений імпульсний вплив у виді δ -функції яка відповідає умові

δ(t)dt =1; δ(p)=1, (4.13)

де δ -функція існує тільки при t = 0.

Неважко впевнитися, що між імпульсною перехідною функцією ω (t) і функцією h(t) існує залежність:

ω(t)=h^΄(t), (4.14)

тобто, ω(t) представляє собою першу похідну за часом h-функції – функції перехідного процесу при одиничному збуренні.

Контрольні запитання до лекції 4.

1. Як хароктеризуються і чим відрізняються логарифмічні (ЛАХ), амплітудно-фазові (АФХ), частотні характеристики (ЛАФЧХ)?

2. Який алгоритм побудова частотних характеристик лінійних САУ?

3. Визначення стійкості. Постановка задачі аналізу САУ на стійкість.

4. Що таке загальність лінійних умов систем управління; принцип лівих коренів?

5. Опишіті всі відомі вам критерії стійкості: алгебраїчні і частотні.

6. Що розуміється під областю стійкості САУ?

7. Визначення поняття "якість управління". Яким чином це поняття застосовується на практиці?

8. Прямі і побічні засоби оцінки якості управління. Засоби розрахунку перехідних процесів в лінійних САУ.

Лекція 5. Корекція лінійних динамічних систем.

Лінійну динамічну систему, елементи якої розраховані з умов забезпечення статичних режимів роботи, будем називати початковою системою. Початкова система може виявитись незадовільною з точки зору вимог динаміки, тобто нестійкою або стійкою, але не такою що забезпечує необхідних форм перехідних процесів. В таких випадках початкова система доповнюється спеціальними елементами –коригуючими пристроями (КП), які вводяться в систему з метою придання їй необхідних динамічних властивостей, не змінюючи основного призначення системи, що визначається умовами роботи об’єкту управління.

За характером включення коригуючих пристроїв в початкову систему їх можна поділити на дві групи – послідовні коригуючі пристрої (КП) та паралельні. Перші вмикаються послідовно з елементами початкової системи, другі – паралельно будь–яким елементам. Паралельні КП є місцевими зворотніми зв’язками, які можуть бути як від’ємними, так і додатніми.

Зупинимось на одму, простому та ефективному способі визначення математичних моделей КП і відповідних цим моделям фізничних елементів, формуючих коригуючі пристрої. Спосіб базується на так званих бажаних логарифмічних амплітудно – частотних характеристиках (L_ж). Бажаною ЛАЧХ називається така характеристика (L_w), яка відповідає лінійній динамічній системі, повністю відповідає вимогам, що пред’являються в динамічних режимах. Можна сформулювати вимоги до форми L_ж для широкого кола статичних та астатичних систем.

Найбільший вплив на динаміку чинить форма L_ж(w) в районі частоти зрізу w_ср. У зв’язку з цим весь діапазон частот характеристики L_ж(w) (рис. 2.12) розіб’єм на три частини: ділянка низьких частот (0<w<w₁); ділянка середніх частот (w₂<w<w₃); високочастотна ділянка (w>w₃).

L_ж(w)

20lgk

w₁ w₂ w_ср w₃ w

Рис.5.1 Характеристика L_ж(w).

Побудова характеристики L_ж(w) починається з вибору значення частоти w_ср, яка прямо пов’язана з швидкодією системи. Меньші значення w_ср відповідають меньшій швидкодії системи, тобто непереборні труднощі в практичній реалізації цієї характеристики, так як будуть потрібні дуже складні, включно до нереалізуємих відображають більшу тривалість перехідних процесів. При виборі значних частот w_ср для характеристики L_ж(w) можуть виникнути фізичними елементами, коригуючі пристрої.

В практиці проектування лінійних динамічних систем широко використовують залежності, що пов’язують значення w_ср з величинами t_max і d_max, де: t_max – максимальний час перехідного процесу; d_max –максимальне перерегулювання. Використовуючи ці залежності, можна вибрати значення w_ср, що забезпечує потрібні показники якості управління в проектуємій системі.

Аналіз систем, що мають високі динамічні якості, показує що ЛАЧХ таких систем повинна мати в районі частоти зрізу нахил –20 дБ/дек. Отже, середньочастотна ділянка характеристики L_ж(w) являє собою лінію CD (рис. 5.1), що проходить через точку w_ср з нахилом -20дБ/дек. Межі ділянки CD визначаються ординатами L₂ і L₃, що відовідають частотам w₂ і w₃, які також можуть бути визначені по заданим значенням d_max.

Ділянка характеристики L_ж(w) правіше точки D проводиться з таким нахилом, який має ЛАЧХ початкової системи в цьому діапазоні частот, так як високочастотна ділянка L_ж(w) практично не впливає на показники якості управління.

Низькочастотна ділянка L_ж(w) для статичних систем являє собою пряму АВ, яка є паралельною осі частот і проходить на висоті 20 lgk, де k – коефіцієнт підсилення початкової розімкненої системи. Для астатичних систем ця ділянка характеристики являє собою пряму лінію з нахилом – 20n дБ/дек., де n - порядок астатизму, що проходить через точку з координатами [w = 1; L(w) = 20 lgk]. Нарешті, низькочастотна і середньочастотна ділянки ЛАЧХ об’єднують відрізком ВС (або більш ніж одним відрізком). Нахил відрізка ВС обирається з умови, щоб перепад нахилів двух сусідніх відрізків характеристики L_ж(w) не перевищував 40 дБ/дек. Ця вимога витікає з можливостей реальних фізичних елементів, з допомогою яких реалізується характеристика L_ж(w).

Для визначення типу і параметрів КП на базі використання характеристики L_ж(w) необхідно порівняти цю характеристику з ЛАЧХ L_поч(w) вихідної системи і встановити вид ЛАЧХ що вимагає коригуючого пристрою, тобто форму характеристики L_к.у(w).

Якщо синтезується послідовне КП, то:

W_ск(р) =W_поч(р) W_к.у(р),

де: W_ск(р), W_поч(р) – передаточні функції відповідно скоригованої і вихідної систем; W_к.у(р) – передаточна функція послідовного корегуючого пристрою.

Переходячи від передаточних функцій до АФХ, а потім до ЛАЧХ, отримаєм L_ск(w) = L_поч(w) + L_к.у(w).

Так як мета корегування зводиться до того, щоб перетворити початкову систему в бажану з точки зору динамічних властивостей, то очевидно, що L_ск(w) = L_ж(w), звідси випливає, L_к.у(w) = L_ж(w) - L_поч(w). Таким чином, якщо з ординат характристики L_ж(w) відняти ординати характеристики L_поч(w), то отримаєм ординати ЛАЧХ послідовного КП. Далі по виду L_к.у(w) можна вибрати фізичні елементи, що реалізує цю ЛАЧХ, тобто вибрати фізичну схему і параметри КУ.

При виборі паралельного КУ:

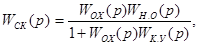
де: W_охв(р), W_н.о(р) - передаточні функції частини початкової системи відповідно охопленої місцевим зворотнім зв’язком (паралельним КП) і не охопленої нею.

Переходячи до АФХ, отримаєм:

Для діапазона частот, в якому , маємо: W_cк(jw)» W_н.о(jw)/ W_к.у(jw).

Переходячи до ЛАЧХ, отримаєм:

L_к.у(w) = L_н.о(w) - L_ск(w),

тобто, ЛАЧХ паралельного корегуючого пристрою має вигляд:

L_к.у(w) = L_н.о(w) - L_ск(w).

На основі останнього виразу можна визначити логарифмічну частотну характеристсику паралельного КП, вибрати фізичні елементи та їх параметри, що реалізують L_к.у(w). У практиці проектування лінійних динамічних систем широко використовуються таблиці, що містять фізичні схеми КП, іх передаточні функції та характеристики L_к.у(w). У таких випадках задача вибору КП зводиться до визначення вищевказаним способом форми L_к.у(w) і вибору в таблицях необхідного типу корегуючого пристрою.

Доцільно підкреслити, що вирішення задачі вибору КП неоднозначне, так як одні і тіж динамічні характеристики можна забезпечити різноманітними фізичними елементами, що утворюють корегуючі пристрої. Наприклад, в практиці автоматичного управління широко використовуються паралельні КП, що реалізують гнучкий зворотній зв’ язок по різноманітним фізичним змінним, що подаються на вхід КП, з виходу охопленої частини лінійної системи. Такі КП мають передаточну функцію виду:

W(p)=T₂(p)/(T₁(p)+1).

Цю передаточну функцію і відповідну Їй L_к.у(w) можна реалізувати з допомогою декількох пристроїв, частина яких приведена на рис. 2.13. Постійні часу і коефіцієнти підсилення їх встанолюються наступним чином:

- для стабілізаційного трансформатора:

; ; ;

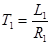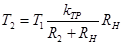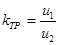- для динамічного моста:

; ; .

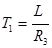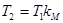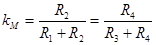Контрольні запитання до лекції 5

1. Який алгоритм розрахунку перехідних процесів в САУ засобами чисельного інтегрування Эйлера і Рунге - Кутта з використанням ЕОМ?

2. Частотні засоби оцінки якості: зв'язок тимчасових і частотних характеристик, близька оцінка параметрів якості по амплітудно-фазовым і логарифмическим характеристикам лінійних систем.

3. Яким чином проводяться дослідження якості автоматичних систем на ЕОМ з використанням пакетів прикладних програм і алгоритмічних мов моделювання?

4. Що таке Z-перетворення, перетворення Лапласа?

5. Опишіть передаточні функції елементів імпульсних систем.

6. Якими є передаточні функції розімкнутих і замкнутих імпульсных САУ?

7. Визначення і область використання оптимальних і адаптивних автоматичних систем.

8. Якими є критерії оптимальності, що реалізуються в системах автоматичного управління? Математичний опис оптимальних САУ.

СПИСОК ЛІТЕРАТУРИ

1. Михайлов В.С. Теория управления. –К.: Вища шк. Головное изд-во, 1988.-312 с.

2. Теорія автоматичного управління: Учеб. пособ. Под. ред. А. А. Воронова. - М.: Высш. шк., 1986. – ч.1-337 с., ч. 2-504 с.

3. Солодовников В. В., Плотников В. І., Яковлев А. В. Основи теории и елементы систем автоматического регулирования: Учеб. Пособ.- М.: Машиностроение, 1985. – 536 с.

Навчально-методичне видання

ЦЮЦЮРА Світлана Володимирівна

ТЕОРІЯ УПРАВЛІННЯ

Конспект лекцій

Бухгалтерский учет в Российской Федерации должен осуществляться в соответствии с нормативными документами, принятыми и утвержденными органами власти различного уровня. Основными из них являются:

· Конституция РФ;

· Гражданский кодекс РФ (ч. 1—3);

· Налоговый кодекс РФ (ч. 1—2);

· Трудовой кодекс РФ;

· Федеральный закон от 21 ноября 1996 г. № 129-ФЗ «О бухгалтерском учете»;

· Положение по ведению бухгалтерского учета и бухгалтерской отчетности в Российской Федерации (утв. приказом Минфина России от 29 июля 1998 г. № 34н с посл. изм. и доп.);

· Положения по бухгалтерскому учету (ПБУ);

· План счетов бухгалтерского учета и Инструкция по его применению (утв. приказом Минфина России от 31 октября 2000 г. № 94н);

В совокупности, перечисленные и другие документы образуют четырехуровневую систему нормативно-правовых актов, регулирующие ведение бухгалтерского учета.

1- законодательный (Федеральный закон «О бухгалтерском учете» и другие федеральные законы,

2 - стандарты (положения) по бухгалтерскому учету и отчетности;

3 - методические рекомендации (инструкции, письма Минфина России и др.);

4 - рабочие документы по бухгалтерскому учету экономического субъекта и прежде всего приказ по учетной политике.

Федеральный закон «О бухгалтерском учете» - правовые основы бухгалтерского учета, его содержание, принципы, организацию, основные направления бухгалтерской деятельности и составления отчетности, хозяйственные субъекты, которые обязаны вести бухгалтерский учет и представлять финансовую отчетность.

На основе Федерального закона «О бухгалтерском учете» Правительством РФ утверждено Положение по ведению бухгалтерского учета и бухгалтерской отчетности в Российской Федерации. Положение закрепило базовые понятия, порядок организации и ведения бухгалтерского учета и другие положения Закона «О бухгалтерском учете». В настоящее время также разработаны и утверждены положения по бухгалтерскому учету (ПБУ), представляющие собой свод основных правил, устанавливающих порядок учета и оценки определенного объекта, вот некоторые из них:

ПБУ 1/98 «Учетная политика предприятия»;

ПБУ2/94 «Учет договоров (контрактов) на капитальное строительство»;

ПБУ3/2006 «Учет активов и обязательств, стоимость которых выражена в иностранной валюте»;

Методические рекомендации, разрабатываемые Министерством финансов РФ и различными ведомствами, предназначены для конкретизации учетных стандартов в соответствии с отраслевыми особенностями.

Рабочие документы самой организации определяют особенности организации и ведения учета в ней. Основными из них являются утвержденные руководителем предприятия учетная политика предприятия и формы первичных учетных документов; графики документооборота, рабочий план счетов бухгалтерского учета.

4. Положение по ведению бухгалтерского учёта и бухгалтерской отчётности в РФ

На основе Федерального закона «О бухгалтерском учете» Правительством РФ утверждено Положение по ведению бухгалтерского учета и бухгалтерской отчетности в Российской Федерации. Положение закрепило базовые понятия, порядок организации и ведения бухгалтерского учета и другие положения Закона «О бухгалтерском учете». В настоящее время также разработаны и утверждены положения по бухгалтерскому учету (ПБУ), представляющие собой свод основных правил, устанавливающих порядок учета и оценки определенного объекта:

ПБУ 1/98 «Учетная политика предприятия»;

ПБУ2/94 «Учет договоров (контрактов) на капитальное строительство»;

ПБУ3/2006 «Учет активов и обязательств, стоимость которых выражена в иностранной валюте»;

ПБУ 4/99 «Бухгалтерская отчетность организации»;

ПБУ 5/01 «Учет материально-производственных запасов»;

ПБУ 6/01 «Учет основных средств»;

ПБУ 9/99 «Доходы организации»;

ПБУ 10/99 «Расходы организации»;

ПБУ 12/2000 «Информация по сегментам»;

ПБУ 13/2000 «Учет государственной помощи»;

ПБУ 14/2007 «Учет нематериальных активов»;

ПБУ 15/01 «Учет займов и кредитов и затрат по их обслуживанию»;

ПБУ 16/02 «Информация по прекращаемой деятельности»;

ПБУ 17/02 «Учет расходов на научно-исследовательские, опытно-конструкторские и технологические работы»;

ПБУ 18/02 «Учет расчетов по налогу на прибыль»;

ПБУ 19/02 «Учет финансовых вложений»;

ПБУ 20/03 «Информация об участии в совместной деятельности».

Методические рекомендации, разрабатываемые Министерством финансов РФ и различными ведомствами, предназначены для конкретизации учетных стандартов в соответствии с отраслевыми особенностями.

Рабочие документы самой организации определяют особенности организации и ведения учета в ней. Основными из них являются утвержденные руководителем предприятия учетная политика предприятия и формы первичных учетных документов; графики документооборота, рабочий план счетов бухгалтерского учета.

7. История возникновения и основные этапы развития бухгалтерского учёта

Зародился бухгалтерский учет в XIII в., а в XV в. вышла книга Л. Пачоли о бухгалтерском учете (трактат). В XX в. началось литературное осмысление бухгалтерского учета, т. е. возникли первые теоретические конструкции бухгалтерского учета (счетоведение).

Бухгалтерский учет развивался под воздействием внешних причин (необходимости вести хозяйство), затем внутренних (шло саморазвитие).

Для возникновения бухучета были необходимы два главных фактора:

1) хозяйство должно достигнуть значительных размеров (требуется его учет);

2) возникает алфавит и элементарная арифметика.

В Древнем Египте каждые 2 года осуществлялась инвентаризация всего недвижимого и движимого имущества.

При появлении денег в виде монет, которые выступают как самостоятельный объект учета (средство в расчетах), стала вестись хронологическая запись всех фактов хозяйственной жизни. Также ввелись зачетные платежи, стали производиться переводы платежей в другие кассы. Существует периодическая публичная отчетность. Происходит разделение бухгалтера и ревизора (они равноправны).

Экономический рост стран Европы и зарождение капиталистических отношений, развитие кредита, возникновение фирм – все это привело к возникновению двойной записи в Северной Италии около 1250–1350 гг., автором которой считают итальянца Л. Пачоли (1445–1515).

В конце XIX в. из практики выделилась теория, появились первые вычислительные аппараты, усилились экономические аспекты учета, бухгалтерский учет сблизился со статистикой.

В 1930–х гг. в понятия бухучета «капитал» и «пассив» были сплочены под общим названием «пассив», и это осталось до сих пор. В учете обязательства рассматриваются как чужой капитал (заемный), т. е. так же, как один из источников имущества, который вместе с собственным капиталом и составляет пассив.

С развитием капитализма возникает необходимость в расширении учетного аппарата и разделения учетного труда.

Соответственно с дальнейшим развитием экономики для каждого главного счета стали вести отдельный журнал. По их итогам можно составить баланс. Одновременно заменяются бухгалтерские книги карточками и ведомостями. Широкое развитие в 1920–х гг. получают карточки, а также копирование записей (запись в карточке копируют в журнал).

Вторая половина XIX и начало XX века стали по существу этапом становления бухучета как науки. Этому во многом способствовали появление крупной промышленности, развитие путей сообщения, увеличение оборотов мировой торговли, возн

Дата добавления: 2014-01-11