Пример применения

Остаточные члены формул трапеций и парабол.

Без доказательства приведем оценки сверху остаточных членов формул трапеций и парабол: ; .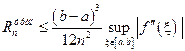

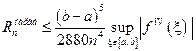Вычислить , с точностью до 10^–6.

С целью применения формулы Симпсона находим производные до четвертой включительно:

.

Чтобы исследовать поведение y ⁽⁴⁾, найдем y ⁽⁵⁾:

; ;

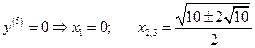(при этом x ₂» 0,96; x ₃» 2,02).

И можно построить эскиз графика функции y ⁽⁴⁾(x):

В свете выше сказанного, целесообразно, вычисляемый интеграл представить как сумму трех интегралов: .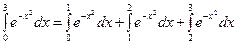

*) Для x Î[1; 2] .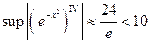

На интеграл 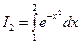выделим 0,7 разрешенной ошибки, ибо здесь труднее всего достигнуть необходимой точности. Оценивая остаточный член формулы Симпсона, получаем:

.

Отсюда n ³ 8.

При вычислении I ₂ по формуле Симпсона надо взять n = 8.

*) Для x Î[2; 3] .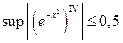

На интеграл 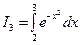выделим 0,2 разрешенной ошибки. Из условия

,

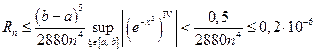получим n ³ 6.

При вычислении I ₃ по формуле Симпсона надо взять n = 6.

*) Для x Î[0; 1] .

Это довольно большая величина, что делает применение формулы Симпсона нецелесообразным. Вместо этого воспользуемся разложением в ряд Маклорена:

.

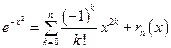В этом разложении, вследствие знакопеременности ряда имеем:

.

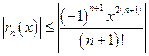Интегрирование разложения на [0; 1] дает: ,

а ошибка оценивается следующим образом:

.

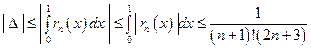Т.е. .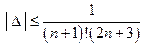

На интеграл осталось 0,1 допустимой ошибки

и отсюда n ³ 9.

При вычислении I ₁ с помощью разложения подынтегральной функции в ряд Маклорена достаточно взять n = 9.

Следует подумать и о том, с какой точностью вычисляются значения подынтегральной функции в точках разбиения для формулы Симпсона. Казалось бы, что, коль скоро, таких точек разбиения много, а каждые 10 слагаемых это один знак точности, то подынтегральную функцию надо вычислять со значительно большей точностью. Однако это не так, ибо в формуле Симпсона есть и деление на n, и, по сути, в точках разбиения достаточно вычислить с точностью в два раза большей, нежели вычисляемый интеграл.

РАЗДЕЛ 5. Ряды.

Дата добавления: 2014-01-11