Признаки сходимости знакопеременных рядов

а). Признак Лейбница для знакопеременных рядов.

Рассмотрим ряд: , 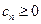. Если для указанного знакочередующегося ряда 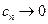и монотонно, то ряд сходится, вообще говоря, условно.

Δ Для ряда рассмотрим четные частные суммы ряда: . Если сгруппировать отдельные слагаемые по два начиная с первого, то получим 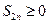, а при группировке отдельных слагаемых по два начиная со второго, получим 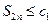. Таким образом последовательность четных частных сумм возрастающая и ограничена сверху. Тогда .

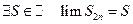Рассмотрим нечетные частные суммы того же ряда 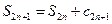и, переходя к пределу при , получим, что и, следовательно, т. е. ряд сходится. ▲

Пример: 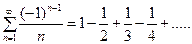сходится по Лейбницу, а – расходится, ибо это гармонический ряд. Следовательно, исходный ряд сходится условно.

б). Признаки Абеля и Дирихле.

Изучается сходимость рядов вида 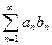. Обозначая =, проделаем следующее преобразование, которое принято называть преобразованием Лапласа.

= = =

= = .

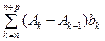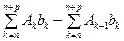Проделав такое преобразование, запишем:

(*)

Признаки Абеля и Дирихле сходимости рядов вида :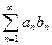

Пусть:

Абеля: Последовательность { b_n } монотонна и ограничена, а ряд 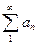сходится.

Дирихле: Последовательность { b_n } монотонно стремится к нулю, а частные суммы ряда 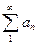ограничены в совокупность.

Тогда: ряд 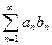сходится, вообще говоря, условно.

Δ. +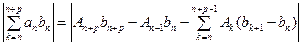

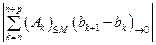
+ . Внизу, на месте индексов, в выражениях написаны оценки, следующие из условий признака Дирихле. Ряд сходится. Признак Дирихле доказан.

Запишем ряд 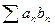в виде , где , т.к. 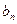– монотонна и ограничена, из условий признака Абеля. Тогда 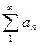сходится по условию, а 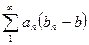сходится по Дирихле. Ряд сходится. Признак Абеля доказан. ▲

Интересная особенность: Признак Дирихле доказан с помощью преобразования Абеля, а признак Абеля доказан с помощью признака Дирихле.

Пример: а). Исследовать ряд на сходимость: .

Последовательность 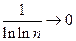и монотонна. = =

= = =

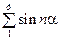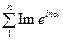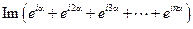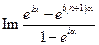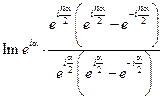
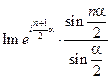= . Тогда 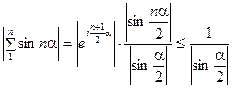, т.е. частные суммы ряда 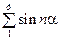ограничены. Ряд сходится по Дирихле, вообще говоря, условно.

Самое время поставить вопрос о абсолютной сходимости ряда.

Рассмотрим .

Первый из полученных рядов расходится по мажорантному признаку, т.к. 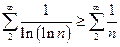. Второй из полученных рядов сходится по Дирихле (аналогично исходному ряду). Таким образом, ряд – расходится. Исходный ряд не сходится абсолютно, но сходится. Следовательно, ряд условно.

б). Исследовать на сходимость ряд .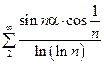

Прежде всего, обратим внимание на следующее ошибочное рассуждение: Т.к. при , то 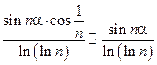. По асимптотическому признаку одновременной сходимости – расходимости рядов, ряды с эквивалентными членами сходятся или расходятся одновременно. В предыдущем примере показана сходимость ряда 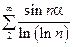. Следовательно, сходится и ряд 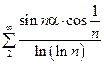. Ошибочность этого рассуждения заключается в том, что асимптотический признак одновременной сходимости –

расходимости рядов применим только к знакопостоянным рядам, а исходный ряд таковым не является.

И, тем не менее, исходный ряд сходится, что легко установить. Ряд 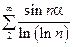сходится, как было установлено в предыдущем примере. А последовательность ограничена и монотонно стремится к единице. Ряд сходится по признаку Абеля.

Дата добавления: 2014-01-11