Определения. 3.4.1. Если существует число МÎR такое, что для хÎХ выполняется неравенство х<М

3.4.1. Если существует число МÎ R такое, что для " х Î Х выполняется неравенство х <М, то множество Х называется ограниченным сверх у (числом М). Число М называется верхней границей множества Х.

3.4.2. Если существует число mÎ R такое, что для " х Î Х выполняется неравенство х >m, то множество Х называется ограниченным сни зу (числом m). Число m называется нижней границей множества Х.

3.4.3. Если существует число МÎ R такое, что для " х Î Х выполняется неравенство | х |<М, то множество Х называется ограниченным.

Теорема 3.4.1. Множество ограничено тогда и только тогда, когда оно ограничено сверху и снизу.

Если множество Х ограничено сверху, то множество его верхних границ бесконечно (если число М - верхняя граница, то верхними границами будут числа М+1, М+2 и т.д.). Обозначим У множество верхних границ множества Х. Множество У ограничено снизу (любым элементом множества Х).

Возможны два случая: либо множество Х имеет максимальный элемент (например, если

Х – отрезок [0, 1], то максимальный элемент равен 1), в этом случае множество верхних границ не имеет минимального элемента; либо множество Х не имеет максимального элемента (например, если Х = (0, 1)), в этом случае множество верхних границ имеет минимальный элемент.

Определение 3.4.4. Точной верхней границей, или верхней гранью, множества Х, ограниченного сверху, называется максимальный элемент этого множества, если он существует, и минимальный элемент множества верхних границ, если множество Х не имеет максимального элемента.

Для обозначения применяются: символы sup X или sup{ x }.

Свойства верхней грани:

Пусть М^*= sup X - верхняя грань множества Х. Тогда

3.4.2. Для " х Î Х выполняется неравенство х £М^*.

3.4.3. Любое число, меньшее М^*, не будет верхней границей множества Х, т.е. для "e>0 $ x Î X такой, что х > М^*-e.

Аналогичным образом, если множество Х ограничено снизу, то множество его нижних границ бесконечно. Обозначим Z множество нижних границ множества Х. Множество Z ограничено сверху (любым элементом множества Х).

Определение 3.4.5. Точной нижней границей, или нижней гранью, множества Х, ограниченного снизу, называется минимальный элемент этого множества, если он существует, и максимальный элемент множества нижних границ, если множество Х не имеет минимального элемента.

Для обозначения применяются: символы inf X или inf{ x }.

Свойства нижней грани:

Пусть М_*= inf X - нижняя грань множества Х. Тогда

3.4.2. Для " х Î Х выполняется неравенство х ³ М_*.

3.4.3. Любое число, большее М_*, не будет нижней границей множества Х, т.е. для "e>0 $ x Î X такой, что х < М_*+e.

4. Предел функции одной переменной.

4.1. Определение функции. Терминология.

Пусть Х, Y - некоторые множества.

Опр.4.1.1. Функцией называется любое правило (закон), которое каждому элементу х Î Х ставит в соответствие определённый элемент у Î Y.

Обозначение функциональной зависимости: y = f (x) или f: X ® Y. Множество Х называется областью определения функции, множество Y_f = f (X) = { y | y = f (x), x Î X }Í Y - областью значений функции. (Смысл записи f: X ® Y состоит в том, что функция y = f (x) отображает множество Х в множество Y. Если образ множества X при отображении f: X ® Y полностью "накрывает" множество Y, т.е. Y_f = Y, то отображение f: X ® Y называется отображением Х на Y. Так, функция y = x ² отображает отрезок [ 1, 2] в отрезок [ 1,10] и на отрезок[ 1, 4]).

В этом семестре мы будем рассматривать действительнозначные функции одной действительной переменной, т.е. X Í R, Y Í R. Множество точек {(x, y)| x Î X, y = f (x)} на плоскости будем называть графиком функции y = f (x).

Обычно перечисляются следующие способы задания функции: аналитический, графический, табличный.

Введем важное определение суперпозиции функций:

Опр.4.1.2. Пусть даны функции j: Т ® Х и f: X ® Y. Функция F: Т ® Y, ставящее в соответствие элементу t Î T элемент у Î Y по правилу y = f (j(t)), называется суперпозицией функций f и j (или сложной функцией).

Так, функция y =sin(x ⁵) есть суперпозиция функций z = x ⁵ и y =sin(z).

Предполагается, что студенты знают свойства и графики основных элементарных функций (степенной y = x ^a; показательной y = a^x, a >0, a ¹1; логарифмической y = log _a x, a >0, a ¹1; тригонометрических y = sin x, y = cos x, y = tg x, y = ctg x; обратных тригонометрических y = arcsin x, y = arccos x, y = arctg x, y = arcctg x) и умеют строить эскизы графиков элементарных функций (функций, получающихся из основных элементарных с помощью конечного числа арифметических действий и суперпозиций). К основным функциям отнесём также гиперболические функции: синус гиперболический y = sh x, косинус гиперболический y = ch x, тангенс гиперболический y = th x, котангенс гиперболический y = cth x и обратные им арксинус гиперболический y = ar sh x, арккосинус гиперболический y = ar ch x, арктангенс гиперболический y = ar th x, арккотангенс гиперболический y = ar cth x, основные сведения о которых будут приведены ниже.

Примеры неэлементарных функций:

Функция Е(х) - целая часть х - наибольшее целое число, не превосходящее х (график справа);

Функция Дирихле:

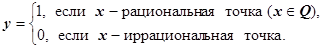
Функция Римана:

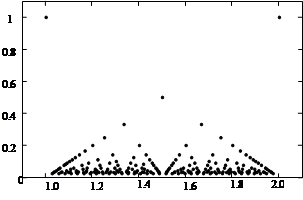График функции Римана на отрезке [1,2] качественно изображён справа (построены рациональные точки со знаменателями ). Основной факт, который очевиден из рисунка и который нам понадобится в дальнейшем – при любом e>0 выше линии у =e лежит не более чем конечное число точек графика.

Напомним терминологию, применяемую для описания свойств функций.

Опр.4.1.3. Функция называется ограниченной сверху на множестве Х, если существует такое число М, что для любого x Î X выполняется неравенство f (x)£ М.

В краткой форме записи: f (x) ограничена сверху на Х Û {$ М Î R " x Î Xf (x)£ М }.

Опр.4.1.4. f (x) ограничена снизу на Х Û {$ М Î R " x Î Xf (x)³ М }.

Опр.4.1.5. f (x) ограничена на Х Û {$ М Î R " x Î X | f (x)|£ М }. (Другими словами,

- М £ f (x)£ М, т.е. f (x) ограничена и сверху и снизу).

Опр.4.1.6. f (x) возрастает (не убывает) на Х Û {" x ₁, x ₂Î Xx ₁< x ₂ Þ f (x ₁)£ f (x ₂)}.

Опр.4.1.7. f (x) строго возрастает на Х Û {" x ₁, x ₂Î Xx ₁< x ₂ Þ f (x ₁)< f (x ₂)}.

Опр.4.1.8. f (x) убывает (не возрастает) на Х Û {" x ₁, x ₂Î Xx ₁< x ₂ Þ f (x ₁)³ f (x ₂)}.

Опр.4.1.9. f (x) строго убывает на Х Û {" x ₁, x ₂Î Xx ₁< x ₂ Þ f (x ₁)> f (x ₂)}.

Опр.4.1.10. f (x) монотонна на Х, если она или возрастает, или убывает на Х.

Опр.4.1.11. f (x) строго монотонна на Х, если она или строго возрастает, или строго убывает на Х.

Пусть дано отображение Х на Y: F: X ® Y. Обратным отображением F ^-1: Y ® X называется отображение, которое каждому элементу у Î Y ставит в соответствие тот элемент x Î X, для которого F (х) = у. Для того, чтобы обратное отображение было функцией, необходимо, чтобы этот элемент х определялся однозначно, т.е. чтобы прямое отображение F: X ® Y было взаимно-однозначным. Таким образом, для того, чтобы функция у = f (x) с областью определения X и областью значений Y = Y_f имела обратную функцию, необходимо и достаточно, чтобы она принимала разные значения в разных точках: x ₁¹ x ₂ Þ f (x ₁) ¹ f (x ₂). Формальное определение:

Опр.4.1.12. Пусть функция у = f (x) взаимно-однозначно отображает множество X на множество Y. Обратной к f (x) называется функция x = g (y) с областью определения Y и множеством значений X, которая каждому у Î Y ставит в соответствие тот элемент x Î X, для которого f (х) = у. Часто для обратной функции применяется обозначение x = f ^-1(y).

Очевидно, что 1. если g (y) обратна к f (x), то f (x) обратна к g (y) (т.е. эти функции взаимно обратны); 2. f (g (y)) = y, g (f (x)) = x. Очевидно также, что строгая монотонность функции обеспечивает существование обратной функции, при этом обратная функция тоже строго монотонна. Графики взаимно обратных функций симметричны относительно прямой y = x.

Опр.4.1.14. Функция у = f (x) называется чётной, если

1. её область определения симметрична относительно точки x = 0 (т.е. если x Î X, то и - x Î X);

2. для " x Î Xf (x) = f (- x).

Опр.4.1.14. Функция у = f (x) называется нечётной, если

1. её область определения симметрична относительно точки x = 0;

2. для " x Î Xf (x) = - f (- x).

Функции, не являющиеся ни чётными, ни нечётными, принято называть функциями общего вида.

Любую функцию, область определения которой симметрична относительно точки x = 0, можно единственным образом представить в виде суммы чётной и нечётной.

Опр. 4.1.15. Функция называется периодической, если существует число Т ¹0 такое, что для " x Î X: 1. x + Т Î X; 2. f (x + Т) = f (x). Число Т называется периодом функции.

Периодическими являются тригонометрические функции. Нетривиальные примеры: периодична любая постоянная функция f (x) = С =const; периодична функция Дирихле, причем её периодом может служить любое рациональное число. Из определения следует, что если Т - период функции, то числа 2 Т, 3 Т, …. - тоже периоды. Наименьший отличный от нуля положительный период называется основным периодом. Функция Дирихле демонстрирует пример периодической функции, не имеющей основного периода.

4.2. Гиперболические функции.

Дата добавления: 2014-01-11