
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства сходящейся последовательности
Сформулируем и докажем ряд свойств сходящейся последовательности (т.е. последовательности, имеющей предел).
4.3.2.1. Если последовательность постоянна (т.е. аn =const=C для " n), то она имеет предел, и этот предел равен числу С.
Док-во. Неравенство | аn -C |=0<e выполняется для " n,"e, т.е. выполняются условия определения предела.
4.3.2. 2. Последовательность может иметь только один предел.
Док-во. От противного: предположим, что последовательность имеет два предела:  и
и  . Предположим для определённости, что b > a. Возьмём в качестве e любое число, меньшее, чем (b - a)/2. Так как
. Предположим для определённости, что b > a. Возьмём в качестве e любое число, меньшее, чем (b - a)/2. Так как  , то, по определению предела последовательности, $ N 1: n > N 1 Þ a -e< an < a +e< a +(b - a)/2=(a + b)/2. Так как
, то, по определению предела последовательности, $ N 1: n > N 1 Þ a -e< an < a +e< a +(b - a)/2=(a + b)/2. Так как  , то $ N 2: n > N 2 Þ(a + b)/2= b -(b - a)/2< b -e< an < b +e. Возьмём N =max{ N 1, N 2}. Тогда при n > N одновременно должны выполняться неравенства an < (a + b)/2 и an > (a + b)/2, что невозможно.
, то $ N 2: n > N 2 Þ(a + b)/2= b -(b - a)/2< b -e< an < b +e. Возьмём N =max{ N 1, N 2}. Тогда при n > N одновременно должны выполняться неравенства an < (a + b)/2 и an > (a + b)/2, что невозможно.
4.3.2.3. Если последовательность сходится, то она ограничена.
Док-во. Пусть $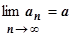 . Возьмём e=1. $ N: n > N Þ a -1< an < a +1. Итак, все члены последовательности, начиная с N +1, ограничены снизу числом a -1, сверху - числом a +1. Вне окрестности U 1(a) точки a может лежать не более N членов. Возьмём в качестве нижней границы число М 1=min{ a1, a2, a3,…, aN, a -1}, в качестве верхней границы число М 2=max{ a1, a2, a3,…, aN, a +1}. Тогда М 1
. Возьмём e=1. $ N: n > N Þ a -1< an < a +1. Итак, все члены последовательности, начиная с N +1, ограничены снизу числом a -1, сверху - числом a +1. Вне окрестности U 1(a) точки a может лежать не более N членов. Возьмём в качестве нижней границы число М 1=min{ a1, a2, a3,…, aN, a -1}, в качестве верхней границы число М 2=max{ a1, a2, a3,…, aN, a +1}. Тогда М 1 an
an  М 2, т.е. последовательность
М 2, т.е. последовательность 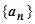 действительно ограничена.
действительно ограничена.
Обратное утверждение неверно. Последовательность  ограничена: 1
ограничена: 1 an <2, но предела не имеет (подпоследовательность членов с нечётными индексами сходится к числу 1, с чётными - к числу 2, последовательность в целом предела не имеет). Однако если мы дополнительно потребуем, чтобы последовательность была монотонной, то существование предела будет обеспечено:
an <2, но предела не имеет (подпоследовательность членов с нечётными индексами сходится к числу 1, с чётными - к числу 2, последовательность в целом предела не имеет). Однако если мы дополнительно потребуем, чтобы последовательность была монотонной, то существование предела будет обеспечено:
4.3.2.4. Если последовательность возрастает и ограничена сверху, то она сходится (т.е. имеет предел).
4.3.2.5. Если последовательность убывает и ограничена снизу, то она сходится.
Док-во. Докажем утверждение 4.3.2.4. (4.3.2.5 доказывается аналогично). Так как множество чисел 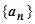 ограничено сверху, оно имеет точную верхнюю грань
ограничено сверху, оно имеет точную верхнюю грань  . По свойствам точной верхней грани 1. an
. По свойствам точной верхней грани 1. an  a; 2. для "e>0 существует элемент множества aN такой, что aN > a -e. Если n > N, то a -e< aN
a; 2. для "e>0 существует элемент множества aN такой, что aN > a -e. Если n > N, то a -e< aN  an (вследствие монотонного возрастания)
an (вследствие монотонного возрастания)  a < a +e. Итак, для "e>0 мы нашли такое N, что при n > N имеет место a -e< an < a +e, т.е. доказали, что $
a < a +e. Итак, для "e>0 мы нашли такое N, что при n > N имеет место a -e< an < a +e, т.е. доказали, что $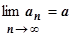 .
.
Приведём без доказательства ещё один факт, касающийся ограниченных последовательностей:
4.3.2.6. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Опр. 4.3.3. Последовательность называется фундаментальной, если она удовлетворяет следующему условию: для "e>0 существует число N такое, что для любых n1, n2 > N выполняется неравенство | an1 - an2 |<e.
4.3.2.7. Последовательность сходится тогда и только тогда, когда она фундаментальна.
Док-во. Необходимость. Пусть последовательность сходится, и её предел равен a. Возьмём "e>0. $ N: n > N Þ| a - an |< . Возьмём любые n1, n2 > N. Тогда и | a - an1 |<
. Возьмём любые n1, n2 > N. Тогда и | a - an1 |< , и
, и
| a - an2 |< . Оценим | an1 - an2 |: | an1 - an2 |=| an1 - a+a - an2 |=| (an1 - a)-(a n2 - a) |
. Оценим | an1 - an2 |: | an1 - an2 |=| an1 - a+a - an2 |=| (an1 - a)-(a n2 - a) |  | an1 - a | +
| an1 - a | +
+ | a n2 - a |< +
+ =e Þ последовательность
=e Þ последовательность 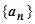 фундаментальна.
фундаментальна.
Достаточность строго доказывать не будем, приведём идею доказательства. Если последовательность фундаментальна, то она ограничена (доказывается аналогично свойству 4.3.2.3), следовательно из неё можно выделить подпоследовательность, сходящуюся к некоторому числу a. Далее показывается, что это число будет пределом всей последовательности 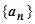 .
.
Далее будет сформулирован ряд свойств, касающихся арифметических действий с последовательностями и пределами. Эти свойства легко доказываются с применением бесконечно малых величин; мы докажем эти свойства позже, когда будем изучать пределы функций. Для функций также будет доказан ряд других свойств, справедливых и для последовательностей (теоремы о сохранении знака предела, о переходе к пределу в неравенстве и т.д.; см. пункт 4.4.4. Свойства функций, имеющих предел). Если даны последовательности 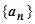 ,
, , то символом
, то символом 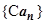 будем обозначать последовательность, получающуюся из
будем обозначать последовательность, получающуюся из 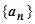 умножением всех её членов на постоянную величину С=const. Символами
умножением всех её членов на постоянную величину С=const. Символами  будем обозначать последовательности, получающиеся из
будем обозначать последовательности, получающиеся из 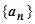 ,
, , соответственно, почленным сложением, умножением, делением исходных последовательностей. Тогда:
, соответственно, почленным сложением, умножением, делением исходных последовательностей. Тогда:
4.3.2.8. Если последовательность 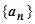 сходится, то сходится последовательность
сходится, то сходится последовательность 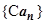 , и
, и
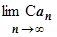 =С
=С (постоянный множитель можно выносить за знак предела);
(постоянный множитель можно выносить за знак предела);
4.3.2.9. Если последовательности 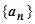 ,
,  сходятся, то сходятся и последовательности
сходятся, то сходятся и последовательности  , и
, и
4.3.2.10.  (предел суммы последовательностей равен сумме пределов);
(предел суммы последовательностей равен сумме пределов);
4.3.2.11.  (предел произведения последовательностей равен произведению пределов);
(предел произведения последовательностей равен произведению пределов);
4.3.2.12. 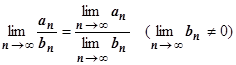 (предел частного последовательностей равен частному их пределов (при условии, что предел знаменателя отличен от 0)).
(предел частного последовательностей равен частному их пределов (при условии, что предел знаменателя отличен от 0)).
|
|
Дата добавления: 2014-01-11; Просмотров: 758; Нарушение авторских прав?; Мы поможем в написании вашей работы!