Для примера рассмотрим функцию

В точке х =0 эта функция не определена; найдём односторонние пределы при х ®±0. При х ®+0 (т.е. справа) (-1/ х) ®-µ, е^(-1/ х)®0, f (x) ®2+3/4=11/4. При х ®-0 (т.е. слева) (-1/ х) ®+µ, е^(-1/ х)® +µ, 3/(4+ е^(-1/ х)) ®0, f (x) ®2. Таким образом

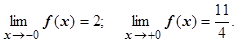Найдем пределы этой функции при х ®±µ. И при х ®-µ, и при х ®+µ получим (-1/ х) ®0, е^{(-1/ х)}®1, f (x) ®2+3/5=13/5.

Связь между пределом функции и односторонними пределами устанавливает

Теор. 4.4.1. Для того, чтобы существовал (или ), необходимо и достаточно, чтобы существовали и были равны односторонние пределы.

Док-во. Необходимость. Пусть $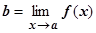. Для "e>0 $d: 0<| x - a |<d Þ| f (x)- b |<e. Но тогда | f (x)- b |<e и при 0< x - a <d(Þ0< x < a +d), и при -d< x - a <0(Þ a -d< x <0), т.е. выполняются условия определений , , следовательно, оба односторонние предела существуют и равны между собой.

Достаточность. Пусть $, $. Возьмём "e>0. Первый предел обеспечивает существование d₁: a < x < a +d₁Þ| f (x)- b |<e. Аналогично второй предел обеспечивает существование d₂: a -d₂< x <0Þ| f (x)- b |<e. Выберем d<min{d₁, d₂}. Тогда при 0<| x - a |<d для x > a будет выполняться первое неравенство, для всех x < a - второе. В обоих случаях | f (x)- b |<e, т.е. $, и этот предел равен числу b.

Задание 3. Самостоятельно сформулировать определение односторонних пределов на языке последовательностей. 4. Сформулировать условие отсутствия односторонних пределов.

4.4.3. Бесконечно большие функции.

Опр.4.4.8. Функция f(x) называется бесконечно большой при х ® а, если .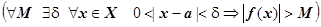

Обозначение: .

Опр.4.4.9. Функция f(x) называется положительной бесконечно большой при х ® а, если .

Опр.4.4.9. Функция f(x) называется отрицательной бесконечно большой при х ® а, если .

Такие же определения даются для случаев х ® а +0, х ® а -0, х ®+¥, х ®-¥.

Пример: 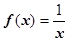бесконечно большая при х ®0, положительная бесконечно большая при х ®+0, отрицательная бесконечно большая при х ®-0. Коротко эти свойства записываются с применением символики пределов так: , , . Тем не менее, когда мы в дальнейшем будем говорить "пусть f (x) имеет предел при 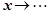", всегда будем предполагать, что этот предел конечен (противный случай будет специально подчёркиваться).

Если функция бесконечно большая, то она очевидно не ограничена. Но не всякая неограниченная функция - бесконечно большая. На графике справа изображена функция на отрезке [0.01, 0.1]. Эта функция неограничена на полуинтервале (0,1] (знаменатель ®0), но в любой окрестности точки 0 имеются точки, в которых f (x)=0, т.е. f (x) не бесконечно большая.

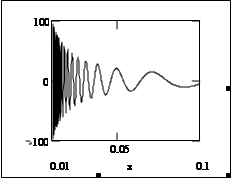Для бесконечно больших функций будем применять аббревиатуру ББ.

Задание. 6. Самостоятельно перебрать все возможные варианты определений ББ (положительных ББ, отрицательных ББ) при х ® а +0, х ® а -0, х ®+¥ и т.д. Сформулировать эти определения на языке последовательностей.

4.4.4. Свойства функций, имеющих предел.

Теор. 4.4.2 (о единственности предела). Если функция имеет предел при х ® а, то этот предел единственен.

Док-во от противного. Пустьфункция имеет два предела при х ® а: b ₁ и b ₂, b ₁¹ b ₂, пусть b ₂> b ₁. Возьмём e<(b ₂- b ₁ )/2. $d₁: 0<| x - a |<d₁ Þ| f (x)- b ₁ |<eÛ-e< f (x)- b ₁<eÛ b ₁-e< f (x)< b ₁+eÞ f (x)< b ₁+e< b ₁+(b ₂- b ₁ )/2=(b ₁+ b ₂ )/2. Аналогично $d₂: 0<| x - a |<d₂ Þ| f (x)- b ₂ |<eÛ-e< f (x)- b ₂<eÛ b ₂-e< f (x)< b ₂+eÞ f (x)> b ₂-e> b ₂-(b ₂- b ₁ )/2=(b ₁+ b ₂ )/2. Таким образом, при

0<| x - a |<min{d₁,d₂}должно быть одновременно f (x)< (b ₁+ b ₂ )/2 и f (x)> (b ₁+ b ₂ )/2, что невозможно - получено противоречие.

Теор. 4.4.3 (о локальной ограниченности функции, имеющей предел). Если функция имеет предел b при х ® а, то она ограничена в некоторой окрестности точки а.

Док-во. Возьмём e=1. $d: 0<| x - a |<d Þ| f (x)- b |<1Þ -1< f (x)- b <1Þ b -1< f (x)< b +1Þв d-окрестности точки аf (x) ограничена сверху и снизу Þона в этой окрестности ограничена.

Теор. 4.4.4 (о сохранении функцией знака предела). Если функция имеет предел b при х ® а, и число b >0 (либо b <0), то существует окрестность точки а, в которой f (x)>0 (либо f (x)<0).

Док-во. Рассмотрим для определённости случай b >0. Возьмём e= b /2. $d: 0<| x - a |<d Þ| f (x)- b |< b /2Þ - b /2< f (x)- b < b /2Þ b - b /2< f (x)< b + b /2Þ f (x)> b /2>0, что и требовалось доказать.

Очевидные следствия: 1. Если b > B, то f (x)> B в некоторой окрестности предельной точки; 2. Если f (x)>0 в некоторой окрестности предельной точки, то не может быть b <0.

Теор. 4.4.5 (о переходе к пределу в неравенстве). Если в некоторой окрестности точки а функции f (x), g (x) удовлетворяют неравенству f (x)£ g (x) и имеют пределы при х ® а, то и их пределы удовлетворяют неравенству .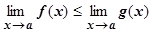

(Напомним, что когда мы говорим о некоторых свойствах функций, имеющих предел, в окрестности предельной точки, то подразумеваем, что эти свойства выполняются во всех точках этой окрестности, за исключением, возможно, самой предельной точки. Значение функции в предельной точке никак не участвует в определении предела и вообще может не существовать).

Док-во от противного. Пусть 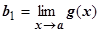, , и пусть b ₁< b ₂. Возьмём

e<(b ₂- b ₁ )/2. $d₂: 0<| x - a |<d₂ Þ| f (x)- b ₂ |<eÛ-e< f (x)- b ₂<eÛ b ₂-e< f (x)< b ₂+eÞ f (x)> b ₂-e> b ₂-(b ₂- b ₁ )/2=(b ₁+ b ₂ )/2. Аналогично $d₁: 0<| x - a |<d₁ Þ| g (x)- b ₁ |<eÛ- e< g (x)- b ₁<eÛ b ₁-e< g (x)< b ₁+eÞ g (x)< b ₁+e< b ₁+(b ₂- b ₁ )/2=(b ₁+ b ₂ )/2. Таким образом, при 0<| x - a |<min{d₁,d₂}должно быть f (x)> (b ₁+ b ₂ )/2, g (x)< (b ₁+ b ₂ )/2 что противоречит условию f (x)£ g (x).

Теор. 4.4.6 (о пределе промежуточной функции). Если в некоторой окрестности точки а функции f (x), g (x), h (x) удовлетворяют неравенству f (x)£ g (x) £ h (x), функции f (x), h (x) имеют пределы при х ® а, и эти пределы равны: , то и функция g (x) имеет предел при х ® а, и этот предел тоже равен числу b.

Док-во. $d₁: 0<| x - a |<d₁ Þ| f (x)- b |<eÛ -e< f (x)- b <eÛ b -e< f (x)< b +eÞ f (x)> b -e. $d₂:

0<| x - a |<d₂ Þ| h (x)- b ₂ |<eÛ -e< h (x)- b <eÛ b -e< h (x)< b +eÞ h (x)< b+ e. Таким образом, при

0<| x - a |<min{d₁,d₂}=d будет b -e< f (x)£ g (x) £ h (x) < b+ eÞ| h (x)- b |<e, т.е. g (x) имеет предел, равный числу b.

Задание. Утверждения этого раздела сформулированы для случая х ® а. Самостоятельно сформулировать и доказать их для других случаев (односторонних пределов, пределов на бесконечности).

4.4.5. Бесконечно малые (БМ) функции.

Опр. 4.4.10. Функция f (x) называется бесконечно малой при х ® a, если .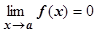

БМ функции принято обозначать греческими буквами:a(х), b(х) и т.д, так и будем делать. Перевод определения на язык e-d:

a(х) - БМ при х ® a Û {"e>0 $d: 0<| x - a |<dÞ|a(х)|<e}.

БМ обладают всеми свойствами функций, имеющих предел. В этом разделе мы изучим специфические свойства БМ.

Теор. 4.4.7. Произведение БМ на ограниченную функцию - БМ функция.

Док-во. Пусть a(х) - БМ при х ® a, f (x) ограничена в окрестности точки a. Требуется доказать, что a(х) f (x) - БМ при х ® a. $С>0: | f (x) |<C; "e>0 $d: 0<| x-a |<dÞ|a(х)|<e/CÞ

| a(х) f (x)|<e, т.е. a(х) f (x) действительно БМ при х ® a.

Теор. 4.4.8. Алгебраическая сумма конечного числа БМ функций - БМ функция.

Док-во. Пусть a(х), b(х) - БМ при х ® a. Требуется доказать, что a(х) ±b(х) - БМ при х ® a. "e>0 $d₁: 0<| x-a |<d₁Þ|a(х)|<e/2; $d₂: 0<| x-a |<d₂Þ|b(х)|<e/2. Если взять 0<| x-a |<min{d₂,d₁}=d, то | a(х) ±b(х)|£ | a(х) |+ | b(х)|< e/2+e/2=e, т.е. a(х) ±b(х) действительно БМ при х ® a.

Следствие: Линейная комбинация БМ функций - БМ функция.

Докажем теорему, которой придётся часто пользоваться и которая, в основном, объясняет причину выделения БМ функций в отдельный класс:

Теор. 4.4.9 (о связи функции с её пределом). Для того, чтобы функция f (x) имела предел, равный b, при х ® a, необходимо и достаточно, чтобы f (x) представлялась в виде f (x)= b +a(х), где a(х) - БМ при при х ® a.

Док-во. Необходимость. Пусть $. Обозначим a(х)= f (x) - b, докажем, что a(х) - БМ при при х ® a. По определению предела "e>0 $d: 0<| x - a |<dÞ| f (x) - b |=|a(х)|<e, т.е. a(х) удовлетворяет определению БМ.

Достаточность. Для доказательства достаточно прочитать доказательство необходимости в противоположном порядке.

Дата добавления: 2014-01-11