
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сравнение поведения функций при х®а. Главная часть функции
|
|
|
|
Здесь мы определим символику, которая применяется в математической и технической литературе для сравнительного описания поведения функций вблизи предельной точки.
Определения. 4.4.8.1. f (x)~ g (x) (f (x) эквивалентна g (x)) при х ® а, если f (x)= s (x) g (x), где s (x)®1 при х ® а. Если g (x)¹0 в окрестности точки а, то f (x)~ g (x), если  =1.
=1.
В остальных определениях мы не будем писать х ® а, но это везде подразумевается. Всё, что будет рассматриваться, верно и в случаях х ® а -0, х ® а +0 и т.д. В скобках будут даваться равносильные определения для случая, когда g (x)¹0 в окрестности точки а.
4.4.8.2. f (x)=О(g (x)) (О большое от g (x)), если f (x)= s (x) g (x), где s (x) ограничена в некоторой окрестности точки а. (f (x)=О(g (x)), если отношение f (x)/ g (x) ограничено в окрестности точки а.)
4.4.8.3. f (x)=о(g (x)) (О малое от g (x)), если f (x)= a(x) g (x), где a(x) - БМ функция. (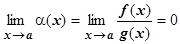 .)
.)
4.4.8.4. f (x)=О(1) - функция, ограниченная в некоторой проколотой окрестности точки а.
4.4.8.5. f (x)=о(1) - БМ функция (f (x) ®0 при х ® а.)
Перечислим ряд очевидных свойств введённых отношений (обязательно осмыслить!).
4.4.8.1. Если f (x)~ g (x), то g (x)~ f (x).
4.4.8.2. Если f (x)~ g (x), g (x)~ h (x), то f (x)~ h (x).
4.4.8.3. Если f (x)~ g (x), h (x)~ s (x), то f (x) h (x)~ g (x) s (x).
4.4.8.4. Если  , то f (x)~ L.
, то f (x)~ L.
4.4.8.5. Если f (x)=o(g (x)), то f (x)=O(g (x)).
4.4.8.6. Если f (x)~ g (x), то o(f (x))=o(g (x)).
4.4.8.7. O(O(f (x)))= O(f (x)); O(o(f (x)))= o(O(f (x)))= o(f (x)); o(o(f (x)))= o(f (x)).
4.4.8.8. g (x)(O(f (x)))= O(g (x) f (x)); g (x)(o(f (x)))= o(g (x) f (x)).
4.4.8.9. O(f (x)) O(f (x))= O(f 2 (x)); O(f (x)) o(f (x))= o(f 2 (x)); o(f (x)) o(f (x))= o(f 2 (x)).
4.4.8.10. O(f (x))+O(f (x))= O(f (x)); O(f (x))+o(f (x))= O(f (x)); o(f (x))+o(f (x))= o(f (x)).
4.4.8.11. Из этих свойств и теоремы 4.4.10.2 о пределе разности функций следует:
f (x)~ g (x)Û f (x)- g (x)=о(f (x)); f (x)~ g (x)Û f (x)- g (x)=о(g (x)).
Условие f (x)~ g (x)Û f (x)- g (x)=о(g (x)) можно записать так: f (x)~ g (x)Û f (x)= g (x)+о(g (x)).
Опр. 4.4.8.6. Если функцию f (x) можно представить в виде f (x)= g (x)+о(g (x)), то функция g (x) называется главной частью функции f (x).
|
|
|
4.4.9. Сравнение бесконечно малых функций.
В предыдущем разделе введены определения, описывающие поведение при х ® а произвольных функций. Здесь мы уточним эти определения для случая бесконечно малых функций. Поведение БМ функций сравнивается, если существует конечный или бесконечный предел их отношения. Итак, пусть a(х)®0, b(х)®0 при х ® а и пусть $ .
.
Опр. 4.4.9.1. Если  - конечное число, отличное от нуля, то БМ функции a(х) и b(х) называются бесконечно малыми одного порядка.
- конечное число, отличное от нуля, то БМ функции a(х) и b(х) называются бесконечно малыми одного порядка.
Опр. 4.4.9.2. Если  =0, то БМ a(х) называется бесконечно малой более высокого порядка по сравнению с b(х) (b(х) называется бесконечно малой низшего порядка по сравнению с a(х)). Обозначение: a(х) = о(a(х)).
=0, то БМ a(х) называется бесконечно малой более высокого порядка по сравнению с b(х) (b(х) называется бесконечно малой низшего порядка по сравнению с a(х)). Обозначение: a(х) = о(a(х)).
Опр. 4.4.9.3. Если  =1, то БМ a(х) и b(х) называются эквивалентными. Обозначение: a(х)~b(х); если a(х)~b(х), то b(х)~a(х).
=1, то БМ a(х) и b(х) называются эквивалентными. Обозначение: a(х)~b(х); если a(х)~b(х), то b(х)~a(х).
Эквивалентные БМ интенсивно используются и в теории, и при решении задач, поэтому докажем два утверждения об этих величинах.
Теор. 4.4.9.1. (Необходимое и достаточное условие эквивалентности БМ). Для того, чтобы БМ функции были эквивалентными, необходимо и достаточно, чтобы их разность была БМ функцией высшего порядка по сравнению с каждой из них.
Док-во. Необходимость. a(х)~b(х)Û =1Û
=1Û 0Û
0Û 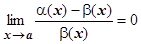 . Достаточность.
. Достаточность. 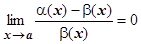 Û
Û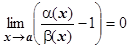 Û
Û  =1.
=1.
Теор. 4.4.9.2 о замене бесконечно малых на эквивалентные.
Пусть a(х)~ a1(х), b(х)~b1(х) - БМ функции. Тогда  .
.
Док-во. 
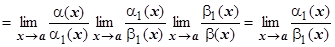 .
.
Опр. 4.4.9.4. Если  при некотором k>0, то БМ a(х) называется БМ
при некотором k>0, то БМ a(х) называется БМ
k-го порядка малости по сравнению с b(х).
Если a(х) - БМ к-го порядка по сравнению с b(х), то a(х)~C[b(х)]kÞa(х)=C[b(х)]k+o(a(x)), т.е. функция C[b(х)]k - главная часть функции a(х). В этом случае также a(х)=C[b(х)]k+o([b(х)]k).
При решении задач часто применяется следующее очевидное
Утверждение. Сумма конечного числа БМ функций разных порядков эквивалентна слагаемому низшего порядка.
4.4.10. Таблица эквивалентных бесконечно малых.
Здесь мы с помощью рассмотренных в 4.4.7 пределов составим таблицу эквивалентных БМ функций и выпишем следующие из них выражения для главных частей (они подчёркнуты).
|
|
|
| Эквивалентность при х ®0 | Главная часть при х ®0 |
| 1. sin x ~ x | 1. sin x = x +o(x) |
| 2. 1 - cos x ~ x 2/2 | 2. 1 - cos x = x 2/2 +o(x 2)Þcos x = 1- x 2/2+o(x 2) |
| 3. tg x ~ x | 3. tg x = x +o(x) |
| 4. arcsin x ~ x | 4. arcsin x = x +o(x) |
| 5. arctg x ~ x | 5. arctg x = x +o(x) |
| 6. ax -1 ~ x ln a; ex -1 ~ x | 6. ax –1 = x ln a +o(x)Þ ax = 1+ x ln a +o(x) ex –1 = x +o(x))Þ ex = 1+ x +o(x) |
| 7. log a (1+ x) ~ x log a e; ln(1+ x) ~ x | 7. log a (1+ x) = x log a e +o(x); ln(1+ x) = x +o(x) |
| 8. (1+ x) a -1 ~ ax | 8. (1+ x) a - 1 = a x +o(x)Þ (1+ x) a =1 + a x +o(x) |
| 9. sh x ~ x | 9. sh x = x +o(x) |
| 10. ch x - 1 ~ x 2/2 | 10. ch x - 1= x 2/2 +o(x 2)Þ ch x = 1 + x 2/2+o(x 2) |
4.4.11. Бесконечно большие функции. Сравнение бесконечно больших функций и связь с бесконечно малыми функциями.
В разделе 4.4.3 мы определили функции ББ, положительные ББ, отрицательные ББ и ввели обозначения:  ,
,  ,
,  . Напомним одно из них.
. Напомним одно из них.
Опр.4.4.8. f (x)®¥ при х ® а (х ® а +0, х ® а -0, х ®¥, х ®+¥, х ®-¥) Û Û .
.
Теор. 4.4.11.1 о связи ББ и БМ функций. Пусть функции F (x) и j(x) связаны соотношением F (x)= . F (x) - ББ тогда и только тогда, когда j(x) -БМ.
. F (x) - ББ тогда и только тогда, когда j(x) -БМ.
Док-во. Необходимость. Пусть F (x) - ББ, докажем, что 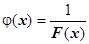 - БМ. Возьмём "e>0. По определению ББ, для М =1/e $d: 0<| x - a |<dÞ| F (x) |> М. Тогда
- БМ. Возьмём "e>0. По определению ББ, для М =1/e $d: 0<| x - a |<dÞ| F (x) |> М. Тогда  , т.е. j(x) удовлетворяет определению БМ.
, т.е. j(x) удовлетворяет определению БМ.
Достаточность доказывается аналогично необходимости.
Итак, связь между ББ и БМ функциями достаточно простая. Поэтому кратко перечислим факты, относящиеся к сравнению ББ функций и аналогичные определениям и теоремам для БМ.
Опр. 4.4.11.1. Если 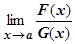 - конечное число, отличное от нуля, то ББ функции F (х) и G (х) называются бесконечно большими одного порядка роста при х ® а.
- конечное число, отличное от нуля, то ББ функции F (х) и G (х) называются бесконечно большими одного порядка роста при х ® а.
Опр. 4.4.11.2. Если 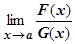 =0, то ББ G (х) называется бесконечно большой более высокого порядка по сравнению с F (х) (F (х) называется бесконечно большой низшего порядка по сравнению с G (х)). Обозначение: F (x) = o(G (x)).
=0, то ББ G (х) называется бесконечно большой более высокого порядка по сравнению с F (х) (F (х) называется бесконечно большой низшего порядка по сравнению с G (х)). Обозначение: F (x) = o(G (x)).
Опр. 4.4.11.3. Если 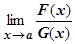 =1, то ББ G (х) и F (х) называются эквивалентными.
=1, то ББ G (х) и F (х) называются эквивалентными.
Теор. 4.4.11.2. (Необходимое и достаточное условие эквивалентности ББ). Для того, чтобы ББ функции F (х) и G (х) были эквивалентными, необходимо и достаточно, чтобы выполнялось условие F (х) - G (х) = о(F (х)) (или F (х) - G (х) = о(G (х)).
4.5. Решение задач на вычисление пределов.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 630; Нарушение авторских прав?; Мы поможем в написании вашей работы!